在实际中常遇到下面的问题：已知产品的某一质量指标服从正态分布，但由于原料、设备条件、操作人员不同，或工艺过程的改变等因素，引起总体均值、总体方差有所改变，我们需要知道这些变化有多大．这就需要考虑两个正态总体均值差或方差比的估计问题．
设总体X～N（μ1，σ21），Y～N（μ2，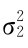
），且X与Y相互独立，X1，X2，…，Xn来自X的一个样本，Y1，Y2，…，Yn为来自Y的一个样本，对给定置信水平为1－α，且设X，Y， 
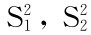分别为总体X与Y的样本均值与样本方差．
1．求μ1－μ2的置信区间
（1）当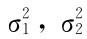
已知时，由抽样分布可知
所以可以得到μ1－μ2的置信水平为1－α的置信区间为
（2）当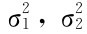
未知时，但m，n均较大（大于50），可用
分别代替
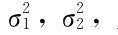则可得（μ1－μ2）的置信水平为1－α的近似置信区间为
（3）当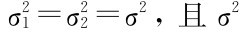
未知时，由抽样分布可知
若令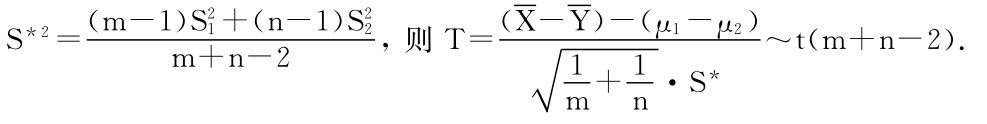
由t分布分位数的定义有：P｛｜T｜≤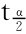
（m＋n－2）｝＝1－α，从而可得：μ1－μ2的可信度为1－α的置信区间为：
例7．3．6 为比较Ⅰ，Ⅱ两种型号步枪子弹的枪口速度，随机的取Ⅰ型子弹10发，得到枪口平均速度为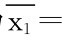
500（m／s），标准差s1＝1．10（m／s），取Ⅱ型子弹20发，得到枪口平均速度为
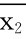＝496（m／s），标准差s2＝1．20（m／s），假设两总体都可认为近似地服从正态分布，且由生产过程可认为它们的方差相等，求两总体均值差μ1－μ2的置信度为0．95的置信区间．
解 由题设：两总体的方差相等，却未知，所以由（3）知
由于1－α＝0．95，α／2＝0．025，m＝10，n＝20，m＋n－2＝28，t0．075（28）＝2．0484，
故所求置信区间为：
＝4±0．93，即：（3．07，4．93）．
在该题中所得下限大于0，在实际中，我们认为μ1比μ2大，相反，若下限小于0，则认为μ1与μ2没有显著的差别．
2．μ1，μ2均未知时，求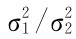
的置信区间
据抽样分布知：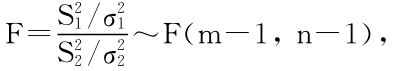
由F分布的分位数定义及其特点：
可得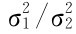
的置信水平为1－α的置信区间为：
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
