正态总体均值μ的假设检验

1．σ2已知，μ的假设检验（U－检验法）

（1）检验假设：H0：μ＝μ0，H1：μ≠μ0（双侧检验）

由于σ2已知，选统计量

在H0成立时，统计量U（又称为U统计量）服从标准正态分布，既U～N（0，1）．

在例8．1．1的分析中我们知道，检验的拒绝域为：W＝｛U＞｝．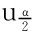

例8．2．1 某糖厂用自动包装机进行包糖，要求每袋0．5公斤，假定该机器包装重量X～N（μ，0．0152），现从生产线上随机取九袋乘重得X＝0．509，问该包装机生产是否正常？

解 由题意有包装机装糖重量X～N（μ，0．0152），要检验假设

由于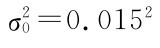已知，可用U－检验，取显著水平α＝0．05，查标准正态分布表有上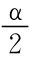分位数zα／2＝z0．0255＝1．96，而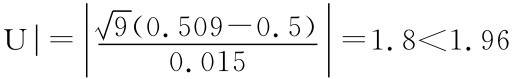没有落入拒绝域W内，故接受原假设，即认为包装机生产正常．

上述这种假设，其备择假设H1：μ≠μ0表明期望值μ可能大于μ0，也可能小于μ0，我们称这种检验为双侧检验．

（2）检验假设：H0：μ≤μ0，H1：μ＞μ0（单侧检验）

有时，我们只关心总体的期望是否增大，如产品的质量、材料的强度、元件的使用寿命等是否随着工艺改革而比以前提高，此时需检验假设H0：μ≤μ0，H1：μ＞μ0，还有一些问题，如新工艺是否降低了产品中的次品数，此时要检验假设H0：μ≥μ0，H1：μ＜μ0，像这种备择假设H1：μ＞μ0（或μ＜μ0）表示期望值只可能大于μ0（或只能小于μ0），这种检验称为单侧检验．对于单侧检验，最终得到的拒绝域的形式又如何呢？下面以假设H0：μ≤μ0，H1：μ＞μ0为例给予讨论：

当σ2为已知时，仍用U－检验．统计量U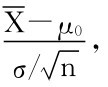＝只有当H1：μ＞μ0成立时有变大的趋势，因此，对于给定的显著性水平α，该检验的拒绝域应取为

W＝｛U＞zα｝．

同理，对于假设H0：μ≥μ0，H1：μ＜μ0在给定的显著性水平α，该检验的拒绝域应取为W＝｛U＜－zα｝．

例8．2．2 设某电子产品平均寿命5000小时为达到标准，现从一大批产品中抽出12件试验结果如下：5059，3897，3631，5050，7474，5077，4545，6279，3532，2773， 7419，5116．

假设该产品的寿命X～N（μ，1400），试问此批产品是否合格？

解 由题意可知该产品寿命X～N（μ，1400），要检验假设H0：μ≥5000↔H1：μ＜5000，

计算知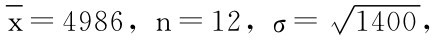则U＝＝－1．296，取α＝0．05，查得zα＝μ0．05＝1．645，拒绝域W＝｛U＜－zα｝，而此时－1．296＞－1．645，故可接受H0，即认为该批产品合格．

2．σ2未知，μ的假设检验（T—检验）

（1）检验假设：H0：μ＝μ0↔H1：μ≠μ0（双侧检验）

现在总体方差σ2未知，U－检验不能使用，由于样本方差S2是σ2的无偏估计量，故考虑用样本方差S2代替σ2，因此选取检验统计量

在H0成立时，T服从自由度为n－1的t分布，即T～t（n－1）．

与例题8．1．1分析类似，T不能太大，即 T太大是一个小概率事件．若给定的显著性水平α，查t分布表可得tα／2，使P｛T＞tα／2（n－1）｝＝α，从而得检验的拒绝域为W＝｛T＞－tα／2（n－1）｝，即W＝｛T＜－tα／2（n－1）或T＞tα／2（n－1）｝．

（2）单侧检验

类似地，对于单侧检验我们有如下结论：

（ⅰ）H0：μ≤μ0↔H1：μ＞μ0，其检验的拒绝域为W＝｛T＞tα（n－1）｝

（ⅱ）H0：μ≥μ0↔H1：μ＜μ0，其检验的拒绝域为W＝｛T＜－tα（n－1）｝

例8．2．3 化肥厂用自动包装机包装化肥，某日随机抽取9包，测得质量（单位：kg）如下：

49．7　 49．8　 50．3　 50．5　 49．7　 50．1　 49．9　 50．5　 50．4

若每包化肥的质量服从正态分布，问是否可以认为这天每包化肥的平均质量为50 （kg）？（取显著性水平α＝0．05）

解 设每包化肥质量为X，则X～N（μ，σ2），μ0＝50，σ2未知．

根据题意得到如下假设：H0：μ＝50↔H1：μ≠50，由于σ2未知，故采用T－检验，

计算知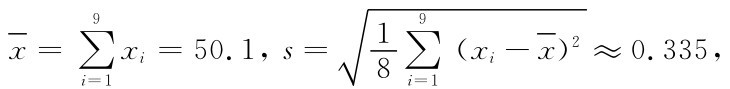对显著性水平α＝0．05，查表得 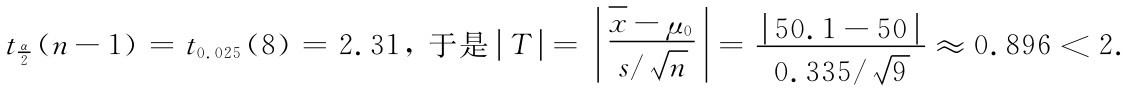31＝t0．025（8），于是接受H0，拒绝H1．即认为这天每包化肥的平均质量为50（kg）．

例8．2．4 已知某炼铁厂的铁水含碳量X服从正态分布，均值μ＝4．40．某日随机测得7炉铁水，算得平均含碳量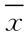＝4．51，标准差s＝0．11．以显著性水平α＝0．05检验这天铁水含碳量的均值是否显著提高？

解 这里μ0＝4．40，σ2未知，根据题意得到如下假设：

H0：μ＝4．40↔H1：μ＞4．40，

由于σ2未知，故采用T－检验，

由于＝4．51，标准差s＝0．11，对显著性水平α＝0．05，查表得tα（n－1）＝t0．05（6）＝1．943，

于是拒绝H0，接受H1，即认为这天该厂铁水含碳量的均值显著提高．