【摘要】：在以上的讨论中，我们假定Y关于x的回归函数μ（x）具有形式β0＋β1x，在处理实际问题时，μ（x）是否为x的线性函数，首先要根据有关专业知识和实践来判断，其次就要根据实际观察得到的数据运用假设检验的方法来判断．这就是说，求得的线性回归方程是否具有实用价值，一般来说，需要经过假设检验才能确定．若μ（x）为线性函数符合实际，则β1不应为零，因为若β1＝0，则μ（x）就不依赖于x了．因此，我们需要检验假
在以上的讨论中，我们假定Y关于x的回归函数μ（x）具有形式β0＋β1x，在处理实际问题时，μ（x）是否为x的线性函数，首先要根据有关专业知识和实践来判断，其次就要根据实际观察得到的数据运用假设检验的方法来判断．这就是说，求得的线性回归方程是否具有实用价值，一般来说，需要经过假设检验才能确定．若μ（x）为线性函数符合实际，则β1不应为零，因为若β1＝0，则μ（x）就不依赖于x了．因此，我们需要检验假设H0：β1＝0↔H1：β1≠0．
用t检验法来进行检验，可以证明：
且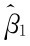
与Qe相互独立，故有
即
其中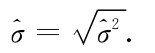
当H0为真时β1＝0，此时
且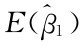
＝β1＝0，即得H0的拒绝域为
此处α为显著性水平．
当假设H0被拒绝时，认为回归效果是显著的，反之，就认为回归效果不显著．回归效果不显著的原因可能有如下几种：
（1）影响Y的取值，除了x及随机误差外还有其他不可忽略的因素；
（2）μ（x）不是x的线性函数，而是其他形式的函数；
（3）Y与x不存在关系．
例9．3 检验例9．1中回归方程的回归效果是否显著，取α＝0．05．
解 由例9．1和例9．2知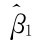
＝0．48303，Sxx＝8250，＾σ2＝0．9．查表得
t0．05／2（n－2）＝t0．025（8）＝2．3060，
则假设H0：β1＝0的拒绝域为
现在
故拒绝H0：β1＝0，认为回归效果是显著的．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
