2 一元函数微分学
17世纪机械制造、远洋航海、气象观测等大量实际问题激起了科学家们的研究兴趣,其中求变速运动的瞬时速度、曲线在某点的切线等问题的研究导致了微分学的产生,这些问题都归结为研究变量变化的快慢程度即变化率的问题.牛顿、莱布尼兹从不同的问题出发都用极限方法来研究问题,得出导数与微分这两个微分学的基本概念及计算,导数概念揭示了函数在瞬间变化的快慢程度,微分是用来表示函数在局部性质的重要数学工具,利用它们可以解决几何、物理以及工程技术中许多相关问题.本章主要研究一元函数的导数、微分的概念及其运算法则.
2.1 导数的概念
2.1.1 导数的概念
1) 几个实际问题
(1) 平面曲线的切线问题
设点M0(x0,y0)与M(x,y)分别是平面曲线y=f(x)上的一个定点与动点,则割线MM0的斜率为
![]()
根据切线的定义可知,当M→M0,即Δx→0时,若![]() 存在,则该极限就等于切线的斜率,即
存在,则该极限就等于切线的斜率,即
![]()
因此曲线y=f(x)在点M0(x0,y0)处的切线方程为
y-y0=k(x-x0)
(2) 变速直线运动的瞬时速度问题
设质点M沿某直线作s=s(t)的变速直线运动,s(t)为t时刻质点M所经过的路程,在时间段[t0,t]内,质点运动的平均速度为
![]()
当Δt越小,![]() (t)就越接近t0时刻的瞬时速度v(t0),所以平均速度的极限就是t0时刻的瞬时速度v(t0),即
(t)就越接近t0时刻的瞬时速度v(t0),所以平均速度的极限就是t0时刻的瞬时速度v(t0),即
![]()
(3) 边际成本问题
设C=f(x)表示产品生产或销售的某种成本函数,x为产品数量,若生产或销售的产品数量从x0增加到x0+Δx,则相应增加的成本为ΔC=f(x0+Δx)-f(x0).因此![]() 表示产品数量从x0增加到x0+Δx时的成本提高的平均速度,Δx越小,则
表示产品数量从x0增加到x0+Δx时的成本提高的平均速度,Δx越小,则![]() 就越接近x0时刻生产或销售成本提高的瞬时速度,因此
就越接近x0时刻生产或销售成本提高的瞬时速度,因此
![]()
表示产品数量为x0时,生产或销售成本提高的瞬时速度.其意义即在生产或销售的产品数量为x0时,每增加1个产品所需增加的成本,这在经济学中称为边际成本.
2) 导数的定义
从以上几个实际问题中可以看出,三类问题的实际意义虽各不相同,但摆脱所有的实际含义后,其数量关系相同,本质上都是求已知函数在一点处的函数增量与自变量增量的比值的极限,此极限表示函数在该点处的瞬时变化率,我们称之为导数.
在自然科学与工程技术领域中,还有许多关于瞬时变化率的问题,从这些问题中抽象出它们在数量关系上的共性,得到导数的定义.
定义1 设函数y=f(x)在x0的某个邻域内有定义,当自变量在这个邻域内从x0变到x0+Δx(Δx≠0)时,相应地函数有增量Δy=f(x0+Δx)-f(x0),如果极限![]() 存在,则称函数y=f(x)在点x0处可导,并称此极限为函数f(x)在x0处的导数,记作
存在,则称函数y=f(x)在点x0处可导,并称此极限为函数f(x)在x0处的导数,记作![]() 或
或![]() ,即
,即
![]()
(2-1)
在定义1中,若记x=x0+Δx,则(2-1)式可写成
![]()
(2-2)
当式(2-1)或(2-2)中的极限不存在时,则称函数f(x)在x0处不可导.
若函数f(x)在x0处不可导的原因是![]() =∞,为了方便起见,也说f(x)在x0处的导数为无穷大,记作f′(x0)=∞.
=∞,为了方便起见,也说f(x)在x0处的导数为无穷大,记作f′(x0)=∞.
由导数定义可知,前面三个实际问题的结果可表示为:
① 曲线y=f(x)在点(x0,f(x0))处的切线的斜率为k=f′(x0);
② 变速直线运动s=s(t)在时刻t0处的瞬时速度为v(t0)=s′(t0);
③ 生产或销售成本函数为C=f(x)时,在生产或销售的产品数为x0时的边际成本为f′(x0).
下面利用导数定义讨论一些简单函数的导数或可导性.
例1 设f(x)=x3,证明:∀x0∈R,有![]() .
.
证 ∀x0∈R,
![]()
![]()
所以
![]()
![]()
即
![]()
例2 讨论函数![]() 在x=0处的可导性.
在x=0处的可导性.
解 在x=0处,由于

所以
![]()
即该函数在x=0处不可导.
下面利用函数左、右极限的定义,得出相应函数的左、右导数的定义.
定义2 如果右极限
![]()
存在,则称此右极限为函数y=f(x)在x0处的右导数,记作![]() +(x0),即
+(x0),即
![]()
类似地,如果左极限
![]()
存在,则称此左极限为函数y=f(x)在x0处的左导数,记作![]() -(x0),即
-(x0),即
![]()
由极限存在的充要条件可知函数y=f(x)在x0处可导的充要条件为f(x)在x0处的左、右导数存在且相等.
常利用上述充要条件讨论分段函数在分段点处的可导性.
例3 设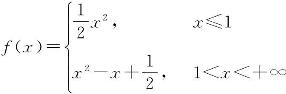 ,讨论f(x)在x=1处的可导性,若可导,求f′(1).
,讨论f(x)在x=1处的可导性,若可导,求f′(1).
解 在x=1处,![]() ,由
,由


即![]() (1)=1,故f(x)在x=1处可导,且f′(1)=1.
(1)=1,故f(x)在x=1处可导,且f′(1)=1.
例4 讨论函数f(x)=|x|在x=0处的可导性.
解 由
![]()
![]()
即
![]()
故f(x)在x=0处不可导.
利用函数的导数定义也可以解决一类特殊的函数极限问题.
例5 设f(x)在x0处可导,求![]() .
.
解 由题设可知
![]()
令Δx=-h,则
![]()
所以
![]()
下面给出函数在区间上可导的定义.
定义3 (1) 如果函数f(x)在开区间(a,b)内每一点处都可导,则称f(x)在(a,b)内可导.
(2) 如果f(x)在(a,b)内可导,且![]() 与
与![]() (b)均存在,则称f(x)在闭区间[a,b]上可导.
(b)均存在,则称f(x)在闭区间[a,b]上可导.
设函数f(x)在区间I内可导,则对I内的每一点x,都有一个确定的值f′(x)与之对应,由此构成了一个新的函数f′(x),称这个新函数为函数f(x)在集合I内的导函数(简称导数),记作f′(x)![]() 或y′.
或y′.
将式(2-1)中的x0换成x,便可得导函数的表达式:
![]()
(2-3)
必须指出,上式中Δx是求极限时的变量,x为求该极限时的常数.
由式(2-1)与(2-3)可知,函数f(x)在x0处的导数f′(x0)就是导函数f′(x)在x=x0处的函数值,即
![]()
特别指出的是[f(x0)]′=0,不能将f′(x0)与[f(x0)]′相混淆.
一般地,求函数y=f(x)的导数步骤为:
① 求函数的增量Δy=f(x+Δx)-f(x);
② 求增量比![]() ;
;
③ 求增量比的极限![]() .
.
若该极限![]() 存在,则函数y=f(x)在x处可导,且f′(x)
存在,则函数y=f(x)在x处可导,且f′(x)![]() ;若该极限不存在,则函数y=f(x)在x处不可导.
;若该极限不存在,则函数y=f(x)在x处不可导.
例6 求f(x)=C(C为常数)的导数.
解 ∀x∈R,由于
![]()
故
(C)′=0
(2-4)
例7 求幂函数y=xμ(μ为常数)的导数.
解 设y=xμ的定义域为D,∀x∈D,由于


故
(xμ)′=μxμ-1
(2-5)
特别地,
(xn)′=nxn-1 (n为整数)
式(2-5)称为幂函数的求导公式,利用其可直接求幂函数的导数,例如:

例8 求y=cosx的导数,并求![]() .
.
解 ∀x∈R,由
![]()
则

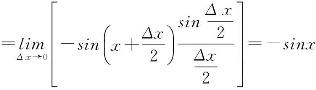
即
(cosx)′=-sinx
(2-6)
因此
![]()
同理可证:
(sinx)′=cosx
(2-7)
例9 求对数函数y=lnx的导数.
解 ∀x>0,由于
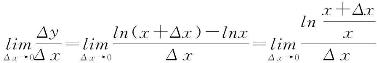

故
![]()
(2-8)
例10 求指数函数y=ax(a>0,a≠1)的导数.
解 ∀x∈R,由于
![]()
![]() =axlna
=axlna
故
(ax)′=axlna
(2-9)
特殊地,取a=e,有
(ex)′=ex
(2-10)
2.1.2 导数的几何意义
由导数的定义并结合平面曲线的切线问题可知,在几何上,可导函数f(x)的导数f′(x)等于曲线y=f(x)在点M(x,y)处的切线的斜率.
当函数f(x)在点x0处可导时,曲线y=f(x)在点M0(x0,f(x0))处有切线:
y-f(x0)=f′(x0)(x-x0)
当函数f(x)在点x0处连续且f′(x0)=∞时,曲线y=f(x)在x0处有一垂直于x轴的切线x=x0;当函数f(x)在点x0处连续但不可导且f′(x0)≠∞时,曲线y=f(x)在x0处没有切线.
如由例2可知,函数![]() 在x=0处连续但不可导,而
在x=0处连续但不可导,而
![]()
所以曲线![]() 在x=0处有一条垂直于x轴的切线(如图2-1所示)
在x=0处有一条垂直于x轴的切线(如图2-1所示)
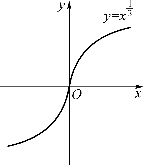
图2-1
x=0
例11 求曲线f(x)=x3在点(1,1)处的切线方程.
解 曲线在点(1,1)处的切线斜率为
k=f′(1)=3
所以切线方程为
y-1=3(x-1)
即
y=3x-2
2.1.3 函数的可导性与连续性之间的关系
由例4可知,函数f(x)=|x|在x=0处连续但不可导,因此当函数f(x)在x处连续时未必可导.但通过下面的证明可知,函数连续是可导的必要条件.
定理1 若函数y=f(x)在x处可导,则它在x处必连续.
证 因为函数y=f(x)在x处可导,所以
![]()
则
![]()
故f(x)在x处连续.
例12 设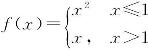 ,讨论f(x)在x=1处的连续性与可导性.
,讨论f(x)在x=1处的连续性与可导性.
解 由于
![]()
故
![]()
即f(x)在x=1处连续.又由于
![]()
![]()
即![]() (1),故f(x)在x=1处不可导.
(1),故f(x)在x=1处不可导.
由例12可知:若函数y=f(x)在x处连续,则它在x处未必可导,即定理1的逆定理不成立.
注意分段函数的不可导点往往出现在分段点处,讨论分段函数在其分段点处的可导性时,必须用左、右导数的定义,只有在左、右导数都存在且相等的条件下,函数在此分段点处才可导.
习题2.1
1.说明下列式子的含义:
(1) [f(x0)]′. (2) f′[φ(x0)].
2.设f(x)=2+4x2,用导数的定义求f′(1).
3.设f(x)=x(x+1)(x+2)…(x+n),用导数的定义求f′(0).
4.求曲线y=ex在点(0,1)处的切线方程.
5.在抛物线y=x2上取横坐标为x1=1及x2=3的两点,作过这两点的割线,问该抛物线上哪一点的切线平行于这条割线?
6.求曲线y=cosx(0<x<π)的垂直于直线![]() 的切线方程.
的切线方程.
7.设f(x)在x0处可导,试求极限![]() .
.
8.设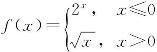 ,求f′(x).
,求f′(x).
9.设函数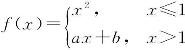 在x=1处可导,求a,b的值.
在x=1处可导,求a,b的值.
10.讨论函数 在x=0处的连续性与可导性.
在x=0处的连续性与可导性.
11.设f(x)在x=0处连续,且![]() ,证明f(x)在x=0处可导,并求f′(0).
,证明f(x)在x=0处可导,并求f′(0).
2.2 导数的运算法则与基本公式
上一节给出了导数概念,并利用导数的定义求出了部分基本初等函数的导数,然而对一般的函数,若依靠定义求导数是非常不方便甚至是困难的.导数的计算主要还是要利用导数的运算法则与基本公式,本节及下一节将讨论各类函数的求导法则和方法.下面先建立导数的运算法则,并在此基础上得到基本初等函数的求导公式.
2.2.1 求导的四则运算法则
求导法则Ⅰ 设函数u(x),v(x)在x处可导,则u(x)±v(x)及u(x)·v(x)也在x处可导,且
[u(x)±v(x)]′=u′(x)±v′(x)
(2-11)
[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x)
(2-12)
若再增加条件v(x)≠0,则函数![]() 在x处也可导,且
在x处也可导,且
![]()
(2-13)
证 令f(x)=u(x)±v(x),g(x)=u(x)·v(x),由导数定义与极限的运算法则,得
![]()
![]()
![]()
![]()
=u′(x)±v′(x)
![]()
=![]()
![]()
由于v(x)在x处可导必连续,则
![]()
再由极限运算法则与导数定义得
g′(x)=u′(x)v(x)+u(x)v′(x)
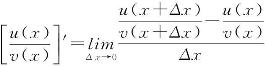
![]()
![]()
![]()
![]()
![]()
![]()
由此得两个函数的商的求导法则:
![]()
证毕.
利用常数函数的导数为零,再由求导法则Ⅰ中的式(2-12)可得如下推论.
推论1 设u(x)在x处可导,c为常数,则cu(x)在x处也可导,且
[cu(x)]′=cu′(x)
(2-14)
另外求导法则Ⅰ中的加法、减法与乘法的运算法则可推广到有限个可导函数的情形.
推论2 设u(x),v(x),w(x)均在x处可导,则u(x)+v(x)+w(x)与u(x)v(x)w(x)在x处也可导,且
[u(x)+v(x)+w(x)]′=u′(x)+v′(x)+w′(x)
(2-15)
[u(x)v(x)w(x)]′=u′(x)v(x)w(x)+u(x)v′(x)w(x)+u(x)v(x)w′(x)
(2-16)
例1 求对数函数y=logax的导数.
解 由于![]() ,则
,则
![]()
即
![]()
(2-17)
例2 求y=tanx的导数.
解 由商的求导法则,得
![]()
即
(tanx)′=sec2x
(2-18)
同理可得
(cotx)′=-csc2x
(2-19)
(secx)′=tanxsecx
(2-20)
(cscx)′=-cotxcscx
(2-21)
例3 求函数![]() 的导数.
的导数.
解 由导数加法与减法运算的法则,得
![]()
例4 求f(x)=extanx的导数.
解 由导数乘法运算的法则,得
f′(x)=(ex)′tanx+ex(tanx)′=extanx+exsec2x=ex(tanx+sec2x)
例5 求y=(x+1)(1-x)(3x+2)的导数.
解 由导数加法、减法与乘法运算的法则,得
y′ =(x+1)′(1-x)(3x+2)+(x+1)(1-x)′(3x+2)+(x+1)(1-x)(3x+2)′
=(1-x)(3x+2)-(x+1)(3x+2)+3(x+1)(1-x)
=-9x2-4x+3
例6 求![]() 的导数.
的导数.
解 y=cotx+1+2log3x-cosx,由导数加法与减法运算的法则,得
![]() +sinx
+sinx
例7 求![]() 的导数.
的导数.
解 由商的求导法则,得
![]()
2.2.2 反函数与复合函数的求导法则
1) 反函数的求导法则
求导法则Ⅱ 设y=f(x)在区间Ix内单调、可导,且f′(x)≠0,则其函数x=φ(y)在相应的区间Iy内也单调、可导,且![]() .
.
证 设函数的y=f(x)的反函数x=φ(y)的自变量y的增量为Δy,则相应地x的增量为Δx.由函数可导必连续的性质及反函数的连续性可得,x=φ(y)在区间Iy内单调、连续,因此当Δy→0时,有Δx→0.且当Δy≠0时,有Δx≠0,则∀y,y+Δy∈Iy,设Δy≠0,有
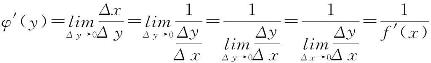
证毕.
例8 求反正弦函数y=arcsinx(|x|<1)的导数.
解 由于x=siny在区间![]() 内单调、可导,且其导数cosy≠0.因此,其反函数y=arcsinx在相应的区间(-1,1)内单调、可导,且由反函数求导公式得
内单调、可导,且其导数cosy≠0.因此,其反函数y=arcsinx在相应的区间(-1,1)内单调、可导,且由反函数求导公式得
![]()
即
![]()
(2-22)
同理可得
![]()
(2-23)
![]()
(2-24)
![]()
(2-25)
2) 复合函数的求导法则
很多情况下还会遇到复合函数的求导问题,下面推导复合函数的求导公式.
求导法则Ⅲ 设函数u=φ(x)在x处可导,函数y=f(u)在相应的点u处可导,则复合函数y=f[φ(x)]在x处也可导,且
(f[φ(x)])′=f′(u)φ′(x)
(2-26)
或
![]()
(2-26′)
证 设x有增量Δx,则相应地u有增量Δu,复合函数y有增量Δy.
由u=φ(x)在x处可导则必连续可知,当Δx→0时,有Δu→0.
当Δu≠0时,则
![]()
![]()
当Δu=0时,则相应地Δy=0,则必有![]() 及
及![]() ,故
,故![]() 也成立.
也成立.
因此复合函数y=f[φ(x)]在x处的求导法则为
(f[φ(x)])′=f′[φ(x)]·φ′(x)
上式中(f[φ(x)])′表示复合后的函数y=f[φ(x)]对自变量x的导数,f′[φ(x)]表示函数f(u)对u的导数.
该求导法则可以推广到有限个函数复合的情形.
推论3 设函数y=f(u),u=φ(v),v=ψ(x)复合成函数y=f{φ[ψ(x)]},若f(u),φ(v),ψ(x)均可导,则复合函数f{φ[ψ(x)]}也可导,且有
(f{φ[ψ(x)]})′=f′(u)·φ′(v)·ψ′(x)
(2-27)
或
![]()
(2-27′)
上式右端的求导法则,按y→u→v→x的顺序,就像一条链子一样,因此通常将复合函数的求导法则Ⅲ及推论3称为链式法则.
例9 求函数y=ln|x|的导数.
解
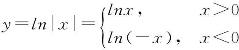
当x>0时,![]() ;
;
当x<0时,y′=[ln(-x)![]() .
.
因此
![]()
(2-28)
上式也是一个常用的公式,必须熟记.
2.2.3 求导的基本公式
利用导数定义及求导法则Ⅰ、Ⅱ,已经得到了所有基本初等函数的导数公式,习惯上称之为求导基本公式(简称求导公式),归纳如下:
(1) (c)′=0.
(2) (xμ)′=μxμ-1.
(3) (ax)′=axlna.特别地,(ex)′=ex.
![]() .特别地,
.特别地,![]() 及
及![]() .
.
(5) (sinx)′=cosx.
(6) (cosx)′=-sinx.
(7) (tanx)′=sec2x.
(8) (cotx)′=-csc2x.
(9) (secx)′=secxtanx.
(10) (cscx)′=-cscxcotx.
![]() <1).
<1).
![]() <1).
<1).
![]() .
.
![]() .
.
2.2.4 初等函数的导数
由于初等函数是由基本初等函数经过有限次四则运算及有限次函数复合而构成的用一个解析式表示的函数,因此结合前面的求导法则与求导公式可推得:初等函数在其定义区间上处处可导,其导函数只要按照函数的结构,利用相应的求导公式或法则就可求出.
例10 求下列函数的导数:
(1) y=te2t. ![]() .
.
解 (1) y′=e2t+t·2e2t=(1+2t)e2t.
(2) 由于
![]()
故
![]()
例11 设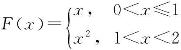 ,求F′(x).
,求F′(x).
解 当x≠1时,F(x)在相应的定义区间上都是初等函数,故利用求导公式可得
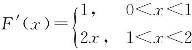
由于x=1是函数f(x)的分界点,且f(x)在x=1的两侧的表达式不同,所以要利用该点的左、右导数的定义,求得
![]()
![]()
故F′(1)不存在.
综上

例12 设f(x)为可导函数,求函数y=f2(sinx)的导数.
解 由复合函数的求导法则可得
y′ =2f(sinx)[f(sinx)]′=2f(sinx)f′(sinx)sin′x
=2f(sinx)f′(sinx)cosx=2cosxf(sinx)f′(sinx)
例13 设函数 在点x=0处连续且可导,求a,b的值.
在点x=0处连续且可导,求a,b的值.
解 由于x=0是函数f(x)的分界点,且f(x)在x=0的两侧的表达式不同,所以要利用定义求该点的左、右极限与导数,再考察其连续性与可导性,先考虑f(x)在x=0处的连续性,由
![]()
得
1=b
再考虑f(x)在x=0处的可导性,由
![]()
![]()
得
0=a
解得a=0,b=1.
习题2.2
1.填空.
(1) (________)![]() (________)
(________)![]() .
.
(3) (________)′=xsinx2. (4) (________)′=e2x.
2.求下列函数的导数:
(1) y=3x2-2cosx+3. ![]() .
.
(3) y=5x3-2x+3e. (4) y=2tanx-sinπ+cscx.
(5) y=x2lnx. ![]() .
.
![]() -2arctanx. (8) y=(2x+5)3.
-2arctanx. (8) y=(2x+5)3.
(9) y=e-3x2. (10) y=4sinx.
![]() ).
). ![]() .
.
(13) y=ln|x3-x2|. ![]() .
.
3.求下列函数在指定点处的导数:
(1) y=(x2+x+1)100,x=-1. ![]() .
.
4.求下列函数的导数(其中f(x)为可导函数):
(1) y=f2(ex). (2) y=f(x2).
5.设函数φ(t)=f(x0+at),又f′(x0)=a,求φ′(0).
6.已知曲线y=ax4+bx3+cx2+d与直线y=11x-5在点(1,6)处相切,并经过点(-1,8),且在点(0,3)处有一水平切线.求a,b,c,d的值.
7.设f(x)=5|2-x|,求f′(x).
8.设函数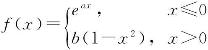 处处可导,求a,b的值.
处处可导,求a,b的值.
9.已知![]() ,求f′(x).
,求f′(x).
2.3 高阶导数
1) 高阶导数的定义
我们知道运动学中变速直线运动中的速度函数v(t)是路程函数s(t)对时间t的导数s′(t),而加速度a(t)是速度函数v(t)对时间t的导数,即
a(t)=v′(t)=[s′(t)]′
因此加速度a(t)是路程函数s(t)对t的导数的导数,称为函数s(t)对t的二阶导数.
一般地,函数y=f(x)的导数仍是x的函数,如果导函数y′=f′(x)的导数存在,则称此导函数f′(x)的导数为函数y=f(x)的二阶导数,记作![]() 或
或![]() .
.
由导数定义可知
![]()
(2-29)
依次类推,如果f″(x)的导数存在,就称这个二阶导数的导数为函数y=f(x)的三阶导数,记作y‴,f‴(x)或![]() .
.
一般地,如果函数y=f(x)的(n-1)阶导数的导数存在,就称这个导数为函数y=f(x)的n阶导数,记作y(n),f(n)(x)或![]() .
.
由导数定义可知
![]()
(2-30)
二阶及二阶以上的导数统称为高阶导数.
当x=x0时,对应的n阶导函数的值记作![]() 或
或![]() .
.
显然,求高阶导数就是对一个函数进行连续多次的求导运算,再运用归纳法就可得出一些常见函数的高阶导数.
例1 求n次多项式函数y=a0+a1x+a2x2+…+anxn的各阶导数.
解
y′=a1+2a2x+…+nanxn-1
y″=2a2+6a3x+…+n(n-1)anxn-2
…
每求导一次,多项式的次数就降一次,对原来的多项式进行连续n次求导运算后,可得
y(n)=n!an
显然y(n)是一个常数,因此
y(n+1)=y(n+2)=…=0
即n次多项式的一切高过n阶的导数都等于零.
例2 求y=abx的n阶导数.
解
y′=abxblna
y″=abxblna·blna=abx(blna)2
…
y(n)=abx(blna)n
即
(abx)(n)=abx(blna)n
(2-31)
特别地,在式(2-31)中取b=1,有
(ax)(n)=ax(lna)n
(2-32)
在式(2-31)中取a=e,有
(ebx)(n)=bnebx
(2-33)
再在上式中取b=1,有
(ex)(n)=ex.
(2-34)
例3 求y=(1+x)μ(μ∈R)的n阶导数.
解 (1) 当μ∉N+,则
y′=μ(1+x)μ-1
y″=μ(μ-1)(1+x)μ-2
…
y(n)=μ(μ-1)…(μ-n+1)(1+x)μ-n
(2) 当μ∈N+,则
当n<μ时,
y(n)=μ(μ-1)…(μ-n+1)(1+x)μ-n
当n=μ时,
y(n)=n!
当n>μ时,
y(n)=0
特别地,当μ=-1时,有
![]()
(2-35)
例4 求y=ln(1+x)的n阶导数.
解![]() ,再由例3中的式(2-35),可得
,再由例3中的式(2-35),可得
![]()
(2-36)
例5 求y=sinax的n阶导数.
解
![]()
![]()
y‴![]()
…
一般地
![]()
(2-37)
类似可得
![]()
(2-38)
利用上述例题中的结论及求高阶导数的方法可求一些简单函数的高阶导数.
例6 设y=e2x,求y(n).
解 利用上面式(2-33)的结果可得:
y(n)=(e2x)(n)=2ne2x
例7 设f(x)=cos2x,求f(n)(0).
解 由f′(x)=-2sinxcosx=-sin2x,则再对f′(x)求n-1阶导数,得
![]()
将x=0代入上式,得
![]()
一般函数的高阶导数的表达式是相当繁琐的,为了便于计算高阶导数,下面介绍两个常用的高阶导数的运算法则.
2) 高阶导数的运算法则
(1) 高阶导数的加、减运算法则
设u(x)与v(x)都在x处具有n阶导数,则
[u(x)±v(x)]′=u′(x)±v′(x)
[u(x)±v(x)]″=[u′(x)±v′(x)]′=u″(x)±v″(x)
…
利用数学归纳法,可得
[u(x)±v(x)](n)=u(n)(x)±v(n)(x)
(2-39)
此结论可推广到有限个函数的代数和的情形.
例8 设![]() ,求y(n).
,求y(n).
解
![]()
利用式(2-35)的结论以及高阶导数的加法与减法运算法则,得
![]()
![]()
(2) 高阶导数的乘法运算法则
设u(x)与v(x)都在x处具有n阶导数,则
[u(x)v(x)]′=u′(x)v(x)+u(x)v′(x)
[u(x)v(x)]″ =[u′(x)v(x)]′+[u(x)v′(x)]′
=u″(x)v(x)+u′(x)v′(x)+u′(x)v′(x)+u(x)v″(x)
=u″(x)v(x)+2u′(x)v′(x)+u(x)v″(x),
[u(x)·v(x)]‴ =[u″(x)v(x)]′+2[u′(x)v′(x)]′+[u(x)v″(x)]′
=u‴(x)v(x)+u″(x)v′(x)+2u″(x)v′(x)
+2u′(x)v″(x)+u′(x)v″(x)+u(x)v‴(x)
=u‴(x)v(x)+3u″(x)v′(x)+3u′(x)v″(x)+u(x)v‴(x)
…
用数学归纳法可以证明
![]()
![]()
![]()
(2-40)
上式是两个函数乘积的n阶导数公式,也称为莱布尼兹(Leibniz)公式.由于其结果中的系数与代数中二项式定理中相应的系数一致,因此常借助二项式定理的系数与项的规律来帮助记忆莱布尼兹公式.
例9 设f(x)=(x3+2)ex,求f(20)(x)及f(20)(0).
解 令u=ex,v=x3+2,则
u(k)=ex (k=1,2,…,20)
v′=3x2, v″=6x, v‴=6, v(k)=0 (k=4,5,…,20)
代入莱布尼兹公式即式(2-40),得
f(20)(x) =[(x3+2)ex](20)
![]()
![]() ‴(ex)(17)
‴(ex)(17)
=ex(x3+60x2+1 140x+6 842)
故
![]()
习题2.3
1.求下列函数的二阶导数:
(1) y=43x-1. (2) y=2x2+lnx.
![]() ). (4) y=xex2.
). (4) y=xex2.
2.设f(x)具有二阶导数,求下列函数y的二阶导数![]() :
:
(1) y=ln[f(x)]. (2) y=f(x2).
3.验证函数y=c1ex+c2e-x(c1,c2为常数)满足关系式y″-y=0.
4.求下列函数的n阶导数:

2.4 隐函数与参数方程确定的函数的导数
以前我们提到的函数都可以表示成y=f(x)的形式,其中函数f(x)是由x的解析式表示出,称为显函数.除了显函数之外,隐函数、参数方程等也是函数的重要表现形式.隐函数未必能显化,参数方程也未必能消去参数成为显函数.因此它们的导数仅用前面介绍的求导法则与公式未必能求出.下面着重讨论隐函数、参数方程确定的函数的求导方法.
2.4.1 隐函数的导数
1) 隐函数求导法
(1) 隐函数的导数
一般地,如果方程F(x,y)=0在一定条件下,当x在某区间内任取一值时,相应地总有满足这个方程的唯一的y值存在,那么,就称方程F(x,y)=0在该区间上确定了一个隐函数y=y(x).
把一个隐函数化为显函数,称为隐函数的显化.例如方程x2+2y=1确定的函数可显化为![]() (1-x2).但有些隐函数的显化是困难的,甚至是不可能的.而在实际问题中,往往需要计算隐函数的导数,那么能否对隐函数不显化,而直接从方程F(x,y)=0计算该隐函数的导数
(1-x2).但有些隐函数的显化是困难的,甚至是不可能的.而在实际问题中,往往需要计算隐函数的导数,那么能否对隐函数不显化,而直接从方程F(x,y)=0计算该隐函数的导数![]() 呢?下面给出解决这个问题的方法.
呢?下面给出解决这个问题的方法.
设方程F(x,y)=0确定了可导函数y=y(x),因此把它代回原方程中就得到恒等式:
F[x,y(x)]=0
对上述恒等式的两端求x的导数,所得的结果也必然相等,但应注意,方程的左端F[x,y(x)]是将y=y(x)代入方程F(x,y)中的结果,所以求导时其中的y要看作x的函数,然后用复合函数的求导法去求导,这样就可得到一个含有欲求的导数![]() 的等式,从中可解出
的等式,从中可解出![]() .这就是所谓的隐函数求导法.
.这就是所谓的隐函数求导法.
例1 设方程exy+y2=cosx确定y为x的函数,求![]() .
.
解 对方程两边求x的导数,得
![]() =-sinx
=-sinx
解得
![]()
例2 求曲线xy+ey=1在点(0,0)处的切线方程.
解 方程两边分别对x求导,得
y+xy′+ey·y′=0
将x=0,y=0代入上式,得
![]()
则曲线在(0,0)点处的切线方程是
y=0
(2) 隐函数的二阶导数
如果需要求隐函数的二阶导数,只要对含有隐函数的一阶导数![]() 的方程两边再求自变量的导数,便可得到一个含有隐函数的二阶导数
的方程两边再求自变量的导数,便可得到一个含有隐函数的二阶导数![]() 的等式,再将一阶导数
的等式,再将一阶导数![]() 的表达式代入该方程,就可从中解出
的表达式代入该方程,就可从中解出![]() .这就是隐函数的二阶导数的求法.
.这就是隐函数的二阶导数的求法.
例3 设函数y=y(x)是由方程ex-ey-xy=0确定的隐函数,求![]() .
.
解 当x=0时,代入原方程即可求得y=0,在方程两边对x求导,得
![]()
(2-41)
再对上式求x的导数,得
![]()
(2-42)
将x=0,y=0代入式(2-41),解得![]() ,再将
,再将![]() 代入式(2-42),解得
代入式(2-42),解得
![]()
2) 对数求导法
利用隐函数求导法还可以方便地求出由几个因子通过乘、除、乘方、开方所构成的比较复杂的函数(包括幂指函数y=[f(x)]g(x))的导数,具体做法如下:对函数两边先取对数,化乘除为加减,化乘方、开方为乘积,得到包含原来函数的方程,再按隐函数的求导方法求导即可,称这种求导法为对数求导法.
例4 设y=xx(x>0),求![]() .
.
解 在等式两边取对数,得
lny=xlnx
对上式两边对x求导,得
![]()
解得
![]() =xx(lnx+1)
=xx(lnx+1)
对数求导法不仅可以用来求幂指函数的导数,从下面的例子可以看到,此方法对求某些仅含有乘、除、乘方、开方运算的函数导数也同样适用.
例5 求![]() 的导数.
的导数.
解 在已知函数两边取对数,得
![]()
上式两边对x求导,得
![]()
解得
![]()
2.4.2 参数方程确定的函数的导数
1) 参数方程确定的函数的导数
有时函数由参数方程 来表示更方便且简单,如
来表示更方便且简单,如 (0≤t≤π)表示以R为半径、原点为圆心的上半圆周曲线
(0≤t≤π)表示以R为半径、原点为圆心的上半圆周曲线![]() .星形线的直角坐标方程为
.星形线的直角坐标方程为![]() ,其参数方程为
,其参数方程为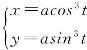 (0≤t≤2π),显然星形线的参数方程更为简单.
(0≤t≤2π),显然星形线的参数方程更为简单.
一般地,设参数方程 ,若t∈(α,β)时,x=x(t),y=y(t)都有连续的导数,且x′(t)≠0,可以证明x=x(t)必有单值反函数t=t(x),代入y=y(t)中,得y=y[t(x)],因此在所给条件下,参数方程
,若t∈(α,β)时,x=x(t),y=y(t)都有连续的导数,且x′(t)≠0,可以证明x=x(t)必有单值反函数t=t(x),代入y=y(t)中,得y=y[t(x)],因此在所给条件下,参数方程 (α,β))确定了y是x的函数y=y[t(x)],它必定可导,由复合函数与反函数的求导法则,求得其导数为
(α,β))确定了y是x的函数y=y[t(x)],它必定可导,由复合函数与反函数的求导法则,求得其导数为

(2-43)
称上式为参数方程确定的函数的导数公式.
例6 求摆线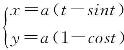 在
在![]() 时的切线方程.
时的切线方程.
解 将![]() 代入参数方程中,得
代入参数方程中,得![]() a.又
a.又
![]()
则![]() =1,因此摆线在
=1,因此摆线在![]() 时的切线方程为
时的切线方程为
![]()
即
![]()
2) 参数方程确定的函数的二阶导数
显然参数方程 的导函数
的导函数![]() 仍是参数t的函数,因此其导函数
仍是参数t的函数,因此其导函数![]() 仍然可用参数方程表示:
仍然可用参数方程表示:

设x=x(t),y=y(t)都有连续的二阶导数,且x′(t)≠0,则利用参数方程的求导公式可得参数方程确定的函数的二阶导数为:

![]()
(2-44)
必须指出式(2-44)虽然可以作为参数方程 确定的函数的二阶导数公式,但使用它并不方便,而用参数方程的求导方法求二阶导数如下:
确定的函数的二阶导数公式,但使用它并不方便,而用参数方程的求导方法求二阶导数如下:

该方法不仅更为方便,还可以用它求该参数方程确定的函数的更高阶的导数.
例7 设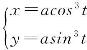 ,求
,求![]() .
.
解
![]()
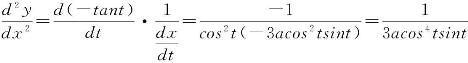
*2.4.3 相关变化率
在许多实际问题中经常会遇到这样一类问题:在某一变化过程中,变量x与y都是变量t的函数,而x与y之间又存在某种依赖关系,若x=x(t),y=y(t)都可导,则变化率![]() 之间也存在某种依赖关系,这两个相互依赖的变化率称为相关变化率.
之间也存在某种依赖关系,这两个相互依赖的变化率称为相关变化率.
若已知x与y的函数关系及其中某一个变量对t的变化率,就可以求出另一个变量对t的变化率.具体方法为:根据问题的实际情况建立x与y的关系等式,对该关系等式求t的导数,得到两个相关变化率![]() 与
与![]() 之间的方程,再利用其中已知的变化率求出另一个变化率.
之间的方程,再利用其中已知的变化率求出另一个变化率.
例8 设有一个球体,其半径以0.01 m/s的速度增加,当其半径达到2 m时,求体积及表面积的增加速率.
解 设球的半径为R,则体积为
![]()
表面积为
S=4πR2
分别对上面两式的两边求时间t的导数,得
![]()
将R′(t0)=0.01 m/s,R(t0)=2 m代入上面两式中,得
![]()
![]()
故球体的体积增加速率为0.16π(m3/s),表面积增加速率为0.16π(m2/s).
习题2.4
1.求下列方程所确定的隐函数y=y(x)的导数y′或在指定点处的导数:
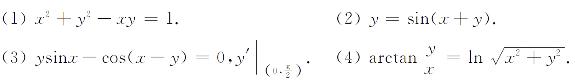
2.用对数求导法求下列函数的导数:

3.求下列参数方程所确定的函数的导数![]() 或在指定点处的导数:
或在指定点处的导数:

4.设由方程y=1+xey确定函数y=y(x),求![]() .
.
5.设由方程ey-e-x+xy=0确定函数y=y(x),求y′(0)及y″(0).
6.求由下列参数方程所确定的函数的二阶导数![]() :
:
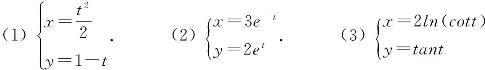 .
.
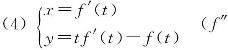 (t)存在且不为零).
(t)存在且不为零).
7.求曲线![]() 在
在![]() 的对应点处的切线方程与法线方程.
的对应点处的切线方程与法线方程.
8.在曲线x2+2xy+y2-4x-5y+3=0上求一点,使曲线在该点的切线与直线2x+3y=0平行,并求出该切线的方程.
9.已知曲线 在t=1时过原点,且曲线在原点的切线平行于直线2x-y+1=0,求a,b,c的值.
在t=1时过原点,且曲线在原点的切线平行于直线2x-y+1=0,求a,b,c的值.
10.若曲线y=f(x)与y=sinx在原点相切(有公共的切线),求![]() .
.
*11.一气球以40 cm3/s的速度充气,当球半径为10 cm时,求球半径的增长率.
2.5 函数的微分及其应用
某些实际问题中,有时需要讨论自变量发生微小改变时所产生的函数增量的计算问题.微分提供了函数增量的一种简便而有效的近似算法,为我们研究函数在一点处的形态提供了重要工具,因而微分也是微分学中重要的基本概念之一.
2.5.1 微分的概念
先考察一个实例.
例1 有一块正方形金属薄片,因环境温度发生了微小的的变化,其边长从x0变为x0+Δx,问薄片的面积将改变多少?
解 设金属薄片的边长为x,则其面积A=x2,当边长在x0处改变了Δx时,对应面积的改变量为
![]()

图2-2
从上式可看出,ΔA由两部分组成,一部分是Δx的线性函数2x0Δx,即图2-2中带有斜阴影线的两个矩形面积之和;另一个是(Δx)2,即图2-2中带有交叉斜线的小正方形的面积.当|Δx|很小时,2x0Δx是ΔA的主要部分,而当Δx→0时,(Δx)2是比Δx高阶的无穷小.可见,用2x0Δx作为ΔA的近似值时,其误差达到(Δx)2,它是o(Δx),因此
ΔA≈2x0Δx
为了方便,数学上把这个近似代替函数改变量ΔA的线性部分2x0Δx称为该函数的微分.由此给出如下函数微分的定义.
定义1 设y=f(x)在x0的某邻域U(x0)内有定义,Δx为自变量x的增量,且x0+Δx∈U(x0),若相应函数的增量Δy=f(x0+Δx)-f(x0)可表示为
Δy=A(x0)Δx+ο(Δx)
(2-45)
其中A(x0)是与Δx无关的常量,则称函数y=f(x)在点x0可微,其中的关于Δx的线性部分A(x0)Δx称为函数y=f(x)在x0处的微分,记作![]() .即
.即
![]()
下面利用函数在点x0处可微及可导的定义推出函数可微的等价条件以及微分公式.
定理1 函数y=f(x)在x0处可微的充要条件是y=f(x)在x0处可导,且
![]()
证 (1) 先证充分性.
设函数y=f(x)在点x0处可导,即
![]()
则
![]() (其中
(其中![]()
由此
Δy=f(x0+Δx)-f(x0)=f′(x0)Δx+Δx·α(Δx)
上式中f′(x0)是与Δx无关的一个量,且Δx·α(Δx)=o(Δx),故y=f(x)在点x0处可微,且
![]()
(2) 再证必要性.
设函数y=f(x)在点x0处可微,则存在与Δx无关的量A,使
Δy=AΔx+ο(Δx)
故
![]()
则有
![]()
即y=f(x)在点x0处可导,且f′(x0)=A.因而有
![]()
证毕.
对于函数y=x,由于y′=1,则其微分为dx=Δx,因此常把dx称为自变量x的微分,因此函数y=f(x)的微分公式常写为
dy=f′(x)dx
(2-46)
例如,函数y=sinx的微分为
dy=cosxdx
需要指出,在微分公式(2-46)中,dy,f′(x),dx是三个具有独立意义的量,因此由微分公式(2-46)可得
![]()
上式将导数f′(x)看作微分dy与dx的商,所以导数也称为微商.
应当注意,微分与导数虽然有等价关系,却是有区别的:导数是函数在一点处的变化率,而微分是函数在一点处的自变量的增量所引起的函数的改变量的近似值;另外导数的值只与x有关,而微分的值与x和Δx都有关.
设y=f(x)在x的集合I内每一点都可导,我们结合导数的基本公式,再利用微分与导数的关系式(2-46),就可得到求微分的基本公式.为了便于对照,表2-1中列出了基本初等函数的导数与微分公式.
表2-1 基本初等函数的导数与微分公式
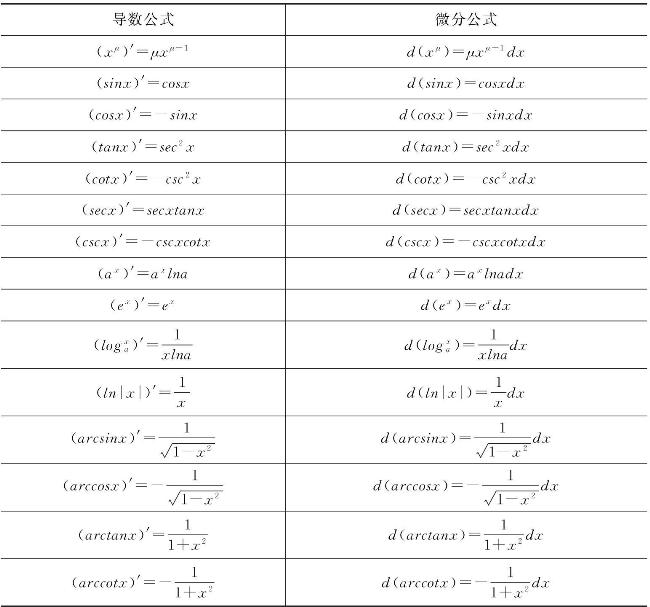
由定理1及公式(2-46)可知求微分的步骤为:先求函数的导数f′(x),再写出其微分为
dy=f′(x)dx
例2 求y=x3,当x=4,Δx=0.01时的微分.
解 由于y′=3x2,故
dy=3x2·Δx
将x=4,Δx=0.01代入上式得
![]()
例3 求函数![]() 的微分.
的微分.
解 由于![]() ,故
,故
![]() dx
dx
2.5.2 微分的几何意义

图2-3
在曲线y=f(x)上取相邻两点M0(x0,y0),N(x0+Δx,y0+Δy),过M0作曲线的切线M0T,设切线M0T的倾角为α(图2-3),则在M0(x0,y0)处有
tanα=f′(x0)
M0Q=Δx
QN=Δy
因此
QP=M0Q·tanα=Δx·tanα=f′(x0)Δx
即
dy=QP
从图2-3中可知,Δy是曲线上纵坐标的增量,dy是切线上纵坐标的增量,可见微分的几何意义是:微分dy表示曲线y=f(x)在点M0处的切线上当x有增量Δx时,切线纵坐标的增量.
由微分的意义Δy≈dy可知,对于可微函数y=f(x),当|Δx|很小时,用微分表示函数增量的绝对误差|Δy-dy|也很小.因此,微分的意义在于在M0点邻近,可用切线段来近似代替曲线段,即局部线性化.因此微分的思想简单地说就是“以直代曲”.
2.5.3 微分的运算法则
由函数的和、差、积、商的求导法则,结合公式(2-46)可推得相应的微分运算法则,为了便于对照,列于表2-2中.
表2-2 函数的求导法则与微分法则
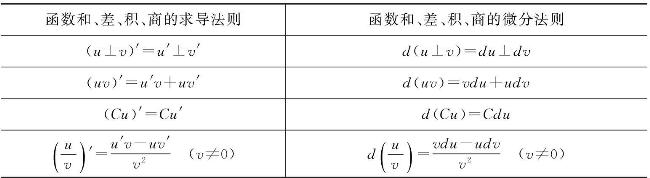
下面仅以乘积的微分法则为例加以证明.
由函数微分公式(2-46),有
d(uv)=(uv)′dx=(u′v+uv′)dx=u′dx·v+u·v′dx=vdu+udv
因此
d(uv)=vdu+udv
其他法则均可类似证明.请读者自证.
下面讨论复合函数的微分.
设函数y=f(u)可微,则dy=f′(u)du.
若上式中u是中间变量,函数u=φ(x)可微,则复合函数y=f[φ(x)]也可微,其微分
dy=(f[φ(x)])′dx=f′[φ(x)]·φ′(x)·dx=f′(u)du
可见,当u是中间变量时,dy也可表达为f′(u)du,与u是自变量时,在形式上是相同的.这个性质称为微分形式的不变性.它在微分的运算中很有用:在计算复合函数的微分时,可以把复合函数f[φ(x)]中的φ(x)当作一个整体变量直接对它求导,然后再求出φ(x)的微分即可.例如
d(sin2x)=(cos2x)d(2x)=2cos2xdx
例4 求![]() 的微分.
的微分.
解 解法
![]()
解法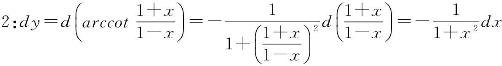
例5 求y=x2lnx的微分.
解 解法![]()
解法![]()
2.5.4 微分在近似计算中的应用
设y=f(x)在x0处可微,当f′(x0)≠0,且|Δx|很小时,则Δy≈dy,即
Δy=f(x0+Δx)-f(x0)≈f′(x0)Δx
(2-47)
记作x=x0+Δx,则
f(x)≈f(x0)+f′(x0)Δx
(2-48)
在工程技术中,经常利用上面两个微分近似公式来计算由于自变量发生微小变化而引起变化的函数的改变量与函数值相应的近似值.
例6 求当x由45°变到45°20′时,函数y=secx的增量的近似值.
解 利用微分近似公式(2-47)计算
Δy≈dy=secxtanxΔx
将![]() 代入上式,得
代入上式,得
![]()
例7 求![]() 的近似值.
的近似值.
解 利用近似公式(2-48)计算,取
![]()
则
![]()
故
![]()
特殊地,在公式f(x0+Δx)≈f(x0)+f′(x0)Δx中取x0=0,Δx=x有
f(x)≈f(0)+f′(0)x
(2-49)
将式(2-49)用到许多常用函数上,可得到一系列常用的近似公式,例如,当|x|较小时有
![]()
sinx≈x, tanx≈x
等等,请读者自证.
习题2.5
1.计算下列函数的微分:
(1) y=xlnx-x2. (2) y=tan2(1+2x2).
(3) y=e-axsinbx. (4) y=ln2(1-x).
(5) 由方程xsiny+y2ex=0确定的隐函数y=y(x).
(6) 由参数方程 (a为常数)确定的函数y=y(x).
(a为常数)确定的函数y=y(x).
2.设函数y=x3,计算在x=2处,Δx分别等于-0.1、0.01时的增量Δy及微分dy.
3.填空.
(1) d( )=2dx. (2) d( )=cosxdx.
(3) d( )=sec23xdx. (4) d( )=e-2xdx.
4.在半径为3 m的球体表面镀一层银,若镀层的厚度为0.1 cm,问大约需要多少银(用体积表示)?
5.利用f(x0+Δx)≈f(x0)+f′(x0)Δx,推导出下列近似公式:
(1) 当|x|很小时,sinx≈x.
(2) 当|x|很小时,ex≈1+x.
6.利用微分计算下列数值的近似值:
(1) arctan1.02.(2) e1.01.
总复习题2
1.填空与选择.
(1) 若f(x)为可导的偶函数,且f′(x0)=a,则f′(-x0)=________.
(2) 若f(x)![]() ,则f′(x)=________.
,则f′(x)=________.
(3) 设f(x)可导,则![]()
( )
(A) 0 (B) [f′(x)]2 (C) 2f′(x) (D) 2f(x)f′(x).
(4) 设f(x)可导,y=f(sinx),则dy=
( )
(A) f′(sinx)dsinx (B) f′(sinx)dx
(C) [f(sinx)]′dsinx (D) 以上都不对
(5) 下列函数中在点x=0处可导的是
( )
![]()
2.求下列函数的导数:
(1) y=sinx·lnx2. ![]() .
.
3.求方程xy-2x+2y=0确定的隐函数的导数![]() .
.
4.试求曲线x2+xy+2y2-28=0在点(2,3)处的切线与法线方程.
5.求下列函数的一阶、二阶导数:
(1) 设x3-siny-x2ey=0,求y″(0,0).
(2) 设 ,求
,求![]() .
.
6.已知f′(ex)=x(x>0),求f″(x).
7.设 ,试问:k取何值时,f″(0)存在?
,试问:k取何值时,f″(0)存在?
8.求下列函数的n(n≥2)阶导数:
![]() x.
x.
*9.向深8 cm、上顶直径为8 cm的空正圆锥体容器中注水,其速率为4 cm3/min,当水深为5 cm时,问水面上升的速率为多少?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















