以上例子说明:有些方程组有唯一解,有些方程组有无穷解,有些方程组无解.究竟方程组满足什么条件时有唯一解、无穷解或者无解是我们将要研究的问题.下面先给出线性方程组的一般形式,再讨论其有解的条件.
设含有n个未知量,m个方程的线性方程组为
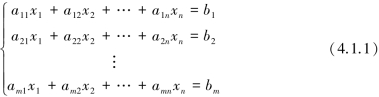
记矩阵

则线性方程组4.1.1写成矩阵形式
AX=b (4.1.2)
又记矩阵
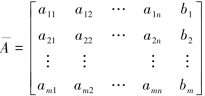
A和A分别称为线性方程组4.1.1的系数矩阵和增广矩阵.
若记列向量
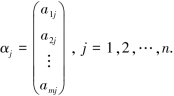
则由向量的线性表示,线性方程组4.1.1又可写成向量形式
x1α1+x2α2+…+xnαn=b (4.1.3)
式4.1.1,4.1.2,4.1.3是同一线性方程组的不同表现形式,在研究线性方程组时,根据需要选择不同的形式.
当常数项b1,b2,…,bm不全为0时,称AX=b为非齐次线性方程组;当常数项b1,b2,…,bm全为0时,称AX=b为齐次线性方程组.
如果线性方程组4.1.1中的x1,x2,…,xn分别用数c1,c2,…,cn代替后可使
每个方程变成恒等式,则称有序数组c1,c2,…,cn构成的列向量

设有两个线性方程组Ⅰ和Ⅱ,如果方程组Ⅰ的每一个解都是方程组Ⅱ的解,并且方程组Ⅱ的每一个解都是Ⅰ的解,则称线性方程组Ⅰ和Ⅱ同解.
定理4.1.1 线性方程组4.1.1有解的充分必要条件是其系数矩阵与其增广矩阵具有相同的秩,即:R(A)=R(A).
证 (必要性)若线性方程组4.1.1有解,则由线性方程组的向量形式即式4.1.3知向量b可由向量组a1,a2,…,an表示.
由定义3.4.1(向量组等价的定义)知:向量组α1,α2,…,αn与向量组α1,α2,…,αn,b等价,进而由推论3.4.2可得R(α1,α2,…,αn)=R(α1,α2,…,αn,b),即R(A)=R(A).
(充分性)若R(A)=R(A),不妨设R(A)=R(A)=r,令αj1,αj2,…,αjr为α1,α2,…,αn的最大无关组,则αj1,αj2,…,αjr也为α1,α2,…,αn,b的最大无关组,所以b向量可由αj1,αj2,…,αjr线性表示,即b亦可由α1,α2,…,αn线性表示.
因此,线性方程组4.1.1有解.
证毕.
由定理4.1.1并结合向量的相关知识得到如下判定线性方程组4.1.1解的情况的结论:
推论4.1.1 对于线性方程组4.1.1:
(1)无解的充分必要条件是R(A)≠R(A);
(2)有唯一解的充分必要条件是R(A)=R(A)=n;
(3)有无穷多解的充分必要条件是R(A)=R(A)<n.
特别地,对于齐次线性方程组AX=O,显然X=O为其解向量(称之为零解),故齐次线性方程组总是有解的.那么,齐次线性方程组在什么条件下有非零解或只有零解呢?由定理4.1.1可知:
(1)R(A)=n⇔AX=O有唯一解(只有零解);
(2)R(A)<n⇔AX=O有无穷多解(有非零解).
当齐次线性方程组的系数矩阵A为n阶方阵时:
(1)R(A)=n,即|A|≠0时,AX=O只有零解;
(2)R(A)=r<n,即|A|=0时,AX=O有非零解.
例4.1.1 解齐次线性方程组
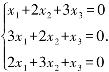
解 对齐次线性方程组的系数矩阵A施行初等行变换:
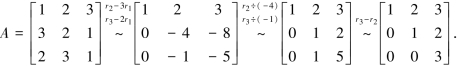
可见,R(A)=3=未知量的个数,因此该齐次线性方程组只有零解.
本例也可以计算该方程组的系数行列式,根据系数行列式的值不等于零,得到该方程组只有零解的结论.
例4.1.2 解非齐次线性方程组
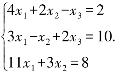
解 对方程组的增广矩阵A施行初等行变换:
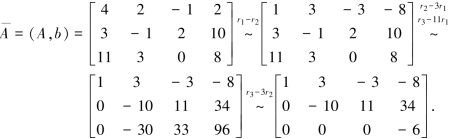
可见,R(A)=2,R(A)=3,R(A)≠R(A).所以方程组无解.
例4.1.3 解非齐次线性方程组

解 对方程组的增广矩阵A施行初等行变换:
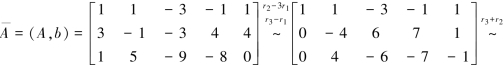

可见,R(A)=R(A)=2<4,因此,方程组有无穷解.
原方程组所对应的同解线性方程组为:
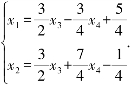
令x3=c1,x4=c2,得
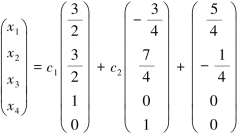
当c1,c2取遍所有实数时,可得到线性方程组的全部解.因此上式称为方程组的通解.任意给定c1,c2的值,都可确定方程组的一组解.如c1=0,c2=0,得x1=
![]()
例4.1.4 λ取何值时,非齐次线性方程组
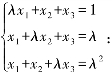
解 解法一 将方程组的增广矩阵施行初等行变换:
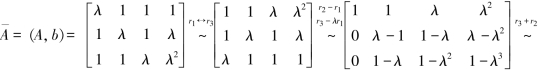
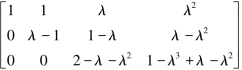
(1)当R(A)=R(A)=3时,即
![]()
(2)当R(A)<R(A)时,即
![]()
(3)当R(A)=R(A)<3时,即
![]()
解法二 由于该方程组的系数矩阵为方阵,故可以用克莱姆法则求解.
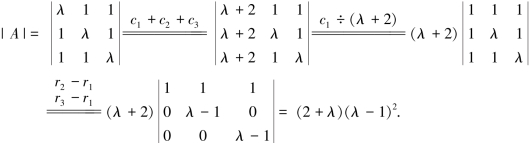
由克莱姆法则知,方程组的系数行列式|A|≠0时,即λ≠-2,λ≠1时有唯一解.
当λ=-2时,
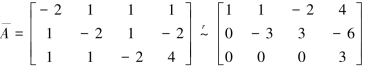
知R(A)=2,R(A)=3,故方程组无解;当λ=1时,
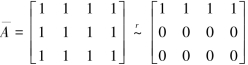
知R(A)=R(A)=1,故方程组有无穷解.
§4.2 齐次线性方程组解的结构
不难验证齐次线性方程组AX=O的解具有如下性质:
性质4.2.1 若ξ1,ξ2均为AX=O的解向量,则ξ1+ξ2也是AX=O的解向量.
这是因为A(ξ1+ξ2)=Aξ1+Aξ2=O.
性质4.2.2 若ξ为AX=O的解向量,k为任意常数,则kξ也是AX=O的解向量.
这是因为A(kξ)=k(Aξ)=k·O=O.
由此可知,若ξ1,ξ2均为AX=O的解向量,k1,k2为任意常数,则k1ξ1+k2ξ2仍为AX=O的解向量,即AX=O解向量的线性组合仍为其解向量.
记S为AX=O全体解向量所构成的集,结合性质4.2.1和性质4.2.2得,S为向量空间,称之为AX=O的解空间.这样,当AX=O有非零解时,只要找到解空间S的一组基,就相当于找到了AX=O的所有解.下面就来寻找解空间S的基.
设AX=O的系数矩阵的秩R(A)=r<n.不妨设A的前r个列向量线性无关,则A的行最简形矩阵为
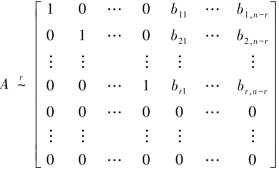
则得到与AX=O同解的线性方程组为

在以上方程组中取定xr+1,xr+2,…,xn的一组值,就唯一确定了x1,x2,…,xr,便得到了齐次线性方程组AX=O的一个解.这里xr+1,xr+2,…,xn为自由未知量,共有n-r个.下面依次取
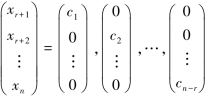
相应得到方程组AX=O的通解:
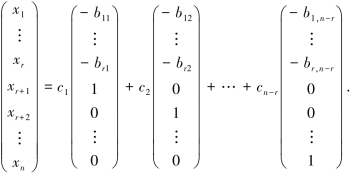
若记
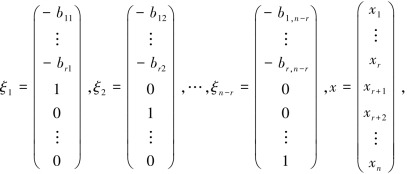
则线性方程组AX=O的通解表示为x=c1ξ1+c2ξ2+…+cn-rξn-r(c1,c2,…,cn-r为任意常数)
由上式可以看出,齐次线性方程组AX=O的任一解向量x∈S都可表示成ξ1,ξ2,…,ξn-r的线性组合,而且容易证明ξ1,ξ2,…,ξn-r线性无关.由定义3.5.1(向量空间基的定义)可知:ξ1,ξ2,…,ξn-r为S的一组基.上述过程提供了一种求解空间S的基的一种方法,而向量空间的基不是唯一的.事实上,S中任意n-r个线性无关的向量都可以作为S的基.
齐次线性方程组解空间S的基称为该齐次线性方程组的基础解系.由上面的讨论可知,要求齐次线性方程组的通解,只需求出它的基础解系.
当R(A)=n时,AX=O只有零解,无基础解系;
当R(A)=r<n时,AX=O必有含n-r个向量的基础解系.
例4.2.1 求齐次线性方程组
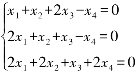
解 将其系数矩阵施行初等行变换:
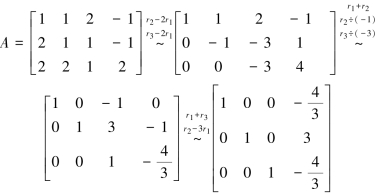
(注意:R(A)=r=3,未知量的个数n=4,因此自由未知量个数n-r=1,也就是该方程组的基础解系中解向量个数为n-r=1个.)
对应的同解线性方程组为
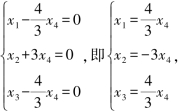

![]()
在这个例子中,也可取其他变量为自由未知量.但不管如何选取,自由未知量的个数总是确定的,自由未知量的个数等于未知量的个数n减去系数矩阵A的秩r.我们规定:自由未知量总是尽可能从后往前取,如本例中取x4为自由未知量.
由上例可得求解齐次线性方程组的步骤:
(1)将其系数矩阵A进行初等行变换化为阶梯型矩阵,判断R(A)与未知量个数n的关系.若R(A)=n则该方程组只有零解,求解完毕;若R(A)<n,则该方程组有非零解.
(2)若方程组有非零解,继续进行初等行变换将行阶梯型矩阵化为行最简型矩阵,找到最简型矩阵对应的同解线性方程组,确定出自由未知量,赋予自由未知量值,进而求出该方程组的通解.
例4.2.2 λ和μ为何值时,齐次方程组
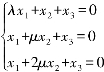
解 由于该方程组的系数矩阵为方阵,故考虑其方阵的行列式:
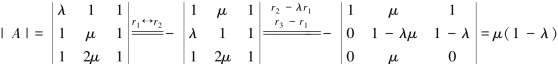
当|A|=0时,即μ=0或者λ=1时齐次方程组有非零解.
§4.3 非齐次线性方程组解的结构
对于n元非齐次线性方程组AX=b,A为其系数矩阵,b≠O,并称AX=O为其所对应的齐次线性方程组.
性质4.3.1 若η1,η2是AX=b的解,则η1-η2是它所对应的齐次线性方程组AX=O的解.
性质4.3.2 若η是AX=b的解,ξ是其所对应的齐次线性方程组的解,则η+ξ是AX=b的解.
由上面的两条性质,得到非齐次线性方程组解的结构.
定理4.3.1 n元非齐次线性方程组AX=b的通解可表示为它的一个特解与其所对应的齐次线性方程的通解之和.
证 设R(A)=r,η∗是AX=b的一个解(即为特解),η是AX=b的任意一个解.由性质4.3.1知,η-η∗=ξ一定为其所对应的齐次线性方程组AX=O的解.从而由齐次线性方程组解的结构知:η-η=k1ξ1+k2ξ2+…+kn-rξn-r,这里ξ1,ξ2,…,ξn-r为AX=O的基础解系,即η=η∗+ξ.这表明AX=b的任意一个解总可表示为它的一个特解与它所对应的齐次线性方程组的通解之和.
证毕.
例4.3.1 解非齐次线性方程组
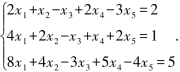
解 将其增广矩阵施行初等行变换:

(R(A)=R(A)=r=2<n=5,原方程组有无穷多个解.)它所对应的同解线性方程组为
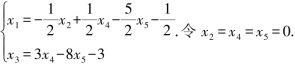
可得方程组的特解为η∗

该非齐次线性方程组所对应的齐次线性方程组为:
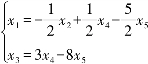
自由未知量的个数=n-r=3,可选x2,x4,x5为自由未知量.令x2=c1,x4=c2, x5=c3,得到齐次线性方程组通解为:
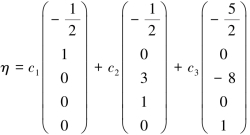
因此该方程组的通解为:

本例中,实际上将最后的行最简型矩阵写成它的同解线性方程组,找到自由未知量x2,x4,x5.令x2=c1,x4=c2,x5=c3,直接可得到方程组的通解,结果和上面是完全一样的,只是没有解的结构的讨论.我们并不知道η∗为这个非齐次方程组的特解,也不知道η为其所对应的齐次线性方程组的解.在以后求解非齐次方程组的通解时,可直接由行最简型矩阵对应的同解方程组写出通解即可.
例4.3.2 设四元非线性方程组的系数矩阵的秩为3,已知η1,η2,η3是它的三个解向量,且η1
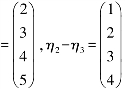
分析 要找到非齐次线性方程组的通解,只需找到它的一个特解与其所对应的齐次线性方程组的基础解系即可.
解 设该方程组为AX=b,η1=
![]()
该方程组所对应的齐次线性方程组的基础解系中含有n-r=1个解向量,因此只需找到一个非零向量ξ,使得Aξ=O即可.
因为Aη2=b,Aη3=b,所以A(η2-η3)=O,记ξ=η2-η3=
![]()
所以,该方程组的通解可表示为
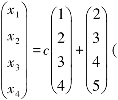
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















