实际光线经共轴球面系统的光路计算公式

2.1.3　实际光线经共轴球面系统的光路计算公式

共轴球面系统通常是由多个折射球面所组成，因此，对于实际光线经共轴球面系统的光路计算，只要将单个折射球面的计算公式，依次重复地应用于每个折射球面即可。这里需要解决的主要问题是，从一个面过渡到下一个面的转面计算。

若共轴球面系统是由m个折射球面所组成，则系统的结构由下列数值所确定：

各折射球面的曲率半径为r₁，r₂，…，r_m；

各球面顶点之间的距离为d₁，d₂，…，d_m－1。其中，d₁系指第一面顶点至第二面顶点之间的距离，d₂系指第二面顶点至第三面顶点之间的距离，依此类推；

各球面间介质的折射率为n₁，n₂，…，n_k，…，n_m，n_m+1。其中，n₁是第一面前方的介质折射率，n₂是第一与第二面之间的介质折射率，依此类推，n_m+1是第m面后方介质的折射率。

给定上述结构参数后，光线的光路计算即可进行。在多个面连续折射成像的过程中，前一个面的像空间就是后一个面的的物空间，因此应有如下各量的转面过渡公式：

例如，系统中第K面的折射应有

第K面与第K+1面之间的转面应为

n_k+1=n_k＇，U_k+1=U_k＇，L_k+1=L_k＇－d_k

光线的光路计算又称为光线追迹或描光路，以下举例说明。

［例2－1］　一双胶合镜组，其结构参数为

　　　　　　　　　　　　　　　　　n=1.0　　　　　（空气）

r₁=67.30mm

　　　　　　　　　　d₁=2.5mm　　　n＇₁=n₂=1.6725　（ZK₂玻璃）

r₂=28.31mm

　　　　　　　　　　d₂=6.0mm　　　n＇₂=n₃=1.5891　（ZK₃玻璃）

r₃=－166.34mm

　　　　　　　　　　　　　　　　　n＇₃=1.0（空气）

若给定入射条件为：L₁=－∞，U₁=0，h₁=12.5，求像方截距L₃＇及像方孔径角U₃＇。

计算格式和过程如表2.1所示。最终计算结果为：像方截距L₃＇=90.836；像方孔径角U₃＇=7.5120°。各中间结果和最终结果见图2.6。

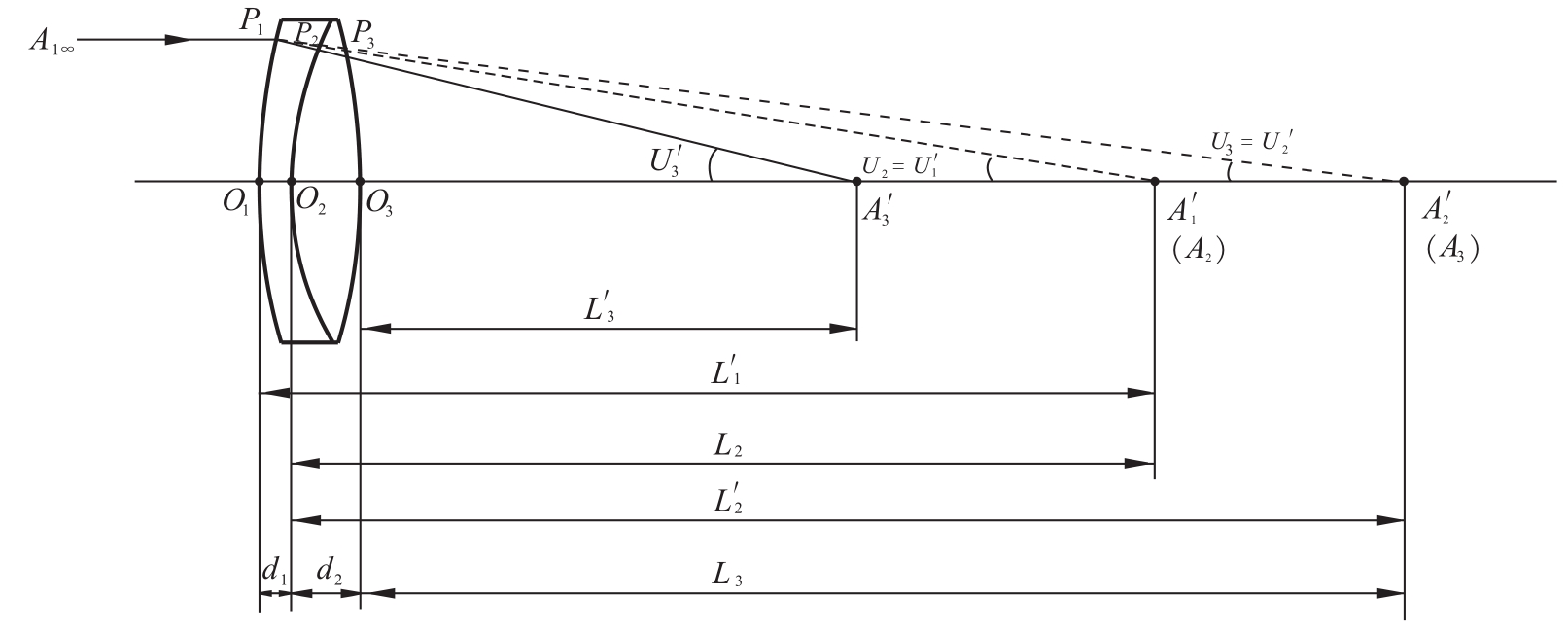
图2.6　双胶透镜的成像过程