物像位置共轭特性曲线

3.5.1　物像位置共轭特性曲线

由牛顿公式xx＇=ff＇以及xx＇=－f＇²（n＇=n）可以看出，对折射系统，在给定焦距的情况下，应有xx＇=ff＇=k＜0。

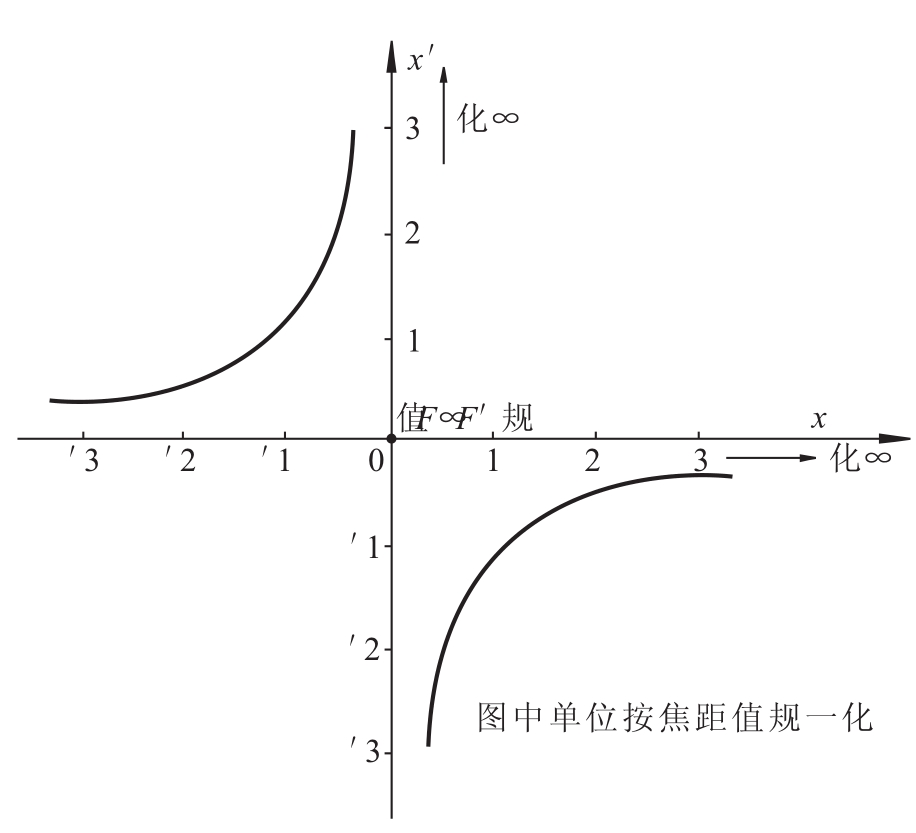
图3.19　牛顿方程曲线

上式中k为小于零的常数，因此像距x＇与物距x之间为双曲线函数关系，即物象共轭位置的特性曲线是由分布在Ⅱ、Ⅳ象限的两条双曲线（或称双曲线对）组成，可以称之为牛顿方程曲线（见图3.19）。该特性曲线表明，当物距x由－∞→0时，其共轭像距x＇则由0→+∞；当物距x由0→+∞时，则像距x＇由－∞→0。图中的坐标原点0，对物距来说，相当于物方焦点F；对像距来说，相当于像方焦点F＇。牛顿方程曲线不论对正透镜（正光组）还是负透镜（负光组）均适用。但是曲线的具体形状是与系统的焦距值有关的，当光学系统（透镜）的焦距不同时，其对应的双曲线对的形状也不同，因而不同焦距的系统，其物像位置共轭特性曲线是一系列双曲线对簇。

牛顿方程曲线反映了物像位置共轭关系的基本规律，但不能明确地反映物像的虚实等情况。因此，通常更多地以高斯方程曲线的形式来反映物像位置共轭关系的规律。

高斯方程曲线与牛顿方程曲线本质相同，是同一个双曲线对，仅坐标选取不同而已。由于两种公式系之间的物距以及像距分别存在如下关系：l=x+f　l＇=x＇+f＇，因此高斯方程曲线可以视为牛顿方程曲线中的坐标轴分别沿横轴方向平移f，沿纵轴方向平移f＇而成。

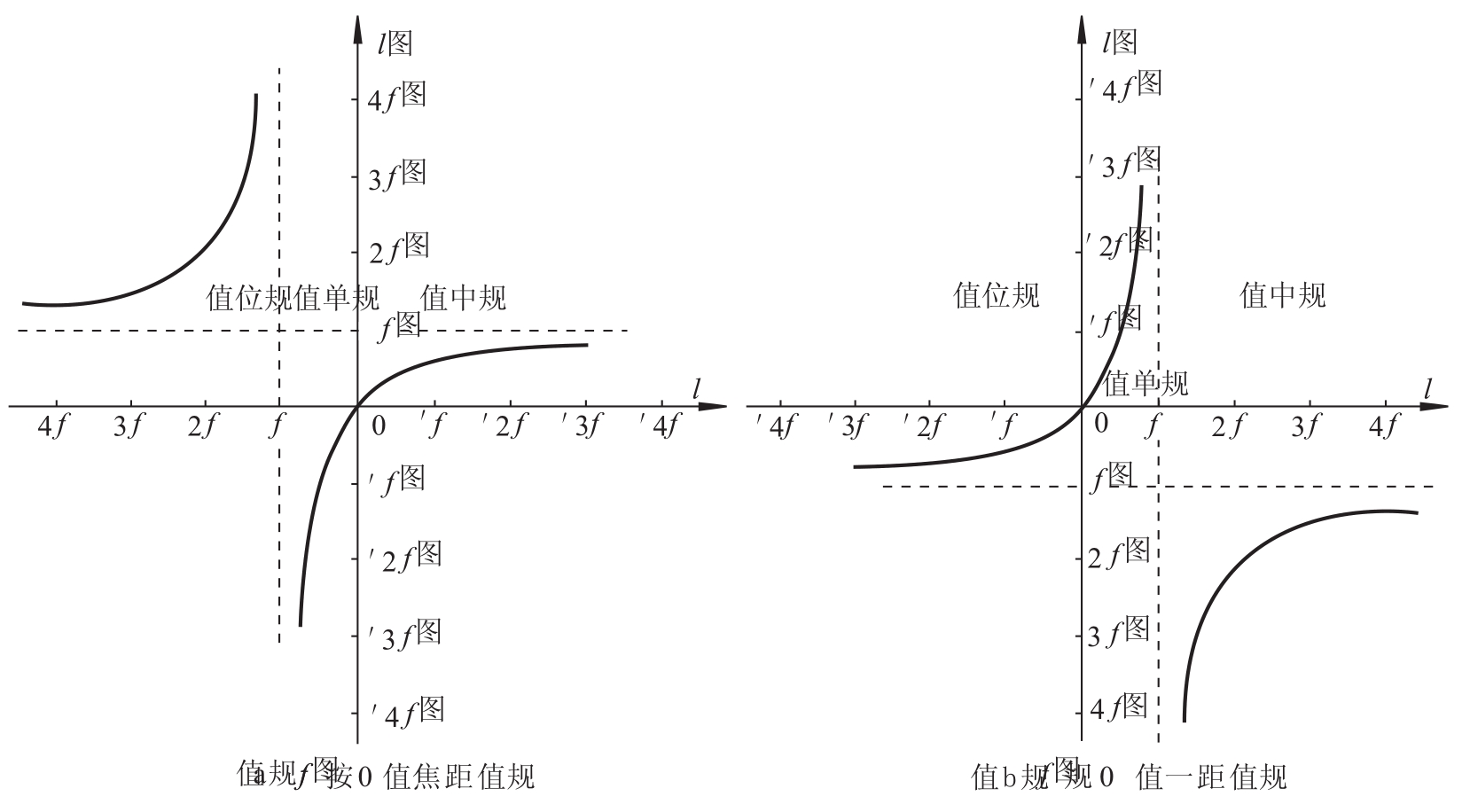
图3.20　高斯方程曲线

图3.20（a）和（b）分别给出了正透镜（正光组）和负透镜（负光组）的高斯方程曲线，从分析物像虚实性的角度考虑，可以将成像规律都按如下三个区间来划分：

正透镜（正光组）　　　　　　　　　　　　　　　　　　　负透镜（负光组）

区间（Ⅰ）－∞＜l＜f，实物成实像；　　　　区间（Ⅰ）－∞＜l＜0，实物成虚像；

区间（Ⅱ）f＜l＜0，实物成虚像；　　　　　区间（Ⅱ）0＜l＜f，虚物成实像；

区间（Ⅲ）0＜l＜+∞，虚物成实像。　　　　区间（Ⅲ）f＜l＜+∞，虚物成虚像。