截距计算法

3.9.2　截距计算法

式（3.82）亦可以表为如下形式：

由于，又因

h₂=l₂tanU₂=l₂＇tanU₂＇，

h₃=l₃tanU₃=l₃＇tanU₃＇，

…　　　　　　　　　　　　

h_k=l_ktanU_k=l_k＇tanU_k＇，

将上述比例关系代入前式，则得到

用这种方法求复合系统的像方焦距，只需令l₁=－∞，然后连续应用高斯公式和过渡公式，求出各光组的物距和像距，代入式（3.91）即可。由于是利用截距计算焦距，故称截距计算法。必须注意，式（3.91）仅当l₁=－∞时才适用。相应地，像方焦点位置l_F＇=l_k＇；像方主面位置l_H＇=l_F＇－f＇。

［例3－5］　利用正切计算法和截距法计算［例3－4］中所给定结构的像方基点位置和焦距并与前面计算结果相校核。

解：（1）正切计算法：

令tanU₁=0，并取h₁=f₁＇=40。

按式（3.87）的过程计算，应有

tanU₂=tanU₁＇===1，h₂=h₁－d₁tanU₁＇=40－20×1=20，tanU₂＇=tanU₂+= 1+=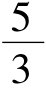，又由式（3.81）～（3.83）式，应有结果：

l_F＇=l₂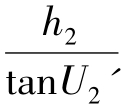＇===12，f＇===24，l_H＇=l_F＇－f＇=12－24=－12

（2）截距计算法

令l₁=－∞，由高斯公式应有

l₁＇=f₁＇=40，l₂=l₁＇－d₁=40－20=20，l₂＇===12

将上述计算结果代入式（3.91），得到

f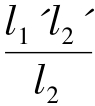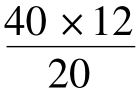＇===24，l_F＇=l₂＇=12，l_H＇=l_F＇－f＇=12－24=－12

上述计算结果表明，利用正切计算法与截距计算法得到的结果与用组合公式法计算结果完全一致。这种光路计算的方法，对多光组复合的计算其优越性将更为明显。