【摘要】：如图5.18，设平面镜Q1Q1绕垂直于图平面的轴线O转过α角到达Q2Q2，平面镜在O点处的法线由N1转至N2。在距转轴O为r处有一发光点S，需考察：当入射光线SO不变时，反射光线有何变化?由此可得出结论：当平面镜绕转轴O转动时，像点将在以O为圆心、以r=OS为半径的圆周上，以二倍于平面镜的转速绕O轴转动。平面镜的旋转效应在光学仪器中有很多应用。
5.4.2 平面镜的旋转效应
如图5.18，设平面镜Q1Q1绕垂直于图平面的轴线O转过α角到达Q2Q2，平面镜在O点处的法线由N1转至N2。在距转轴O为r处有一发光点S，需考察：当入射光线SO不变时，反射光线有何变化?另外，发光点S的像点有何变化?
若OS1为平面镜初始位置为Q1Q1时的反射光线，OS2为平面镜绕O轴转过α角后之反射光线，由反射定律可以导出平面镜转过α角后反射光线OS2与OS1之间的角度（β～α）关系：
I2=I1+α
β=2I2－2I1=2α （5.33）
由此可得出结论：当平面镜绕垂直于入射面的轴线转动α角时，反射光线将按同一方向转动2α角。
若S＇为平面镜初始位置Q1Q1时S的像点，则S＇与S对Q1Q1对称，且有OS＇=OS=r，即S＇与S同在以O点为圆心、以r为半径的圆周上；当平面镜转动α角后，由转动2α角的反射光线OS2的延长线决定的像点S″与S点对平面镜Q2Q2对称，且有OS″=OS=r，即S″点与S、S＇点在同一圆周上。由此可得出结论：当平面镜绕转轴O转动时，像点将在以O为圆心、以r=OS为半径的圆周上，以二倍于平面镜的转速绕O轴转动。
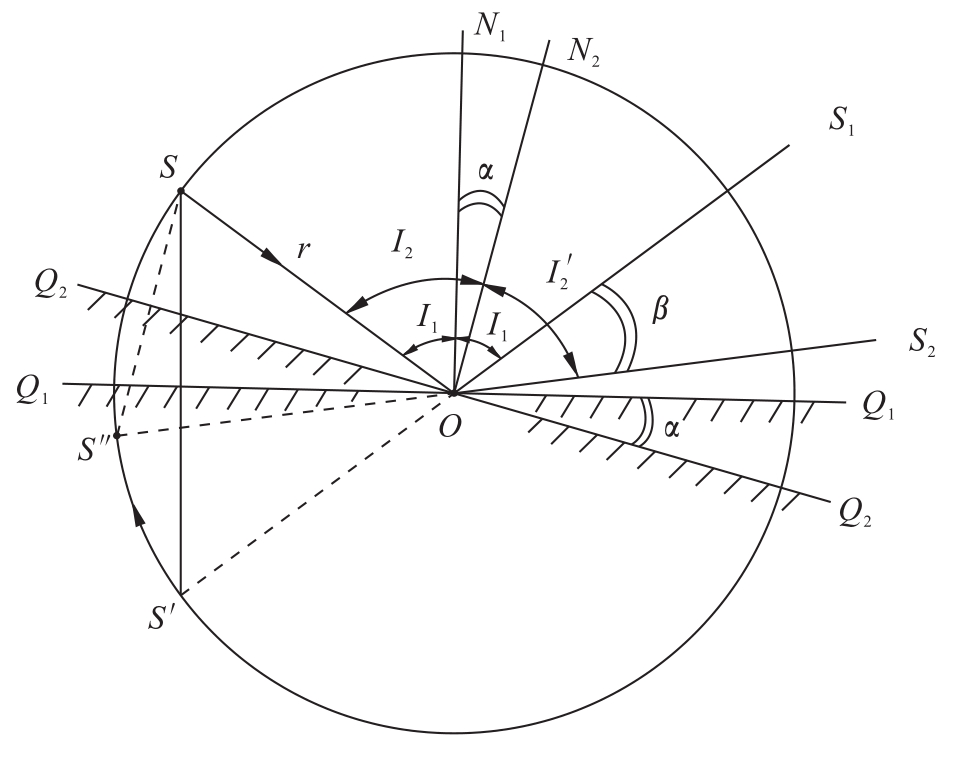
图5.18 平面镜的旋转效应
平面镜的旋转效应在光学仪器中有很多应用。例如：一些军用观测瞄准仪器为了瞄视水平和高低不同方位的目标，常在头部设置可绕竖直轴线和水平轴线转动的平面镜或反射棱镜；周视瞄准镜中用于补偿头部棱镜绕垂直轴线转动引起的像面偏转影响的梯形棱镜；测量棱镜角度偏差的自准直望远镜原理以及光学比较仪中的光学杠杆原理等。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
