矢量形式的反射定律

5.7.1　矢量形式的反射定律

如图5.42所示，若矢量A是空间任意的非单位矢量，则对其相关的数学表示形式与物理意义首先作如下规定：

（1）以光线传播方向的单位矢量表示该光线的方向。例如，以A°表示入射光线的单位矢量；以A°＇表示反射或折射光线的单位矢量；

（2）以反射面或折射面在光线入射点处小面元的法线方向单位矢量N表示反射面或折射面的位置，其方向迎向入射光线；

（3）采用右手直角坐标系，沿三坐标轴ox、oy、oz方向的单位矢量分别为i、j、k，矢量A与三坐标轴夹角的方向余弦分别为：cosα、cosβ、cosγ。

则应有

A=A_xi+A_yj+A_zk　　　　　　　　　　　　（5.54）

式中A_x、A_y、A_z为矢量A在ox、oy、oz三轴上的投影；由于A°为A的单位矢量，即│A°│=1，而α、β、γ为矢量的方向角，则应有

A°=cosαi+cosβj+cosγk　　　　　　　　　　　　（5.55）

因而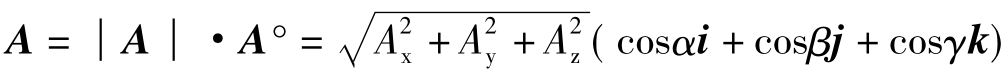　　

但应指出，在应用矢量计算方法研究物像空间变换问题时，为了计算的简化（便于验算），实际均取各矢量（即A、A＇、N）为单位矢量进行计算。

图5.42　任意空间矢量的表示形式

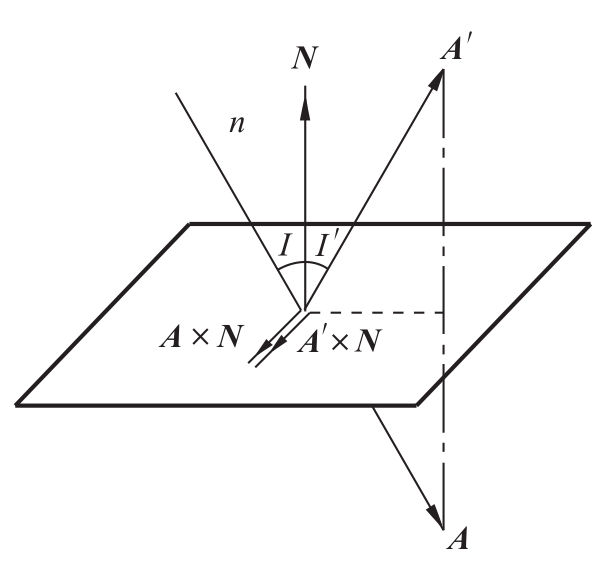
图5.43　第一反射定律图示

1）反射定律的矢量表示形式之一

反射定律可以用一个矢量方程式来表示：（^*1）

A×N=A＇×N　　　　　　　　　　　　　　　（5.56）

上面矢积的等式是矢量A、A＇与N共面的条件。反射定律的这种矢量表示形式又称为第一反射定律，其物理意义是：矢量A×N（垂直于A和N所决定的平面——入射面）与矢量A＇×N（垂直于A＇和N所决定的平面——反射面）两者方向一致，因而A、N、A＇三者共面；并且其大小相等（见图5.43）。

由式（5.56）的数量关系，应有：

│A×N│=│A││N│sin（A，N）=sin（180°－I）=sinI

│A＇×N│=│A＇││N│sin（A＇，N）=sinI＇

两者相等，因而有　I=I＇

上式中I与I＇均为绝对值，而不表示方向。这就是反射定律的数量表示形式，又称为第二反射定律。

2）反射定律的矢量表示形式之二

式（5.56）表达了反射定律的基本概念，但不便于计算。由于希望解决根据已知的A、N，计算反射光线A＇，确定其具体的空间方位，即需导出以A、N表示的A＇表达式。为此需运用如下三重矢积的一般展开公式

A×（B×C）=B（A·C）－C（A·B）

首先用N对第一反射定律式（5.56）两边作矢积运算并展开，依次应有

N×（A×N）=N×（A＇×N）

A（N·N）－N（A·N）=A＇（N·N）－N（A＇·N）

A＇=A+N（A＇·N）－N（A·N）　　　　　　　　（5.57a）

然后，同样用A、A＇对式（5.56）两边作矢积运算，分别得到N的如下两种结果表达式：

N=（A－A＇）（A·N）+N（A·A＇）　　　　　　（5.57b）

N=－（A－A＇）（A＇·N）+N（A＇·A）　　　　（5.57c）

比较式（5.57）（b）、（c）两式，得到

（A－A＇）（A·N）=－（A－A＇）（A＇·N）

由于A－A＇≠0，所以上式两端可约去（A－A＇），因而有：

A＇·N=－A·N　　　　　　　　　　　　　　　（5.57d）

将式（d）代入式（a），得到

A＇=A－2（A·N）N　　　　　　　　　　　　　　（5.58）

上式是反射定律的第二种矢量表示形式。由于数量积的运算形式简单，因而上式非常重要且便于计算：如果已知A、N，则可以方便地算出A＇；反之，若给定A、A＇，也可以方便地求出反射面的法线矢量N，即决定反射面的空间方位。若将式（5.58）的两边分别与矢量A作标积，则得到

A·A＇=1－2（A·N）²

由上式可求得标积A·N，它也就是已知的矢量A和N之间夹角的余弦（由于该角大于90°，因而下式根号前应取“－”号）：

*注（*）本节内的“×”均表示矢积的叉乘运算

将上式代入（5.58）式，则可求得法线矢量N：