矢量形式的折射定律

5.7.2　矢量形式的折射定律

1）折射定律的矢量表式形式之一

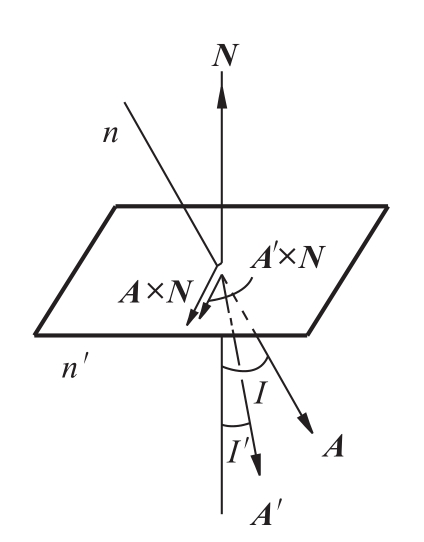
图5.44　矢量形式折射定律

在前述规定下，若介质两边折射率分别为n和n＇，则折射定律可表为如下的矢量方程形式（见图5.44）：

n（A×N）=n＇（A＇×N）　　　　　　　　　　　　（5.61）

折射定律的这种矢量表示形式又称为第一折射定律。上式表明：A、A＇和N三者共面，即矢量A×N与A＇×N方向一致；其数量关系应为

n│A×N│=n＇│A＇×N│

上式中，n│A×N│=n│A││N│sin（A，N）=nsin（180°－I）=nsinI；n＇│A＇×N│=n＇│A＇││N│sin（A＇，N）= n＇sin（180°－I＇）=n＇sinI＇。

代入前式，则得到式（1.3）的折射定律形式：nsinI=n＇sinI＇

上述折射不变量的数量关系又称为第二折射定律。

2）折射定律的矢量表示形式之二

为了建立便于直接计算A＇的矢量表达式，将式（5.60）两边同与N作矢积运算，并按三重矢积展开，依次应有

nN×（A×N）=n＇N×（A＇×N）

n［A（N·N）－N（N·A）］=n＇［A＇（N·N）－N（N·A＇）］

n［A－N（A·N）］=n＇［A＇－N（A＇·N）］　　　　　　　　　　（5.62）

上式即为折射定律的第二种矢量表示形式。其中：

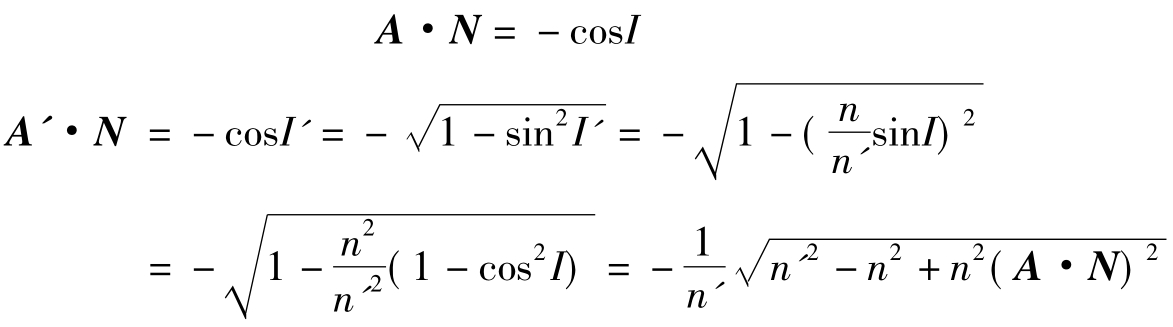
若将上两式代入式（5.62）并整理即得到

因此，如果知道A、N，代入上式即可方便地求出折射矢量A＇。

需要特别指出的是，对于能展成平行平板玻璃的反射棱镜，考虑入射面和出射面两次折射及相关反射的计算结果与不考虑2个折射面的折射而只考虑反射的计算结果完全一致。这是由于平行平板玻璃的两次折射不改变光轴的方向与物像方位的特性所决定的。这一结论对所有能展成平行平板玻璃的反射棱镜均有效，因此，今后计算光线经反射棱镜的结果，只需依次计算其中各反射面的反射作用即可，从而使计算大为简化。