物空间在平面上成像的清晰深度

7.7　物空间在平面上成像的清晰深度——光学系统的景深

理想光学系统的成像理论指出，物空间的一个平面在像空间有唯一的平面与之共轭。迄今为止所讨论的实际光学系统成像问题，基本上是垂直于光轴的共轭物像平面上点的成像问题。属于这一类成像情况的光学系统，有电影放映物镜、幻灯投影物镜、照相制版物镜以及某些类型的显微镜等；实际上，更多的系统需要将一定深度范围的物空间成像在一个平面上，称这种像为“平面上的空间像”。这一类系统有照相物镜、望远镜以及眼睛等。当然，这些成像仅当实际光学系统具有光阑，此光阑限制光束、且使光束变得很细时，才有可能。

应该指出，平面物体的成像与物空间所成的平面像两者是有区别的。对于前者，物、像平面之间满足严格的共轭关系，在理想成像的条件下，像面上所有点均为清晰的点像；对于后者，像平面上除了映出与其共轭的物平面的像之外，同时还映出了位于共轭物平面前后的空间点的像。但是，这些非共轭点在像平面上所成的像，不再是点像，而是一些相应光束的截面——弥散斑。当这些弥散斑的截面积足够小，满足一定的条件时，可以将其等价地视为深度物点的共轭像，并认为所成的像是“清晰的”。下面将讨论像面上获得清晰像的物空间深度范围，并导出景深的概念。

如图7.20所示，P为系统的入瞳中心，P＇为出瞳中心。设过轴上物点A的垂轴平面为“对准平面”（或称基准平面），过轴上像点A＇的垂轴平面为其共轭的像平面，称为“景像平面”。B₁、B₂是位于对准平面前后的空间点，B₁＇、B₂＇分别为其共轭像点，且均在景像平面之外。严格讲，对准平面与景像平面是一对共轭平面。因此，只有对准平面上的点才能在景像平面上成点像；而位于对准平面外的空间点B₁、B₂在景像平面上形成的弥散斑Z₁＇、Z₂＇，则是由光束B₁＇P₁＇P₂＇与B₂＇P₁＇P₂＇在景像平面上的截面所决定的，称Z₁＇、Z₂＇为B₁＇、B₂＇在景像平面上的“投影像”，它们分别与物空间相应光束B₁P₁P₂和B₂P₁P₂在对准平面上的截面Z₁、Z₂相共轭。

从实用的观点看，纯几何意义的“点像”是毫无意义的。由于光学系统的成像总是要被接受器所接受，而接受器（例如眼睛、感光底片等）都不是十分完善的，因此可以根据接受器的特性，按照成像质量的要求，规定空间点在景像平面上弥散斑大小的允许数值。例如，若接受器为人眼，当弥散斑对眼睛的张角小于眼睛的最小分辨角（约1＇）时，则眼睛看起来并无不清晰的感觉。这样，就可以视该弥散斑为空间点在平面上所成的“点”像；由这样的一些弥散斑所组成的像面是清晰的，并称这样的像面为“空间的平面像”（或称“平面上的空间像”）。由图可见，空间点在景像平面上所成像的位置，可由各空间点的主光线与像平面的交点决定。对于不同的光能接受器以及不同用途的系统，将有不同的弥散斑大小的允许数值。

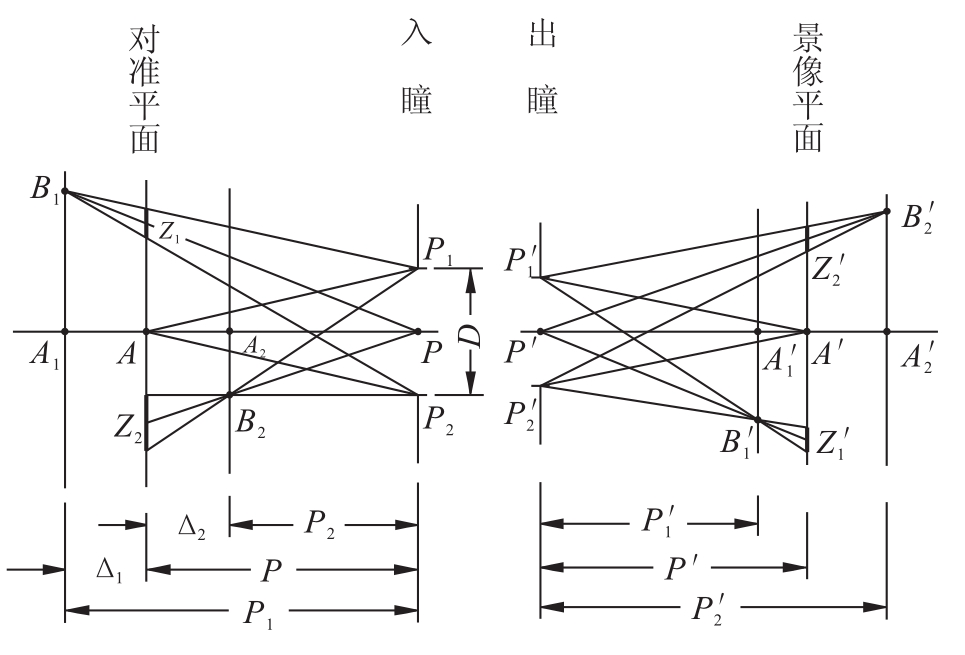
图7.20　对准平面及其前后空间点在景像平面上的成像

下面分析空间点在景像平面上形成的弥散斑大小与哪些因素有关。由图7.20可见，景像平面上的弥散斑Z₁＇、Z₂＇分别与对准平面上的弥散斑Z₁、Z₂共轭。若Z和Z＇分别表示弥散斑直径，且知共轭平面A与A＇之间的横向放大率为β，则应有

Z₁＇=βZ₁，Z₂＇=βZ₂

由图中的相似三角形关系，可以得到：

将上述关系代入前式，则得到：

上式表明，景象平面上的弥散斑大小Z₁＇和Z₂＇，除与入瞳直径D及共轭面处的横向放大率β有关外，尚与空间点及对准平面至入瞳的距离P₁、P₂和P有关。在入瞳直径确定的前提下，可以根据不同的光能接受器所允许的弥散斑的最大值Z₁＇、Z₂＇（即可以认为是清晰点像的临界值），确定像平面上能获得清晰像的物空间深度范围。

定义能在像面上获得清晰像（物点所成的弥散圆不能被接受器所分辨）的物空间深度为“景深”，以Δ表示。其中，能成清晰像的最远平面称为“远景”；能成清晰像的最近平面称为“近景”。对准平面、远景和近景至入瞳的距离分别以P、P₁和P₂表示；在像空间，各共轭平面至出瞳的距离分别以P＇、P₁＇和P₂＇表示。远景和近景至对准平面的距离称为“远景深度”和“近景深度”，并分别以Δ₁和Δ₂表示。并认为弥散斑的直径总为正，因而上述所有量值均视为正值，即取绝对值（图中均标注正值）。显然，各量之间应有如下关系：

Δ₁=P₁－P，Δ₂=P－P₂；且Δ=Δ₁+Δ₂

即景深等于远景深度与近景深度之和。

由于不同系统所允许的弥散斑大小不同，因而以下结合照相机物镜和望远系统两种典型系统，讨论其景深（或远景及近景的空间深度）与各有关量之间的关系。