单位及其换算关系

8.1.7　光度学各主要光度量名称、单位及其换算关系

为了全面理解及使用方便，现将光度学中各主要光度量的名称、定义、单位及其换算关系列表如后（见表8.10）。

表8.10　主要光度量的名称、符号定义方程和单位

［例8.4］　采用功率为250W、发光效率为30lm/W的卤钨灯作为光源，通过一个焦距与口径均为100mm的聚光镜去照明前方12m处的圆屏，屏的直径为2m，求聚光后的发光强度以及圆屏上的平均光照度。若用该卤钨灯直接照射该屏，其平均光照度应为多大?（假定该卤钨灯可视为各向均匀发光的点光源）

解：该照明系统如图8.15所示。

图8.15　照明系统光路图

（1）计算确定光源的位置

光源的位置应使它发出的光束（光锥角为u）经聚光镜后（光锥角为u＇），恰能在聚光镜前方12m处生成直径为2m的圆面积。根据给定条件，可求出聚光镜的像方光锥角u＇：

由正切计算公式，应有

由上述光束变换分析，可求得灯泡A的位置：

（2）求光源经聚光镜成像前后的照明立体角

由孔径角与立体角之间的转换式（8.5），可求光源A对聚光镜构成的立体角为

光源像A＇对圆屏所构成的立体角为

（3）计算光源在聚光镜前后的发光强度

卤钨灯发出的总光通量为

φ_v=ηp=30×250=7500（lm）

假定卤钨灯可近似视为各向均匀发光的点光源，它在聚光镜前的发光强度为

光源发出的总光通量中能通过聚光镜的部分为

φ_ω=I_vω=596.83×0.8462=505（lm）

忽略经聚光镜的光能损失，即经聚光镜后光束的立体角变为ω＇，但光通量不变，应有

φ_ω=φ_ω＇=I＇ω＇=505（lm）

因而可求出经聚光镜后的发光强度为

计算表明，光源经聚光镜后，虽光通量未变，但由于ω＇大大减小，光能重新分配，故I＇大大增强。

（4）计算被照圆屏上的平均照度

被照明的圆面积为：A=πr²=π×1²=3.1416（m²）

圆面积上的平均光照度为。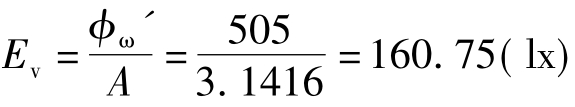

（5）对比光源直接照明圆屏（不加聚光镜）的效果：

光源对圆屏所构成的光锥角α为

对应的立体角为

被照圆屏上所接受的光通量为

φ_Ω=IΩ=596.83×0.0214=12.77（lm）

圆屏上的平均照度为：

上述计算与比较表明，在照明系统中加入聚光镜后，可使被照明平面上的照度得到显著提高（本例照度增强近40倍），因而体现了照明系统中聚光镜的重要作用。