望远系统的外形尺寸计算举例

10.7.2　望远系统的外形尺寸计算举例

按照转像系统构成的不同，望远系统基本可分为具有棱镜转像系统的望远系统和具有透镜转像系统的望远系统两种类型。两类系统的外形尺寸计算特点各有不同，现分别举例计算分析如下。

1）具有棱镜转像系统的望远系统外形尺寸计算

利用棱镜转像系统的大量军用观测仪器（如棱镜式双筒望远镜、炮队镜以及各种类型的测距仪等），均可视为在普通开普勒望远镜中加入棱镜转像系统。棱镜转像系统在光路中的作用是折转光轴和正像，若将棱镜展开，则相当于在开普勒望远镜的光路中加入了一块平行平板玻璃。

用棱镜转像的望远系统的外形尺寸计算，通常分两步进行：即首先根据给定的光学性能指标（Γ、2ω、D＇、l_z＇和α等），计算开普勒望远镜的外形尺寸（物镜的焦距和通光口径，目镜的焦距、直径，分划板的直径等）；然后计算确定棱镜及反光镜的尺寸。

下面以军用八倍炮队镜为例，介绍具有棱镜转像系统的望远系统外形尺寸计算方法。

（1）给定的光学性能要求

放大率Γ=8×；视场2ω=7°；出瞳直径D＇=5mm；出瞳距离l_z＇=19mm；潜望高H= 250mm。

（2）拟定光学系统的结构原理图

分析：炮队镜是炮兵观测仪器，因此应采用带分划板的开普勒望远系统，物镜及目镜均具有正光焦度；系统应成正像，为此需加入实现正像的完全转像系统；考虑到仪器要求的潜望高不大（H=250mm），宜采用棱镜转像系统。从减小仪器尺寸、重量使结构紧凑出发，选取靴形屋脊棱镜FX_J－90°与头部反光镜相配合，实现光轴折转与完全转像；在此共轴球面系统与平面系统的组合中，由于头部反光镜要作高低俯仰，故应将其置于平行光路中。为此，物镜应放在头部反光镜与靴形屋脊棱镜之间。光学系统的基本原理结构如图10.19所示。

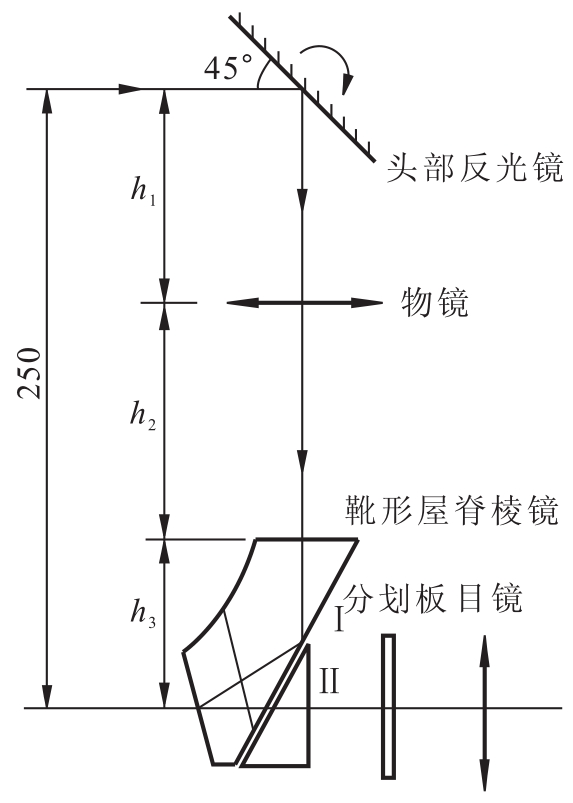
图10.19　炮队镜光学系统基本原理结构图

（3）外形尺寸计算

计算中各光组均按无限薄透镜进行计算。另外，为了减小整个系统的横向尺寸及减小边缘视场像差校正难度，取边缘视场斜光束的渐晕系数K=0.5。

①目镜的选型与参数计算：目镜选型应考虑满足给定的视场及出瞳距离等要求。

已知Γ=－8×，ω=3.5°，将其代入式（6.29），得到：

tanω＇=|Γ|tanω=8×tan（3.5°）=0.489301；ω＇=26.07°

即要求的目镜视场为：2ω＇=52.14°。

考虑到大视场目镜有正畸变，需将计算出的视场增大，若按增加8％计算，应有

2ω＇=52.14°（1+8％）=56.31°

由于要求目镜的视场较大，且出瞳距离也较大（l_z＇≥19mm），因此，可选取表10.2中的艾尔弗Ⅱ或广角目镜。考虑到结构尺寸的小型化，选取广角目镜型。

对一般望远系统，通常将物镜框作为孔径光阑亦即入瞳。根据牛顿公式，出瞳距离l_z、目镜的像方顶焦距l_F＇与目镜焦距f＇之间应有如下关系（见图10.20）：

图10.20　目镜设计选型的分析

式中f₁＇和f₂＇分别为物镜和目镜焦距，Γ为望远系统的视放大率。根据表10.2，取l_F＇= 0.8f₂＇，并将Γ=－8×（先不考虑棱镜系统的倒像作用）、l_z＇=19mm代入式（10.26），解出：

f₂＇=20.54mm

根据计算结果f₂＇=20.54mm、2ω＇=56.31°以及出瞳直径的要求D＇=5mm，可以选用已设计定型的目镜。在选用时，如果焦距值相差很小，即可直接选用；如果焦距值相差较大，则在设计中可以按焦距进行缩放。对本系统，可选用《光学仪器设计手册》P259编号为2－28的目镜。由于焦距值相差很小，故可直接采用该组光学与结构数据。其主要性能参数为

f₂＇=20.216mm，2ω＇=57°，l_F=－4.49mm，D＇=5.0mm

应该注意的是，手册目镜表中的光学特性和结构参数是按反向光路计算给出的。表中的物方量对应于实际目镜的像方量；反之，表中的像方量对应于实际目镜的物方量。

②物镜参数的计算与选型

由式（6.29）知，应有物镜焦距：

f₁＇=－Γf₂＇=8×20.2=161.6（mm）

设入瞳与物镜框重合，则由（6.31）式，应有物镜的通光直径D₁为

D₁=D=|Γ|D＇=8×5=40（mm）

物镜的相对孔径为

另外，要求物镜视场2ω=7°，视场不大。

图10.21　入瞳与物镜框不重合时D₁的计算

根据上述计算结果和要求，参考表10.1，可选择双胶透镜组形式作为本系统的物镜。

应该指出，当入瞳与物镜框不重合时，物镜的通光直径D₁将不等于入瞳直径D，其关系式如图10.21所示，应为

D₁=2l_ztanω+KD　　　　　　　　　　　　　（10.27）

式中：l_z——入瞳距离；

　　　K——边缘视场斜光束的渐晕系数，K≤1。

如果按上式算出的D₁＜D，则应取物镜的直径D₁=D，以保证轴上光束不被切割。

③目镜通光直径D₂的计算

如图10.20所示，在渐晕系数K=0.5的条件下，应有目镜的通光直径：

　　　　　　　　D₂=2（f₁＇+f₂＇）tanω+KD＇

　　　　　　　　　=2（161.6+20.2）×tan3.5°+0.5×5=24.74（mm）

凑整取D₂=25mm。

④分划板直径D_r的计算

由图10.20可知，分划板直径应为

D_r=2f₁＇tanω=2×161.6×tan3.5°=19.77（mm）

由以上计算即可确定构成炮队镜基础的开普勒望远系统的基本外形尺寸。应该指出，外形尺寸计算的顺序并不是一成不变的，而是要根据具体仪器和给定的条件具体分析、灵活运用。本例是从确定目镜的型式和参数开始，计算到物镜；有些情况下，则宜于首先确定物镜的参数和型式，再计算目镜、分划板等各有关量。

⑤头部反光镜尺寸的确定

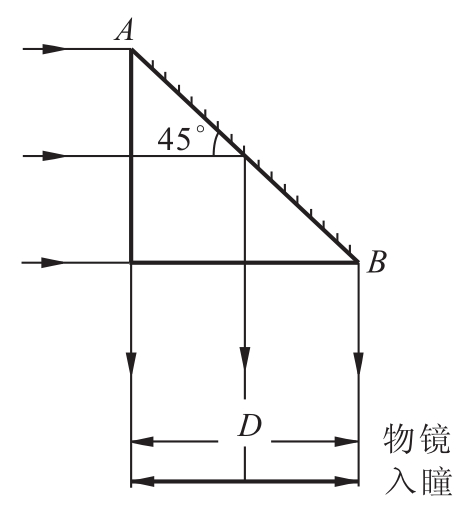
图10.22　头部反光镜的计算

头部反光镜的尺寸应根据能通过系统的轴上及最大视场斜光束宽度的要求来确定。对本系统，边缘视场的渐晕系数K=0.5；另外，物方视场角较小。因此，综合比较，反光镜的尺寸应由轴上有效光束的宽度D决定。如图10.22所示，反光镜的宽度等于物镜的直径D，反光镜的长度应为

因此，反光镜的尺寸为56.57mm×40mm。

⑥靴形屋脊棱镜尺寸的计算

在拟定了光学系统原理图，选定棱镜结构型式后，需要进一步确定棱镜的结构尺寸。由5.5知，棱镜理论结构尺寸计算的核心问题是求出棱镜的通光直径。求出通光直径后，即可利用《光学仪器手册》上册中的表5.9，查出棱镜的展开光路长及其全部结构尺寸。

在已知轴上光束（D=40）和斜光束进行情况（ω=3.5°，K=0.5）的条件下，确定棱镜通光直径的步骤是：首先根据结构所要求的棱镜出射面到分划板的距离a（本例中要求a= 45mm），求出棱镜出射面的通光直径D_Ⅱ；根据D_Ⅱ求出棱镜的光路长L（亦即平行平面玻璃板的厚度d）；然后在选定玻璃的条件下，将d转化为等效空气层厚度e，进而求出棱镜入射面的通光直径D_Ⅰ，并将D_Ⅰ和D_Ⅱ作比较，验算在入射面上是否会产生光束切割现象，以最终确定棱镜的通光直径D_P。

图10.23　棱镜通光孔径的确定

（a）确定棱镜出射面的通光直径D_Ⅱ

如图10.23所示，已知结构要求a=45mm，为确定棱镜出射面的通光直径D_Ⅱ，必须根据图中几何关系，分别计算由轴上光束所决定的通光直径D_Ⅱo和轴外斜光束（a光线）所决定的通光直径D_Ⅱa，比较两者的大小，选取较大者作为棱镜出射面上的通光直径。如图应有

为确定D_Ⅱa，首先需求出a光线与光轴的夹角ω_a：

即　　　　ω_a=0.0425°，因而有

　　　　　　D_Ⅱa=2（f₁＇－a）tan（－ω_a）+KD

　　　　　　　　=2（161.6－45）×（－0.00074257）+0.5×40=19.83（mm）

比较D_Ⅱo＜D_Ⅱa，显然棱镜出射面上的通光直径应由斜光束的a光线决定。凑整取出射面通光直径为20mm，再考虑固定，取棱镜出射面的通光直径为D_Ⅱ=22mm。

（b）根据D_Ⅱ=22mm，查《光学仪器手册》上册P91，得到靴形屋脊棱镜FX_J－90°的光程长（亦为平行平面玻璃板厚度d）：

L=2.980D_Ⅱ=65.56（mm）=d

（c）选择棱镜的玻璃材料

在将平行平面玻璃板的厚度d转换为等效空气板的厚度e之前，必须首先选定棱镜的玻璃材料。棱镜玻璃材料选定的重要因素是考虑反射面上能否产生全反射，并尽可能采用性能好的常用玻璃。

试选最常用的K₉玻璃，已知其全反射临界角

根据5.5节中关于反射棱镜视场角的计算方法，由于在反射面I上（见图10.19），该面的法线与光轴的交角β=60°，且满足90°－β＞β－I₀，因而按照式（5.35）可求出由I面所决定的反射棱镜视场角为

ω=sin^－1［nsin（β－I₀）］=sin^－1［1.5163×sin（60°－41.26°）］=29.15°

ω₀值也可由《光学仪器手册》上册表5.4“棱镜的视场角与玻璃材料的关系”中查到。

在确定了ω₀之后，需要验算射至棱镜入射面上的所有光线中最大入射角I_max是否小于棱镜的视场角ω₀，以确定所有能射入棱镜的光线是否均能在反射面I获得全反射。为此，需计算比较两条光线在棱镜入射面上的入射角（见图10.23），即轴上光束边缘光线在棱镜入射面上的入射角U_m＇和最大视场斜光束的b光线在棱镜入射面上的入射角ω_b。如图应有

比较U_m＇和（－ω_b），显然最大入射角I_max=7.055°，并且有I_max＜ω₀，因此，射入棱镜的所有光线在反射面I上均能获得全反射。这也表明棱镜材料的选择是合适的。

（d）计算棱镜入射面的通光直径D_Ⅰ

厚度为d的平行平面玻璃板的等效空气板厚度为

由图10.23可求得轴上光束边缘光线的通光直径为：

最大视场斜光束的a光线在棱镜入射面上的通光直径为

　　　　　　D_Ⅰa=KD+2（f₁＇－a－e）tan（－ω_a）

　　　　　　　　=0.5×40+2（161.6－45－43.24）×（－0.00074257）=19.89mm

比较D_Ⅰo和D_Ⅰa，显然棱镜入射面的通光直径应为

D_Ⅰ=D_Ⅰo=21.84mm

（e）确定棱镜的通光直径D_P

由于D_Ⅰ＜D_Ⅱ（前面已取D_Ⅱ=22mm），因此应以棱镜出射面的通光直径D_Ⅱ作为棱镜的通光直径D_P，即取D_P=22mm是合适的，不会造成光束的切割。

（f）根据棱镜的通光直径D_P，查《光学仪器设计手册》上册表5.9，可得到用于本系统中的靴形屋脊棱镜FX_J－90°的全部结构尺寸。

⑦确定h₁、h₂、h₃

给定要求潜望高为：h=250mm，由上述计算可求得物镜到棱镜入射面的距离为

h₂=f₁＇－a－e=161.6－45－43.24=73.36mm

又由手册中查到的结构尺寸可求得棱镜入射面到系统出射光轴间的距离为

h₃=1.945D－0.5D=1.445D=1.445×22=31.79mm

因此可求得反光镜到物镜的距离为

h₁=h－h₂－h₃=250－73.36－31.79=144.85mm

至此，基本完成了八倍炮队镜的外形尺寸计算，现将计算结果整理如下：

物镜：f₁＇=161.6mm，D₁=40mm；

目镜：f₂＇=20.2mm，D₂=25mm；

分划板：D_r=19.77mm；

头部反光镜：40mm×56.57mm；

靴形屋脊棱镜：通光直径D_P=22mm，光程长L=65.56mm；

棱镜的具体结构尺寸见表5.9，这里不一一列出。

反光镜到物镜的距离：h₁=144.85mm；

物镜到棱镜入射面的距离：h₂=73.36mm；

棱镜入射面到系统出射光轴的距离：h₃=31.79mm；

棱镜出射面到分划板面的距离：a=45mm。

应该说明，上述数据尚不是最终的结果数据，在光组具体设计之后尚需作些调整。

2）具有透镜转像系统的望远系统外形尺寸计算

具有透镜转像系统的仪器主要有各种类型的潜望镜以及某些需要长镜筒的瞄准镜。透镜转像系统的基本原理已在10.1节中作了介绍。下面，以应用最多的β_e=－1的双镜组透镜转像系统为例，介绍具有透镜转像系统的望远系统外形尺寸计算方法。⁽¹⁾

（1）给定光学性能与技术要求：

望远系统视放大率Γ=6×；视场2ω=8°；出瞳直径D＇=4mm；镜管长度L=1000mm；入瞳距l_z=－100mm；边缘视场斜光束的渐晕系数K=1/3；要求转像透镜组的通光孔径与物镜的像面直径相等。

（2）拟定光学系统的原理结构图（如图10.24所示）

物镜L₁和目镜L₅构成基本的望远系统，其视放大率Γ₀=－6×；透镜组L₃与L₄构成β_e=－1的透镜转像系统，两透镜组之间为平行光路；为减小后方转像系统的横向尺寸，在物镜的像方焦面上置一场镜L₂；系统L₁、L₂和L₃构成一个望远系统，L₄和L₅构成另一个望远系统。斜光束渐晕系数K值的意义在图中已表示出来。整个望远系统的视放大率应为

Γ=Γ₀·β_e=（－6）×（－1）=6

（3）外形尺寸计算

①计算分配系统各透镜组的焦距

根据给定的要求和几何成像关系，可以确定物镜和其它各透镜组的焦距，如图示应有如下关系：

L=f₁＇+f₃＇+d+f₄＇+f₅＇　　　　　　（10.28）

为求物镜焦距f₁＇，必须首先确定f₃＇、f₄＇、f₅、d和f₁＇的关系。由给定条件，物镜L₁和目镜L₅组成基本的开普勒望远系统，应有：

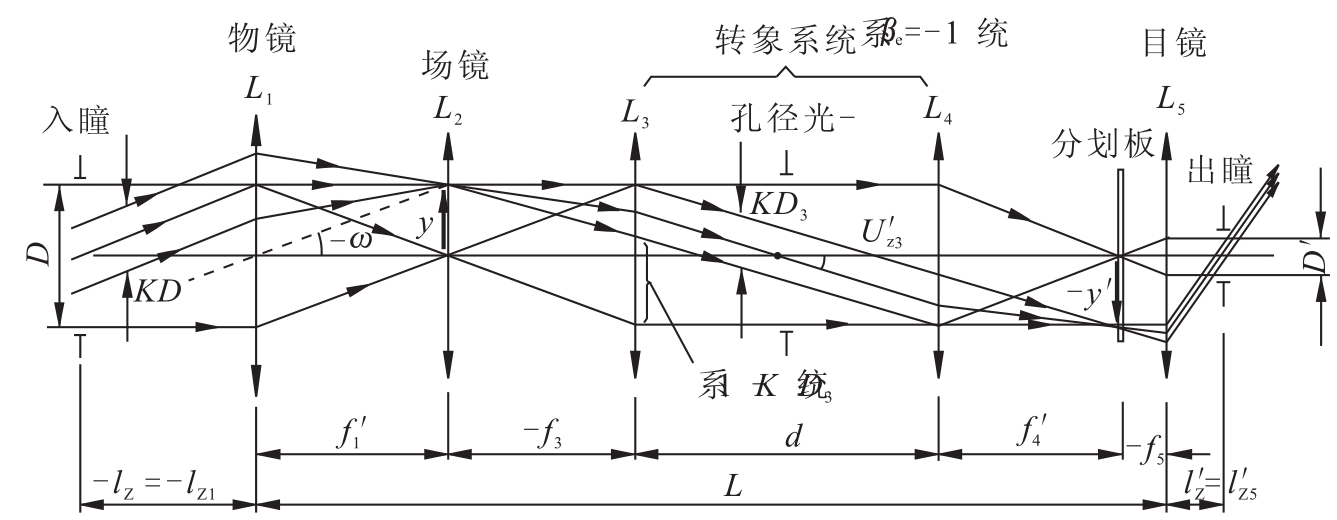
图10.24　透镜转像望远系统光路图

透镜组L₃与L₄构成β_e=－1的双透镜转像系统，考虑到转像系统的成像质量以及场镜和分划板通光口径的匀称性，取转像系统为对称结构，即有f₃＇=f₄＇。

由于透镜组L₁、L₂和L₃构成一个望远系统，故有

由给定的要求，转像透镜组的通光口径与物镜像面的直径相等，即有

D₃=D₂=2f₁＇tanω　　　　　　　　（10.30）

考虑到上述匹配关系，应有

由给定的渐晕条件，以及转像系统的横向放大率β_e=－1，从图中可得到

将Γ₀、式（10.31）、式（10.32）代入式（10.28）中，得到求解f₁＇的方程式：

将下列已知的数据代入上式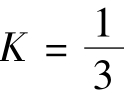：；Γ₀=－6；L=1000mm；tanω=tan4°=0.069927；D=ΓD＇=6×4=24mm。化简后得到：

解出：f₁＇=198.85mm或－259.90mm，因f₁＇＞0，故取f₁＇=198.85mm。

将f₁＇值代入式（10.31），得到

将f₁＇值代入式（10.32），得到

已知Γ₀和f₁＇值，可以得到

将以上计算结果代入式（10.28）验算，有：

L=198.85+230.42+307.22+230.42+33.14=1000.05mm

与给定筒长为1m的要求十分吻合，表明计算正确无误。

②确定场镜焦距

为使光阑在系统中相互衔接，场镜L₂应使物镜的出瞳与转像系统的入瞳重合。由于双透镜转像系统结构完全对称，系统的光阑位于L₃、L₄的中间，其入瞳可由高斯公式求出：

将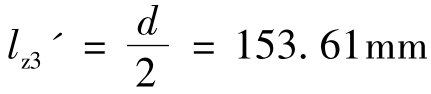和f₃＇=230.42mm代入上式，得到

转像系统的入瞳到场镜的距离为

l_z2＇=f₃+l_z3=230.42+460.81=691.23mm

由于l_z1=－100mm，因而整个系统的入瞳经物镜L₁所成的像其像距为

因而有

l_z2=l_z1＇－f₁＇=－201.16－198.85=－400.01mm

根据上述光瞳衔接的原则，利用高斯公式，可求出场镜的焦距：

③求整个系统的出瞳位置：

根据上述光瞳衔接的原则，转像系统的孔径光阑经透镜组L₄和L₅所成的像即为整个系统的出瞳。利用高斯公式可求出：

l_z5=l_z4＇－（f₄＇+f₅＇）=－460.81－（230.42+33.14）=－724.37mm

上面计算的出瞳距离是合理的，可以满足使用要求。

④求系统各透镜组的横向尺寸

（a）物镜通光直径：由式（10.27）应有

上面的计算结果小于轴上光束的孔径，因而应取

D₁=D=24mm

（b）场镜的通光直径：

D₂=2f₁＇tanω=2×198.85×0.069927=27.81mm

场镜通常采用平凸单透镜，需要时可在平面上刻制分划线，代替分划板。

（c）转像系统的通光直径

D₃=D₄=27.81mm

（d）分划板处视场光阑的直径应为

D_r=D₂=27.81mm

（5）目镜的通光直径

整个系统的外形尺寸计算即告完成。应该再次指出，上述计算过程，是假设各透镜组均为无限薄透镜，按照理想光学系统的解析公式计算的，当光组设计完成后，还会有某些调整。例如，由上面计算出的目镜的通光直径和出瞳位置，都是相对于目镜的主平面而言的，至于目镜组的每个透镜实际要求的通光直径和实际的出瞳距离，只能在目镜的像差设计完成后，根据实际的光路和结构来确定。

【注释】

(1)本例参考文献3的相关内容