轴外点的子午与弧矢光束结构与像差表示

14.1.2　轴外点的子午与弧矢光束结构与像差表示

1）轴外点的子午与弧矢光束结构

当物点位于光轴外时，由物点发出并通过光阑中心到达透镜上P点处的光束中心轴线BP（称为主光线）与光学系统的光轴不在同一直线上，因而整个入射与出射光束将不存在对称轴线，而只存在一个对称截面，轴外点的出射光束结构也将变得复杂，如图14.6所示。为了全面描述轴外斜光束的结构，一般在入射光束中，通过主光线BP取两个互相垂直的截面，其中一个就是斜光束的对称面，即由主光线和光轴决定的平面，称为子午面；另一个是通过主光线并与子午面垂直的截面，称为弧矢面。用这两个截面内的光线经系统折射后出射光线的会聚情况，可近似地反映整个光束的结构和成像质量。当然要更全面地了解光束结构，仅仅了解这两个截面内光线的情况仍是不够的，还须研究截面以外的其他光线。

图14.6　轴外点的子午与弧矢光束结构图（理想情况）

为了表示这两个截面内的光束结构，需要规定若干描述光束结构的几何量，用以度量轴外光束的成像质量，这就是轴外点像差的分类。对于轴外物点的单色像差按性质不同可分成五类，分别是轴外球差、彗差、场曲、像散和畸变；此外，对于复色光成像还有垂轴色差。下面分别进行讨论。

2）轴外点像差的类型、特性与表示方法

根据上述对轴外点成像光束结构的基本分析，轴外点像差按其形成与光束结构的关系，可分为子午光束像差和弧矢光束像差两大类。

（1）子午光束像差

图14.7　子午面内斜光束的光路图

由于系统对子午面对称，因而位于子午面内的光线通过系统后仍位于子午面内。图14.7为子午面内斜光束的光路图。为了描述子午光束的结构，一般研究对称于主光线BP的宽光束成对光线BM⁺和BM^－（称为子午光线对）。若系统没有像差，则所有光线对都应交在理想像点B₀＇上。由于存在像差，BM⁺和BM^－光线对的交点B_T＇（即宽光束的子午像点），可能既不在主光线上，也不在理想像平面上。B_T＇距离理想像平面的轴向距离X_T＇称为子午场曲，而B_T＇距离主光线的垂轴距离K_T＇称为子午彗差。X_T＇、K_T＇这两个量就表示了BM⁺和BM^－这一对子午光线的交点相对于理想像面和主光线的位置偏离。X_T＇和K_T＇的符号规则是：X_T＇—以理想像面为计算起点，到子午光线对的交点，向右为正，向左为负；K_T＇—以主光线为计算起点，到子午光线对交点的垂轴距离，向上为正，向下为负。如果知道了一定数量的子午光线对的X_T＇和K_T＇值，也就可以近似地说明子午光束的结构和成像质量。如果全部子午光束都聚交于理想像面上同一点B₀＇，则所有子午光线对的X_T＇和K_T都等于零。

靠近主光线的细光束，和轴向光束的近轴光线相当，是整个光束的核心部分，它的聚焦情况对整个光束的成像质量有重要作用；而且计算比较简单，不需进行实际光线计算，而只需利用计算主光线所得到的参量，就可以求出当子午光束的宽度趋近于零时B_T＇的极限位置，即细光束的子午像点B_t＇（位于主光线上）。相应的X_T＇的极限值用x_t＇表示，即B_t＇距离理想像面的轴向距离，x_t＇称为细光束子午场曲。

综上所述，子午光束的成像质量，通常用以下三个像差量来表示：

a.x_t＇—细光束子午场曲，它代表理想像面到子午细光束像点的距离，它说明子午细光束在理想像面上的成像质量。

b.δL_T＇=X_T＇－x_t＇—称为子午球差，它代表子午细光束像点B_T＇到宽光束子午光线对交点B_T＇的轴向距离，与轴上点的近轴像点和宽光束与光轴交点的距离相当，称为子午球差。

c.K_T＇—子午彗差，它代表由主光线到子午光线对交点的垂轴距离，因而表示了原来对称于主光线的子午光线对，经过系统以后，其出射光线对主光线失对称的程度。彗差的表观犹如天空中的彗星，因而取名彗差。当主光线高度在上、下光线交点之下时，彗差为正值，即K_T＇＞0，称为过校正。反之，彗差为负值，即K_T＇＜0，此时彗差为欠校正。彗差既是孔径的函数，也是视场的函数。通过对不同的物高追迹上述光线可以求出彗差随视场的变化；通过追迹不同孔径带的光线可以求出彗差随孔径的变化。

总之，根据x_t＇和若干子午光线对的δL_T＇和K_T＇，就可以确定子午光束像的质量，它们统称为轴外点的子午像差。

（2）弧矢光束像差

图14.8中代表光束的弧矢截面。处在主光线两侧与主光线对称的宽光束弧矢光线对BD⁺和BD^－，对称于子午面。由于系统对子午面也是对称的，它们的出射光线也应该和子午面对称，因此出射弧矢光线对必相交于子午面上的同一点B_S＇（称为宽光束弧矢像点）。与子午光线对相似，把理想像面到B_S＇的轴向距离X_S＇称为宽光束弧矢场曲；主光线到B_S＇点的垂轴距离K_S＇称为弧矢彗差。X_S＇和K_S＇的符号规则是：X_S＇—以理想像面为计算起点到弧矢光线对的交点，向右为正，向左为负；K_S＇—以主光线为计算起点到弧矢光线对交点的垂轴距离，向上为正，向下为负。

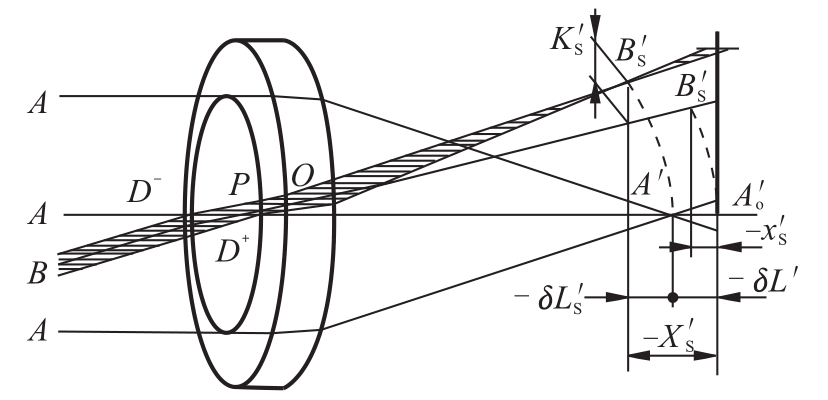
图14.8　弧矢面内斜光束的光路图

主光线周围的细光束的弧矢像点B_S＇与理想像面之间的轴向距离用x_S＇表示，称为细光束弧矢场曲。类似于子午光束，用来表示弧矢光束成像质量的三个像差量是：

a.x_S＇——细光束弧矢场曲。

b.δL_S＇=X_T＇－x_t＇——弧矢细光束像点B_S＇到宽光束弧矢像点B_S＇的轴向距离称为弧矢球差。

c.K_S＇——弧矢彗差。通常，子午彗差为弧矢彗差的3倍，弧矢彗差也可通过追迹空间光线的方法计算出来。

总之，弧矢光束像差的意义和相应的子午像差相似。根据x_S＇和若干弧矢光线对的δL_S＇和K_S＇就可以表示弧矢光束的成像质量，它们统称为轴外点的弧矢像差。

上述这种按其形成与光束结构关系而将轴外点像差划分为两大类的方法，有助于理解各种轴外点像差的本质特点。在此基础上，为了更深入地了解各种轴外点像差的性特点、表示方法与校正方向，将再按轴外点单色像差：慧差、像散、场曲、畸变，以及轴外点的复色光像差（垂轴色差）五类作进一步深入的讨论。

（1）慧差

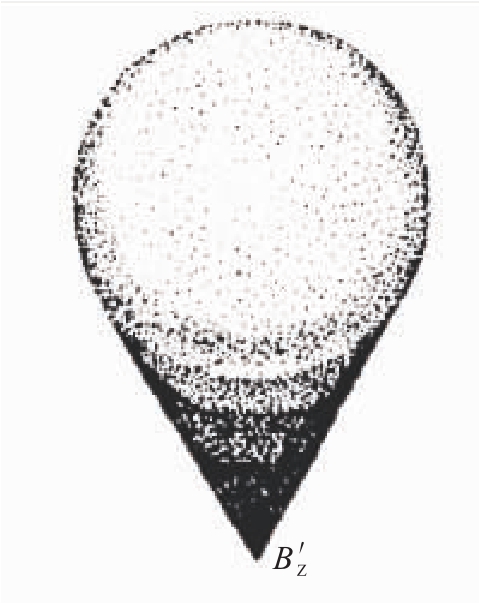
图14.9　彗差——点源成像为彗星形

球差是光学系统孔径的函数，是轴上物点以及轴外物点以宽光束经光学系统成像时均要产生的轴向像差，它的大小和透镜的弯曲有密切关系；与此同时，轴外物点发出宽光束经光学系统成像还将出现另一种像差——彗差。彗差是轴外像差中的一种，它随视场而变化。对于同一视场，由于孔径不同，彗差也不同。因而，彗差是和视场及孔径都有关的一种垂轴像差。彗差使轴外物点的像成一弥散斑，由于折射后的光束失去对称性，所以弥散斑不再对主光线对称，主光线偏到了弥散斑的一侧。图14.9所示为纯彗差时的弥散斑几何图形，在主光线和像面交点B_Z＇处聚集的能量最多，因此最亮，其它处能量逐渐散开，慢慢变暗，所以，整个弥散斑成了一个以主光线和像面交点为顶点的锥形弥散斑，其形状似拖着尾巴的彗星。彗差严重破坏成像清晰度，是一种应引起高度重视的像差。

图14.10表示通过入射光瞳不同位置的光线和这些光线在像面上彗差图中所占有的位置之间的对应关系。图14.10（b）是入射光瞳孔径的正视图。其外圆的光线位置用字母A到H表示，内圆的光线位置用带撇的字母A＇到H＇表示；对应的彗差图样表示在图14.10（c）中，图14.10（b）中的光线在图14.10（c）中的位置用同样的字形标记。从图14.10中可以看出，在系统光瞳孔径上为一个圆环的光线在彗差图上也形成圆环，孔径上小环的初级光线也在像面上形成一个小环，主光线在彗差图上占据顶点P的位置。这样，在孔径上处于不同位置的光线，它们在彗差图形上将处在以P为顶点、夹角为60°的锥体内。因而彗差图可被看作由一系列不同尺寸的圆环组成，像面圆环的尺寸与孔径直径的平方成比例。

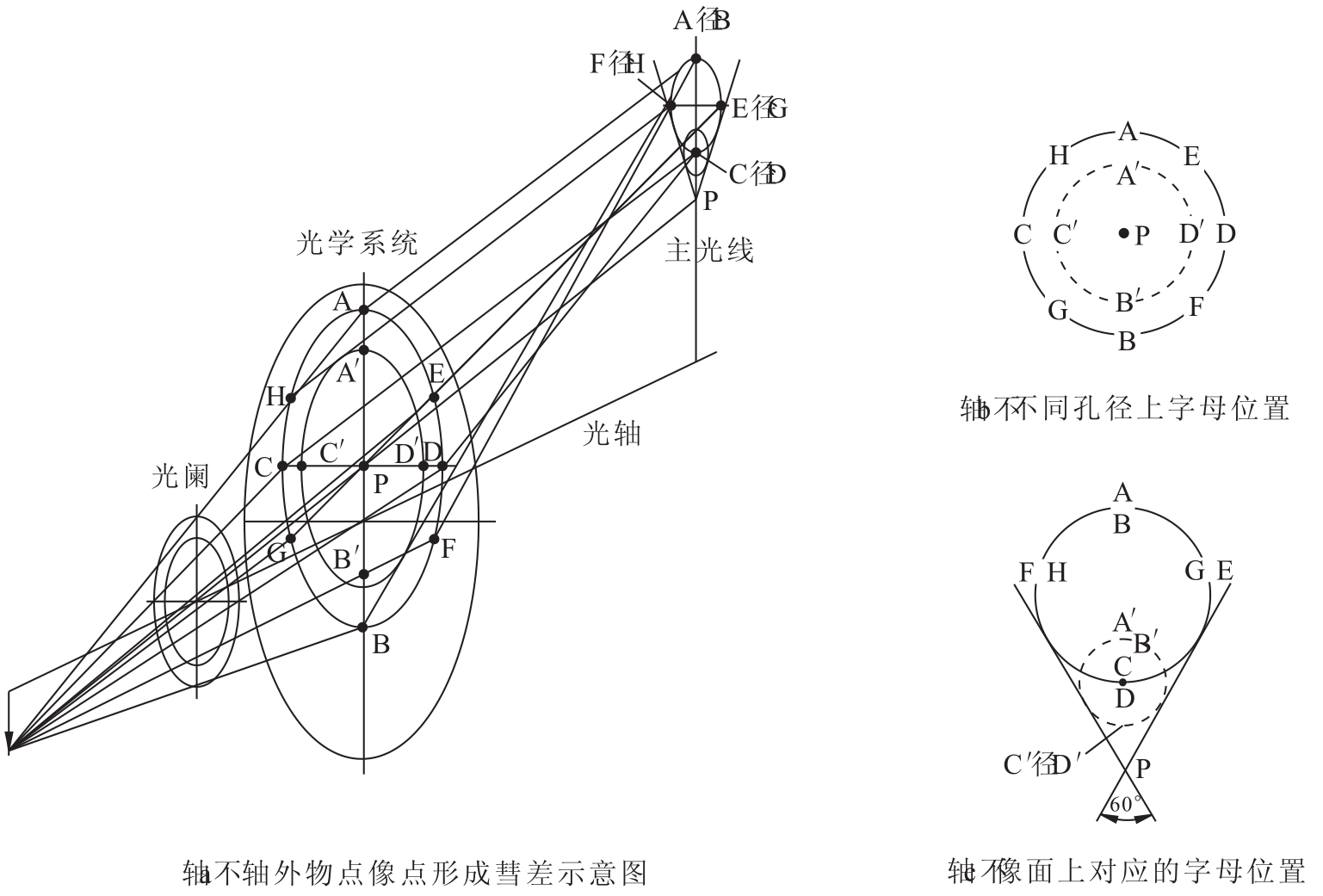
图14.10　通过孔径不同位置处的光线与在彗星图形上成像位置的对应关系

图14.10（c）中，P到AB的距离为子午彗差，P到CD的距离为弧矢彗差。在一般孔径和视场条件下，弧矢彗差近似为子午彗差的1/3；另外，约有一半（55％）以上的能量集中在P和CD间的小三角形区域。因此通常把弧矢彗差作为主要像差有效评价指标之一。

产生慧差的根本原因是由于轴外点发出的宽光束对主光线失对称，即“左右对称，而上下失对称”。因此，在像面上形成的慧差图形也是“左右对称，而上下失对称”由于慧差图形的非对称性，因而在测量中很难确定像点的中心。为此，一个像质优良的光学系统是必须校正彗差的。由于彗差是一种垂轴像差，当物像关系和结构均对称时，彗差可自动消除。

对于某些小视场大孔径的光学系统，由于像高本身较小，彗差的实际数值更小，因此用彗差的绝对数量不能有效地说明系统的彗差特性，一般采用如下的弧矢彗差与像高的比值即正弦差SC＇来反映系统的彗差特性：

正弦差SC＇也是光学系统对正弦条件的偏离程度的描述。当光学系统满足如下条件：

nysinU=n＇y＇sinU＇　　　　　　　　　　　　　　（14.8）

则表示该系统满足正弦条件，满足正弦条件的光学系统即没有正弦差。正弦差实则表示小视场近轴外点的像差和轴上点像差的差别。在小视场的情况下，满足正弦条件即校正了彗差，使近轴外点与轴上点具有相似的成像质量。根据追迹轴上点近轴光线、轴上孔径边缘光线和轴外主光线的结果，即可按公式计算SC＇：

式中：u和u＇分别是近轴光线的物方和像方孔径角，U和U＇分别是边缘光线的物方和像方孔径角，l＇是近轴光线像方交点的距离，L＇是边缘光线像方交点的距离，l_P＇是轴外主光线像方交点的距离（以上l＇、L＇、l_P＇均为相对于系统最后表面的距离）。

（2）像散

对轴外物点发出的斜光束，若把孔径光阑缩至很小，只允许沿主光线的细光束通过光学系统，则系统的子午和弧矢宽光束像差δL_T＇、K_T＇和δL_S＇、K_S＇将基本消失，在理想像面上的成像质量主要由细光束的子午和弧矢场曲x_t＇、x_s＇决定，如图14.11所示。x_t＇和x_s＇之差称为像散x_ts＇，它反映了主光线周围的细光束的成像质量即偏离同心光束的程度。

x_ts＇=x_t＇－x_s＇　　　　　　　　　　　　（14.10）

图14.11中，细的斜光束对称于子午面，由于光束很细，不存在球差和彗差，因而子午细光束经系统折射后必会聚于主光线上子午像点B_t＇，弧矢细光束经系统折射后也必交于主光线上弧矢像点B_s＇。如果光学系统只存在像散，则子午光束和弧矢光束将沿主光线形成两条焦线，分别称为“子午焦线”和“弧矢焦线”。当像平面在子午焦线位置时，得到一条水平焦线；在弧矢焦线位置时，得到一条垂直焦线；在两焦线中间则依次得到椭圆和圆的弥散图形。

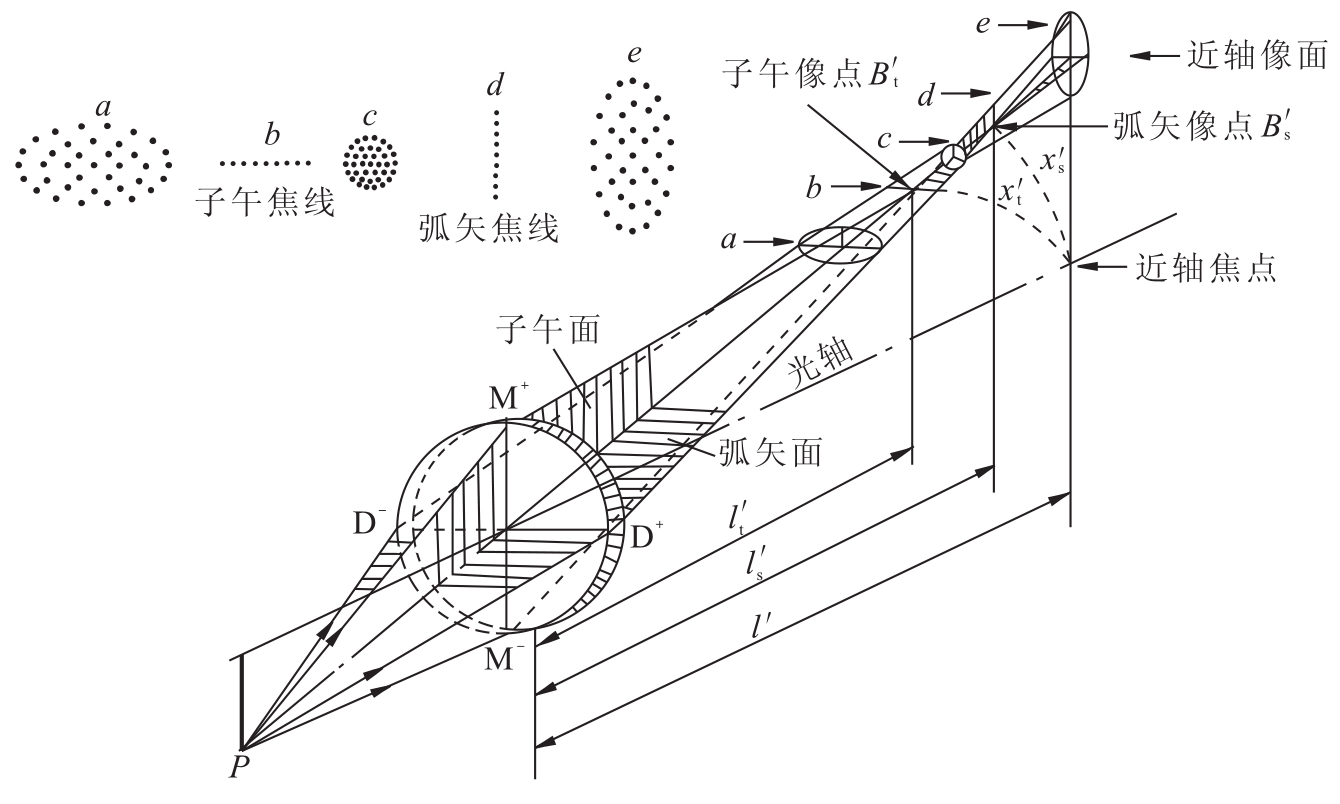
图14.11　细光束场曲与像散

图14.12表示像散随视场的变化。图中横坐标为像散值，纵坐标为像方视场角的正切或像高值。图14.12（a）为欠校正的像散，而且像散为负值；图14.12（b）为像散校正的良好情况，在0.707视场处的像散为零；图14.12（c）为像散过校正的情况，像散为正值。

光学系统的像散是系统中透镜弯曲状态、光阑位置和视场角的函数。其中像散值随视场的变化规律，对初级像散而言，像散是视场平方的函数。一般，对具有较大视场的系统，像差校正均要求校正像散。

（3）场曲

根据高斯光学，垂直于光轴的物平面，经光学系统其理想像应为一垂直于光的像平面。然而，实际光学系统仅在近轴区才满足此性质。对于垂直于光轴的较大的物平面（对应于较大的物方视场）经光学系统成像，当系统不存在其它像差而只存在场曲时，得到的清晰像面将是一个绕光轴回转的弯曲像面（称为匹兹万像面），而非像平面。这种像差现象即为像面（或像场）弯曲，通常简称为场曲。

图14.12　像散曲线

存在场曲时，将影响接收像平面的清晰度，即在接收屏平面上不能得到视场中央与边缘同时清晰的像。移动接收屏或利用测量仪器调焦，当视场中心清晰时，则边缘模糊；反之，视场边缘清晰时，视场中心则又模糊。通常以细光束的交点（或细光束场曲面）相对于理想像面的轴向偏离来表示场曲数量的大小。匹兹万场曲是透镜材料折射率和表面曲率（弯曲）的函数，其量值随视场的增大而增大。

若系统不仅存在场曲而且存在像散时，则如前所述，将存在细光束子午场曲面和细光束弧矢场曲面两个弯曲像面，其场曲量分别以细光束子午场曲（细光束子午交点相对于理想像面的轴向偏离）和细光束弧矢场曲（细光束弧矢交点相对于理想像面的轴向偏离）表征。以符号表示，显然应有

x_t＇=l_t＇－l＇；x_s＇=l_s＇－l＇　　　　　　　　（14.11）

且有细光束像散（见式（14.10））：x_ts＇=x_t＇－x_s＇。

相应地，还存在宽光束子午场曲X_T＇和宽光束弧矢场曲X_S＇，且有

X_T＇=L_T＇－l＇；X_S＇=L_S＇－l＇　　　　　　　　（14.12）

当系统综合存在球差、慧差、像散等像差时，通常以细光束子午焦线和细光束弧矢焦线的中点到理想像面的轴向距离x＇作为系统实际场曲大小的表征，称之为“平均场曲”：

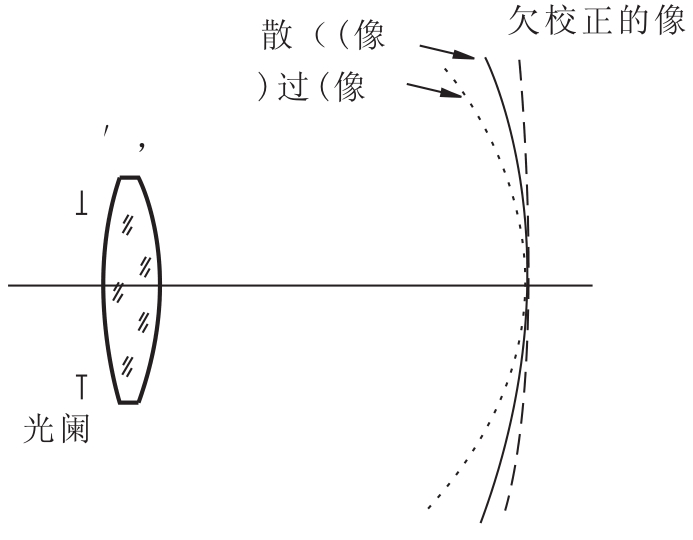
图14.13　单透镜的初级像散

当存在初级像散时，子午像面与匹兹万像面的距离约为弧矢像面与匹兹万像面距离的3倍。由图14.13可以看到：当子午像面和弧矢像面处在匹兹万像面的同一侧，且子午像面处在弧矢像面的左边时，这样的像散是欠校正的，为负值，也叫内向弯曲。当子午像面和弧矢像面左右颠倒时（即弧矢像面在子午像面之左方），像散是过校正的，也叫背向弯曲。通常正透镜使匹兹万像面内向弯曲，负透镜使匹兹万像面背向弯曲。

随着应用场合的不同，对场曲校正的要求也不同。对于目视观察系统，考虑到人眼的调节作用，允许有一定的场曲存在。如目镜，由于视场很大，通常允许有较大的场曲；但对于一些要求接收像面为平面的接收系统如照相物镜、投影物镜以及以CCD作接收元件的摄像物镜等，由于要求轴外点和轴上点的成像质量基本一样，因此对场曲校正的要求就比较严格。

（4）畸变

图14.14　畸变

理想光学系统成像，不仅成像清晰，而且物像相似，即一对共轭物像平面上的垂轴放大率为常数。对于实际光学系统，只有在视场很小的近轴区，才具有物像相似的性质；当视场较大时，像的垂轴放大率就要随视场而异，从而使像相对于物失去相似性。这种破坏物像几何相似使像变形的成像缺陷称作畸变。若以主光线和理想像面的交点B_z＇作为实际像点，用它到理想像点的距离来表示像的变形程度（如图14.14所示），即

δy_z＇=y_z＇－y₀＇　　　　　　　　　　　　（14.14）

式中，y_z＇表示主光线和高斯像面交点高度，y₀＇表示理想像高即高斯像高，用两者之差来表示畸变，称δy_z＇为光学系统的线畸变。

光学设计中通常用相对畸变来表示畸变量。即用某一视场的线畸变δy_z＇与理想像高的百分比表示该视场的相对畸变，以q表示：

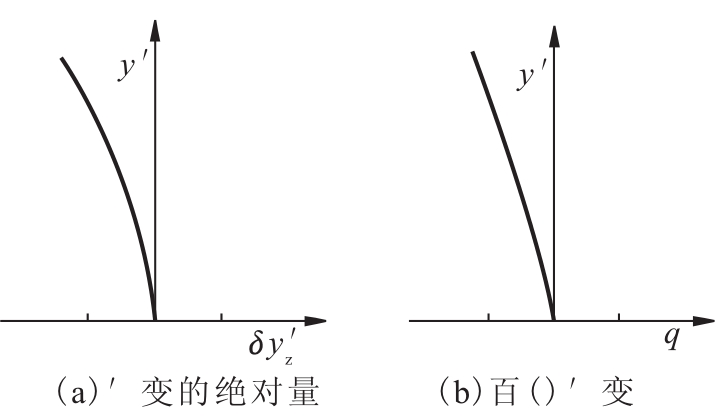
图14.15　畸变曲线

畸变的图示法常用相对畸变随像高的变化来表示，图14.15是典型的畸变曲线。畸变与孔径没有关系，它只是视场的函数。初级畸变随视场（像高）的三次方变化，而相对畸变则随像高平方增加。因而，畸变的变化不是线性的。例如，一个正方形通过光学系统成像将不再是一个正方形。畸变产生的根本原因，是由于光阑在透镜前后的位置变化改变了主光线的折射情况，从而使主光线所决定的像高相对理想像高发生变化，因而破坏物像几何相似性。畸变有两种，以单透镜的成像为例，若光阑在透镜之前，则产生桶形畸变，即视场边缘的像高小于理想像高，畸变为负值，如图14.16（a）所示；若光阑在透镜之后，则产生枕形畸变，即视场边缘的像高大于理想像高，畸变为正值，如图14.16（b）所示。

图14.16　畸变的分类

畸变也是一种垂轴像差，但它只引起像的变形，而对像的清晰度并无影响。因此，对于一般的光学系统，只要接收器感觉不出所成像的变形，这种畸变像差就无大碍。如在目视仪器中，畸变可允许到4％。但对某些要利用像来测定物体的大小和轮廓的光学系统，如计量仪器中的投影物镜、工具显微镜以及航空测量用的摄影物镜等，因畸变直接影响测量精度，畸变应为重点校正的像差，予以严格校正。如计量仪器物镜畸变一般要求小于万分之几。

（5）垂轴色差

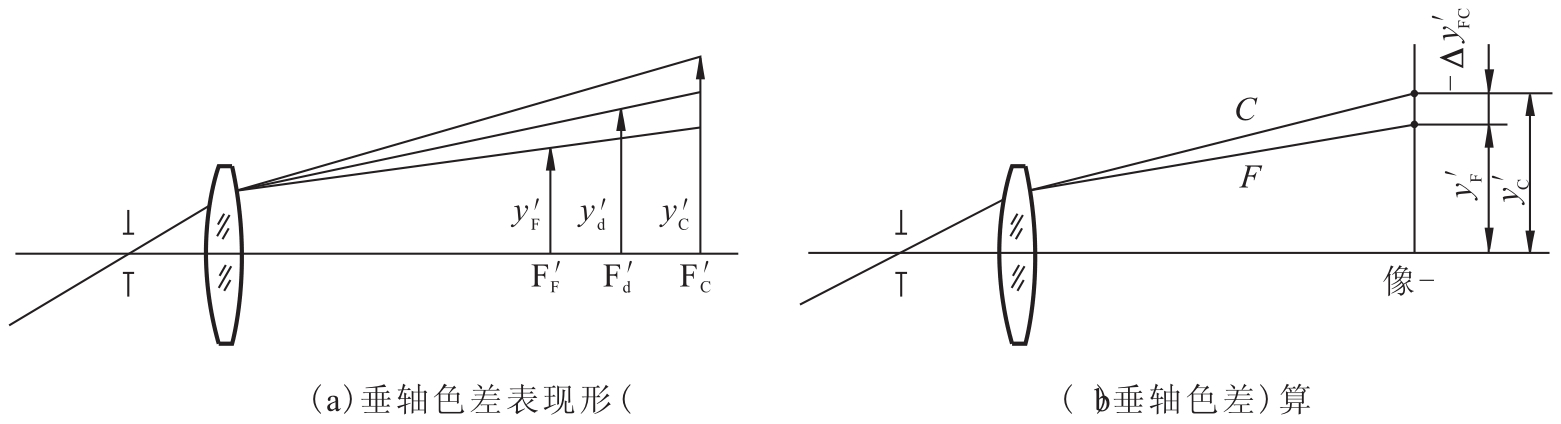
图14.17　垂轴色差

代表一定物高（视场）的轴外复色光（如白光）物点成像时，由于透镜的折射率及相应的焦距值随光线波长的变化而变化，因而除产生轴向位置色差外，还将使光学系统的放大率随光线波长变化而变化，最终表现为不同色光物点的像高各不相同。如图14.17（a）所示，无限远轴外白光物点通过单透镜成像后，红光（C）的像高最大，紫光（F）的像高最小，这种不同颜色光线像高的差异称为垂轴色差，或倍率色差。当光学系统存在垂轴色差时，轴外物体所成的像将出现由红到紫的色边，因而像也将是模糊的。垂轴色差一般用两种指定波长光线（如F、C光）在理想像平面上主光线的投射点高度之差Δy_FC＇表示，如图14.17（b）所示。

Δy_FC＇=y_F＇－y_C＇　　　　　　　　　　　　（14.16）

轴上点显然没有垂轴色差，不同像高的像点垂轴色差各不相同，一般随着像高（视场）的增加而加大；另外，垂轴色差与光阑位置有关，光阑在透镜前和透镜后Δy_FC＇的符号相反。用不同色散的光学玻璃做成的正透镜和负透镜组合在一起，可以消除色差。所以实际光学系统中的透镜组大多数由正透镜和负透镜组合而成；通常也是对0.707视场校正垂轴色差。

如图14.17所示，存在色差的光学系统将使像点不再是一个白色的光点，而成为一个彩色的弥散斑。对于轴上像点，这个弥散斑的彩色分布是中心对称的；对于轴外像点，彩色沿单方向分布，即像点在一个方向上呈现彩色。总之，无论是位置色差还是垂轴色差，都将直接影响像的清晰度，并破坏像相对物在色彩上的相似性。所以，对于像质和色彩还原性要求高的成像系统，必须严格校正色差。