光学自动设计基本原理

15.1.1　光学自动设计基本原理

光学自动设计是计算机技术和最优化数学方法在光学领域最早最成功的应用之一。由于光学设计问题的复杂性和庞大的计算量，计算机技术的发展不仅使光学设计工作者从繁重的计算工作中解放出来，而且给光学设计带来了新的活力。计算机技术在光学设计中的应用经历了3个不同的阶段：第一阶段只是简单地代替人工计算像差；第二阶段是由计算像差进一步计算像差变化量表，作为分析和校正像差的依据；第三阶段是在像差变化量表的基础上，求解结构参数，自动修改结构，校正像差，即所谓的自动设计或像差自动校正。

光学自动设计所要解决的核心问题是像差设计问题，即根据初始设计给出的对系统中每个透镜组的光学特性和成像质量的要求，计算机按照一定的程序自动地寻找并确定像差最小、像质最佳的透镜组结构参数，包括所用的玻璃材料、每个球面的曲率半径和它们之间的厚度、间隔等。如果系统中采用了非球面，还要给出它们的非球面系数。

在光学自动设计数学建模过程中，为了讨论方便是，通常将光学系统的结构参数，包括各面曲率半径、间隔、厚度及折射率等，统一记作x=（x₁，x₂，…，x_N）。随光学系统结构参数改变的参数，如光学特性参数（包括焦距、放大率、物距、像距、入瞳位置、出瞳距离等）以及代表成像质量的各种几何像差或波像差等参数，统称为像差，记作F=（F₁，F₂，…，F_M）。改变结构参数，系统的各种像差随之改变，即像差是结构参数x的函数，两者之间的函数关系可用下列方程组表示。

　　　　　　　　　　F₁=f₁（x）=f₁（x₁，x₂，…，x_N）

　　　　　　　　　　F₂=f₂（x）=f₂（x₁，x₂，…，x_N）

　　　　　　　　　　……

　　　　　　　　　　F_M=f_M（x）=f_M（x₁，x₂，…，x_N）

或写成

F_i=f_i（x）=f_i（x₁，x₂，…，x_N）　　　　　i=1，2，…，M　　　　　（15.1）

式中，f_i分别代表像差F与光学结构参数x之间的函数关系。式（15.1）是一个十分复杂的非线性方程组，称为像差方程组。

光学设计问题从数学角度来看，就是建立和求解像差方程组。即根据系统要求的像差值，从上述方程组中直接求解出所要求光学结构参数x。这一直是光学设计领域人们长期追求的目标。但是，由于问题本身的复杂性，到目前为止还不能够找出方程组具体形式的函数关系，更不可能求解；然而，反过来只要给出了具体的结构参数x，却可以依靠光路追迹计算和像差理论知识，用数值计算方法计算出函数值F的。事实上，在没有使用计算机以前，传统的光学设计方法是首先选定一个全部结构参数已确定的初始系统作为设计出发点，设计者依靠设计经验和像差理论知识，一边对系统的部分结构参数进行修改，一边计算像差值，反复这个过程，直到所有像差值符合要求为止。这一过程的计算工作量非常大，人们只能依靠经验，逐步修改，反复计算，因此设计一个光学系统往往是一个冗长繁重的计算过程。

随着计算机的出现及其在光学设计中的迅速应用，目前计算工作量已经不再是光学设计的主要矛盾。主要问题又重新回到寻找像差和结构参数之间的解析表达式，以便直接求解结构参数。但因为像差和结构参数之间的函数解析关系还无法找到，因而工程数学中常采取一种方法是把函数关系f_i用系统的结构参数x的幂级数展开表示，然后用数值计算的方法，求出函数值F对每个结构参数x₁，x₂，…，x_N的差商，并用它近似代替微商，作为幂级数的系数。这样，函数值F表示成结构参数x的幂级数形式就可确定。目前常用的方法还限于计算它们的一阶偏微商，把f_i表示成结构参数的幂级数一次项展开形式，把像差和结构参数之间的函数关系近似用线性函数代替。即在初始结构参数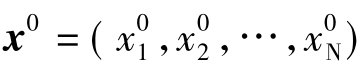附近对像差f_i（x）按泰勒级数展开，并只取到线性项：

式中：——初始结构参数；

　　　x_j——迭代后系统的结构参数，j=1，2，…，N；

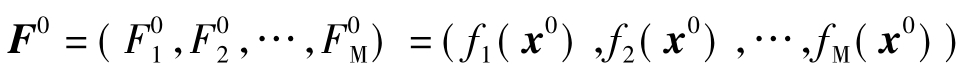　　　——初始系统的像差值；

微商af_i（x⁰）/ax_j——第i种像差对于第j个初始结构参数的变化率，i=1，2，…，M，j= 1，2，…，N；上式的意义是当各结构参数由初始值x⁰改变到x时像差由F⁰变到F。将af_i（x⁰）/ax_j记为a_ij，x_j－x⁰_j记为Δx_j，则式（15.2）中的各种像差可写成

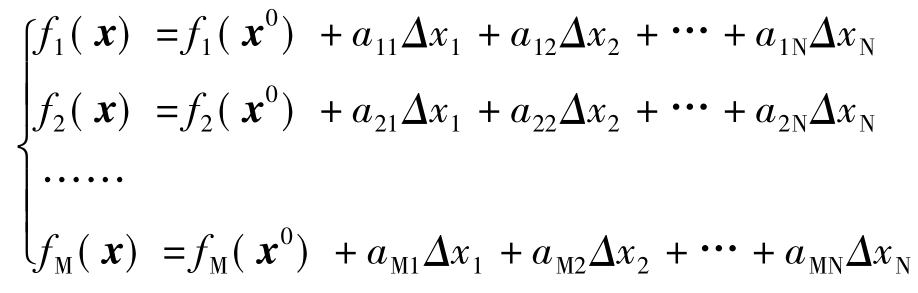
或写成矩阵形式

F=F⁰+AΔx　或　AΔx=ΔF　　　　　　　　　　　　（15.3）

该式称为像差线性方程组，其中

光学系统设计时，首先，给出初始系统的结构参数x⁰，计算出其各种像差值F⁰，然后依次给每个自变量增加一个小量δx_j，重新计算出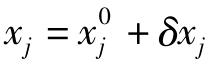对应的像差F和像差增量ΔF= F－F⁰=（δF₁，δF₂，…，δF_M）^T，并求出差商δF_i/δx_j，当δx_j取足够小时，用差商δF_i/δx_j代替微商af_i（x⁰）/ax_j，作为式（15.3）的系数矩阵A。然后，根据光学系统要求的像差目标值F，求解线性方程组得Δx。由于Δx是非线性方程的近似解，所以，用Δx_p=pΔx对原系统结构参数进行修改，p为一个小于1的常数，得新系统结构参数x=x⁰+Δx_p。当p足够小时，上述过程总可以获得一个比原系统像质有所改善的新系统。在此基础上重复上述过程，重新建立像差线性方程组并进行求解，直到各种像差满足要求为止。这种像差校正过程实质上是用线性方程组来近似代替非线性方程组，然后逐次逼近求解非线性方程的解，即数学上的牛顿法求解非线性方程组。这是目前绝大多数光学自动设计程序采用的主要数学过程。

牛顿法求解非线性方程的解所用线性近似方法只能在原始系统周围较小的自变量空间才有意义，因此必须用逐次逼近的办法使光学系统像质逐步改善。另外使用这种方法还必须给定一个原始系统结构参数x⁰，然后再以x⁰为原始出发点，进行求解。这样做实际上只能在原始系统的附近找出较好的解。这个解不一定能满足要求，而且很有可能不是系统的最好的解。目前各种光学自动设计方法只是求解像差方程组的方法以及限制解向量x大小的方法不同而已，它们的基本出发点都是相同的。正因为如此光学自动设计并不是万能的，有它本身的缺陷和局限性。但它与人工修正结构参数相比较，已经前进了一大步。

求解像差线性方程组式（15.3）似乎是一个简单的数学问题，然而实际上并不简单。首先该方程组中方程式个数（像差数）M和自变量的个数（可变的结构参数个数）N并不定相等，有可能M＞N或M≤N；另外系统的像差并不一定能全部校正。求解像差方程组就成了优化数学的问题。求解方法不同对应着不同的算法和程序，目前得到广泛应用的主要有阻尼最小二乘法、正交化法和适应法。这里主要介绍阻尼最小二乘法求解线性方程组的方法。