奇偶数趣谈
你知道,能被2整除的数叫做偶数;不能被2整除的数叫做奇数。你可注意到奇数与偶数有一个显著的特点:就是它们的相间性,即一个奇数后面是一个偶数;一个偶数后面是一个奇数。利用奇偶数的这一特征,和下面一些显而易见的运算性质:奇数土奇数;偶数偶数±偶数=偶数 偶数±奇数=奇数 奇数X奇数=奇数 偶数X偶数=偶数 奇数X偶数=偶数,我们可以解决很多用其他方法不好解决的问题。如:“7只茶杯口朝上放在桌上,每回翻转其中的4只,能不能做到使7只茶杯全部变成口朝下?”
如果当真去试验一下的话,情况将会很复杂,因为每回究竟翻转哪4只有许多不同的选择,于是,我们把思路集中到1只茶杯上,容易想到,一只茶杯无论翻多少次,只要翻转的次数是偶数,杯口的方向一定会保持原样;只有当翻转的次数是奇数时,杯口的方向才会向下。所以7只杯口要从向上变为向下,翻转的总次数一定是7个奇数的和,仍然是一个奇数。而每回翻转4只相当于1只1只地翻转4次,无论翻转多少回;总次数都是偶数,即4的倍数,因此,所提要求是无法实现的。
从上面题目得到一个经验:当一件事物只有两种状态时,如上与下,正与反,开与关,通与断……就可以联系奇偶数来考虑。
有时还可以采取形象化的处理方法。在中国象棋盘上,马跳奇数次能不能回到原来的位置?
这里用:试验的方法是不行的。因为我们不能断言要试多少次才能发生这种情况。为此,我们用黑白相间的两种颜色把棋盘上的点分成黑点白点两类,正如整数分成奇、偶数一样。现在我们可以知道,马在原来的位置无论向什么方向每跳一步,点的颜色就会随着改变一次。因此,马跳了奇数次后,颜色必然与原来不同,更谈不上跳回原位了。
再看一个例子:“在一张纸上画了34个方格(如图1),能不能用一些两个方格连在一起的小纸片,把这34个方格全部盖住而没有重叠?”

图1

图2
这道题如果简单地根据34能被2整除就做出肯定的回答是没有说服力的,因为没有考虑小纸片的排法。那么能不能用试验的方法来解决呢?这里我们采取染色的方法(如图2),可见,图中有16个黑格子,18个白格子,小纸片无论怎样放,盖住的格子总是一黑一白,所以无论每样排都会剩下两个白格盖不上。
上面两题所使用的方法叫“染色法”,是对奇偶相间性的巧妙应用。
最后请看一道有趣的题:
有一只奇怪的猫不仅非常善于捕鼠,而且吃老鼠的方式也很独特。每天晚上它总是让捕到的老鼠站成一行从1开始编号,然后把编号是奇数的吃掉,再让剩下的老鼠原地不动重新从2开始编号,再把编号是奇数的吃掉……照此方法直到吃到剩下一只为止,让这只老鼠留下来。可有一天,这只猫忽然发现有一只小白鼠一直留了下来。那么这只聪明的小白鼠是采用了什么方法躲过了一关又一关呢?
我们假定小猫一天捕10只老鼠,从下图可以看出,8号老鼠在前3轮编号一直处于偶数位置。
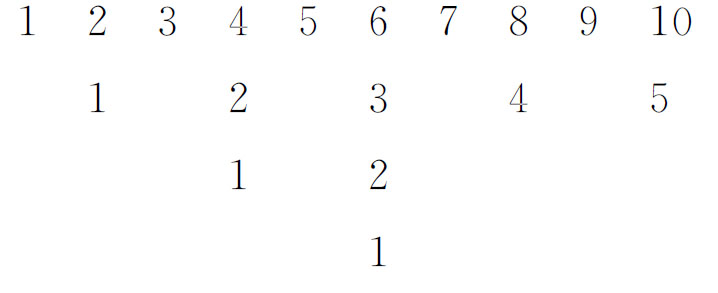
从上面过程可以想到,因为每一轮总是把偶数号的老鼠留下来,所以谁编号中含有因数2越多,谁留下的机会就越多。聪明的小白鼠采取的策略是:先数一下是多少只老鼠,然后找出这个范围内含因数2最多的数是几,当它看到老鼠的总数刚刚大于其中某个数时,就抢先站在这个编号的位置上,于是它就能成为唯一的幸存者。
(彭景康)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














