离散型随机变量

若随机变量的取值为有限个或可列个，则称此随机变量为离散型（discrete）随机变量，简称离散量。

例如，§2.1中的例2.1.1与例2.1.2中的随机变量取值均为有限个，故它们均为离散型随机变量。又如，抛一枚硬币，直到正面首次出现所需的抛掷次数，一个广场上的人数等等，这些量可能没有上限，但均可列，所以这些量也是离散型随机变量。若以X记某一地区成年男子的身高，以Y记某产品的寿命，显然X与Y的取值充满着某一区间，它们的可能取值不能一一列出，所以X与Y不是离散量。

离散量的统计规律通常用概率分布律来描述。

设X为离散量，若其可能取值为，则称

为X的概率分布律（distribution sequence）。

概率分布律也可用下面的列表方式来表示：

概率分布律有以下两条性质：。

性质（1）是显然的。性质（2）是因为是不同的样本点，即对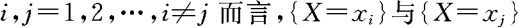是两两不相容的，这样就得到了性质（2）。

例2.2.1　随机变量X的概率分布律为

求常数c的值。

解　这里先回忆一下高等数学中的一个函数展开式。由概率分布律的性质知，

那么。

以下介绍几个重要的离散量。

（一）0-1（p）分布

若随机变量X的概率分布律为

其中，0＜p＜1、则称X为服从参数为p的0-1分布，也称为两点分布。并用记号X～0-1（p）表示（也可表示为B（1，p））。

例如：若某一地区每一个新生儿是男（或女）的概率为。0.51（或0.49），记｛X＝1}为男孩，{X＝0}为女孩，则X～0-1（0.51）。

（二）二项分布

若随机变量X的概率分布律为

其中，，则称X服从参数为（n，p）的二项（binomial）分布，且记为。

显然，（2.2.2）式中，且

在讨论二项分布时必须提到下面的重要试验。

定义2.2.1　在n次独立重复的试验中，每次试验都只有两个结果：，且每次试验中A发生的概率不变，记，称这一系列试验为n重贝努里（Bernoulli）试验。

例如，若考虑一个试验的结果只有成功与失败，且每次成功的概率都为p，O＜p＜1，这样独立重复地进行的n次试验即为n重贝努里试验．又如，独立重复地抛n次硬币，每次结果只有正面或反面；在一放有红球与其他颜色的球的袋中有放回地摸球n次，每次只记录摸到红球与其他球（非红球）两种结果，且设每次摸到红球的概率是p，O＜p＜1，等等，都可以看成是n重贝努里试验。

在n重贝努里试验中，若记事件A发生的概率为P（A）＝p，O＜p＜1。设X为在n次试验中A发生的次数，则X～B（n，p），即

因为事件｛X＝k｝即为“在n次试验中恰有k次A发生且有。n-k次A不发生”，这k次可以是n次中的任意k次，故有种方式，而每一“特定的k次A发生且特定的（n-k）次A不发生”的概率为，这样就得到了（2.2.2）式。读者可以再详细地看一下§2.1例2.1.1中随机变量X的概率分布律的求解过程。特别地，当n＝1时，B（1，p）即为。0-1（p）分布。

例2.2.2　由6位品酒师独立投票评定某种酒是否为优质酒，若6位中有4位投票同意，则定该酒为优质酒，且设每位品酒师作出正确判断的概率为p，0＜p＜l。求：

（1）若该酒为优质酒时，能作出正确判断的概率α。（2）若该酒不为优质酒时，能作出正确判断的概率β。

解（1）当该酒为优质酒时，至少要有4位品酒师作出正确判断才能判定此酒为优质酒，所以

（2）当该酒不是优质酒时，则至少要有3位品酒师作出正确判断，所以

例2.2.3　设有一大批优质品率为p的产品，O＜p＜1，用以下方式进行验收：第一次先从中随机取5件，若至少有4件是优质品则接收该批产品，若优质品不到3件就拒收；否则再第二次从中抽2件，若2件均为优质品就接收，否则就拒收。求：（1）第一次抽样就接收该批的概率α。（2）该批产品被接收的概率β。

解　由题意知，各次抽样结果相互独立（由于是一大批，总的数自很多）。设X为第一次抽到的优质品数，Y为第二次抽到的优质品数，显然。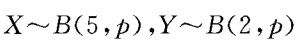

一般情形下，当n不是很大的时候，对于二项分布的计算还是比较容易的，但当n比较大的时候，二项分布的概率值可以采用Excel计算。

例2.2.4　假设，现分别计算P（X≤10）和P（X＝10）。

解　先计算P（X≤10），由二项分布可知：

显然这个计算不是很简单，但可以通过Excel表单简单得出。具体如下：在Excel表单的任一单元格输入在主菜单中点击“插入”“函数（F）”在选择类别的下拉式菜单中选择“统计”选择“BINOMDIST”点击”确定” 在函数参数表单中输入“Number_s＝10，Trial＝100，Probability_s＝0.05，Cumulative＝TRUE”，然后点“确定”即在单元格中出现“0.98852759”。

如果要计算P（X＝10），则只需要在上面的过程中所有的步骤中把“Cumulative＝TRUE”改“Cumulative＝FALSE”。即在单元格中出现“0.016715884”。

（三）泊松分布

若随机变量X的概率分布律为

其中λ＞0，则称X服从参数为λ的泊松（Poisson）分布，且记为。

观察（2.2.3），显然有对任意的，且由§2.2的例2.2.1知，。

参数λ的含义将在第四章中说明，而有关泊松分布的数学模型将在随机过程第十二章中研究。

泊松分布有着非常广泛的应用．这是因为当n足够大，p充分小（一般要求p＜0.1），且np保持适当大小时，参数为（n，p）的二项分布可用泊松分布近似描述。

设X～B（n，p），并记λ＝np。则

当n充分大和适当的λ时，

也就是说，当n充分大，p足够小时，

根据统计工作者的经验，以下的随机变量常可近似用泊松分布描述：

1．某产品的不合格点数；

2．一本书一页上的印刷错误数；

3．一手机某一时间段内收到的信息次数；

4．某放射物在一定时间内放射出的α粒子数；

5．一定的时间区间内进入某书亭的人数。

例2.2.5　设某公共汽车站单位时间内候车人数X服从参数为4.8的泊松分布。求；（1）随机观察1单位时间，至少有3个人候车的概率；（2）随机地独立观察5个单位时间，恰有4个单位时间至少有3人候车的概率。

解　（1）由题意知，X～π（λ），其中λ＝4.8则

（2）设被观察的5个单位时间内有Y个单位时间是“至少有3个人候车”，则Y～B（5，p），其中p＝P｛X,≥3｝＝0.8575。那么

例2.2.6　某地区一个月内每200个成年人中有1个会患上某种疾病，设各人是否患病相互独立。若该地区一社区有1000个成年人，求某月内该社区至少有3人患病的概率。

解　记p＝1/200，且设该社区1000人中有X人患病。由题意知，X～B（1000，p），记λ＝1000p＝5。利用（2.2.4）式，所要求的概率为

例2.2.7　例2.2.6的计算可以通过Excel表单简单得出。先计算出P｛X≤2｝具体如下：在Excel表单的任一单元格输人“＝”在主菜单中点击“插入”“函数（F）”在选择类别的下拉式菜单中选择“统计”选择“POISSON”点击“确定”在函数参数表单中输人“X＝2，Mean＝5，Cumulative＝TRUE”，然后点“确定”即在单元格中出现“0.124652019”。P｛X≥3｝＝1－P｛X≤2｝＝0.875347981。

（四）其他离散型随机变量

例2.2.8　一袋中共有N个球，其中有a个白球与b个红球（a＋b＝N）。从中不放回地取n（n≤N）个球，设每次取到各球的概率相等。若其中有X只白球，试写出X的概率分布律。

解　这是一个等可能概型，

其中。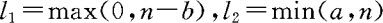

如果随机变量X具有形如（2.2.5）的概率分布律，则称X服从超几何（hypergeometric）分布。

例2.2.9　设独立重复试验中，每次试验有两个结果：。每次试验中A出现的概率不变，记P（A）＝p，0＜p＜1，设直至A首次发生时所需的试验次数为X，求X的概率分布律。

解　参照§2.1的例2.1.1中求Y的概率分布律的方法，可知

如果随机变量X具有形如（2.2.6）的概率分布律，则称X服从参数为p的几何（geometric）分布。