随机变量函数的分布

在实际问题中，我们常会碰到已知一随机变量的分布，要求这一变量的函数的分布问题。例如，已知到达车站的时间服从某一区间上的均勾分布，要求候车时间的分布；已知半径测量值为正态分布，要求对应的圆面积的分布，等等。本节要研究一个随机变量函数的分布问题。即已知X的分布，Y＝g（X），要求Y的分布。下面先来看几个例题。

例2.5.1　抛一枚骰子，当点数不大于3时定义Y＝－1，当点数为4或5时定义Y＝0，当点数为6时定义Y＝l。且记Z＝Y2。（1）求Y的概率分布律；（2）求Z的概率分布律。

解　（1）设抛一枚骰子得到的点数为X。由题意知当且仅当｛X≤3｝发生时｛Y＝－1｝发生，我们称事件｛X≤3｝与事件｛Y＝－1｝等价。同理事件｛X＝4｝∪｛X＝5｝与｛Y＝0｝等价，事件｛X＝6｝与｛Y＝l）等价。故有

即

（2）由题意知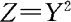的可能取值为0，1。与（1）的解法相同，得

例2.5.2　设一商店某一批电子产品使用寿命（以小时计）X～E（λ），λ＝l/250。商店对该批产品实行先使用后付款的办法销售。若使用寿命小于100小时，顾客不用付费；若使用寿命大于100且小于250小时，顾客得付10元；若使用寿命大于250小时，则要付30元。求顾客付费的概率分布律。

解　设顾客付费的金额为Y元，Y的可能取值为：0，10，30。由题意知X～E（λ），λ＝1/250。由于电子产品使用寿命小于100小时，顾客不用付费，那么

同理可得

由例2.5.1，例2.5.2可知，若X的分布已知，Y＝g（X），且Y为离散量时，可先列出Y的可能取值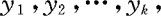…然后找出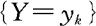事件的等价事件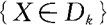，从而求出Y的分布律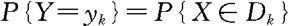即可。另外，当Y＝g（X）为连续量时，我们总是先找出｛Y≤y｝，即｛g（X）≤y｝的等价事件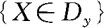，从而求出Y的分布函数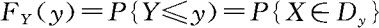。总之，求随机变量函数的分布问题实质上就是找等价事件问题。

例2.5.3　设随机变量X的概率密度为

Y＝X2，求Y的概率分布函数及密度函数。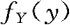

解　由题意知，当i≤0时，。

当0＜y＜9时，{Y≤y｝的等价事件为。所以

例2.5.4　设X的概率密度为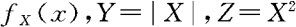。求Y与Z的概率密度。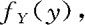

解　设Y与Z的分布函数分别为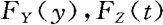。当y≤0时，显然有。当y＞0时，有

当t≤0时，显然有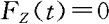。当t＞0时，有

定理2.5.1　设X为一连续型随机变量，其概率密度为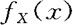，随机变量Y＝g（X），若函数y＝g（x）为一严格单调增函数（或减函数），且可微。记y＝g（x）的反函数为x＝h（y）。则Y的概率密度为

其中D为函数y＝g（x）的值域。

证明　先设y＝g（x）为一严格单调增函数，即g′（x）≥0，注意此时的h′（y）≥0。而Y的分布函数为

从而。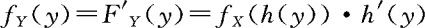

若y＝g（x）为一严格单调减函数，即g′（x）≤0，此时并有h′（y）≤0。故Y的分布函数为

从而。这样就证明了（2.5.1）式。

例2.5.5　随机变量求Y的概率密度。

解　记y＝g（x）＝ax＋b，则其反函数为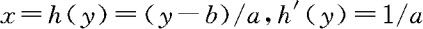。满足定理2.5.1的条件，故有

即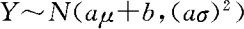。特别地当。

也就是说一个正态量的线性函数仍为正态量；特别地，当是标准正态量。

例2.5.6　设连续型随机变量X的分布函数为F（x），且当0＜F（x）＜1时F（x）为严格单调函数，记Y＝F（X），证明：Y服从区间（0，1）上的均匀分布。

证明　由分布函数的性质知，0≤F（x）≤l，故Y的取值也属于区间［0，1］。显然有，当y≤0时，。

当0＜y＜1时，

因为X的分布函数为F（x），故有

即

由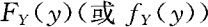的表示式就知Y～U（0，1），命题得证。