二元随机变量的分布函数

在§3.1中我们研究了二元离散型随机变量的联合分布律，边际分布律与条件分布律。对二元随机变量的分布函数，我们同样要研究这三方面的内容。

（一）二元随机变量的联合分布函数

定义3.2.1　设二元随机变量（X，Y），对于任意的实数x，y，称函数

图3.2.1

为（X，Y）的联合分布函数。

若将（x，y）看作随机点的坐标，则分布函数F（x，y）即为（x，y）落在图3.2.1阴影部分区域的概率。

与一元随机变量的分布函数一样，相应地，F（x，y）具有以下性质：

（1）当给定关于y单调不减；当给定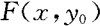关于x单调不减。

（2）。

（3）关于x右连续，关于y右连续。（证略）

（4）当实数时，

性质（1），（2）可参照一元变量的分布函数相应性质的证明方法进行证明。

为了证明性质（4），设。易知。从而

（二）二元随机变量的边际（边缘）分布函数

在§3.1中我们称单个变量的概率分布律为边际分布律，在此我们同样称单个随机变量的分布函数为边际分布函数。

记二元变量（X，Y）的联合分布函数为F（x，y），X，Y的边际分布函数为，则

同理，。即，二元随机变量的边际分布函数是联合分布函数当另一个变量趋向于＋∞时的极限函数。

以后我们不一一说明地常用表示X，Y的边际分布函数，用F（x，y）表示（X，Y）的联合分布函数。

（三）条件分布函数

设（x，y）为二元离散量，当时，称函数

为条件下Y的条件分布函数。

设（X，Y）为二元连续量（下一节介绍），当任意固定时，称函数

为｛X＝x｝条件下Y的条件分布函数。

条件分布函数具有分布函数的所有性质。

例3.2.1　一袋中有a个白球，b个红球，记a＋b＝n。每次从袋中任取一球，不放回抽样，设

（1）试写出的联合分布函数的边际分布函数写出当的条件分布函数。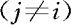

解　记。由第一章的例1.3.2，可知。

当，因此

于是可得的联合分布律如下：（记N＝n（n－1））

那么的联合分布函数F（x，y）为

（2）有两种求法。方法一，由的边际分布律求；方法二，可由。现采用方法二。

（3）由的联合分布律可知，在的条件下，的条件分布律为

所以所要求的条件分布函数为