二元连续型随机变量

（一）二元连续量的联合分布

定义3.3.1　设（X，Y）为二元随机变量，若存在二元函数f（x，y）≥0，对任意的二维空间的集合D，有

则称（X，Y）为二元连续型随机变量，简称二元连续量。称f（x，y）为（X，Y）的联合概率密度，简称联合密度。

f（x，y）具有以下性质：（其中F（x，y）为（X，Y）的联合分布函数）

（4）在f（x，y）的连续点上有

由连续量的定义可知，二元连续量（X，Y）落在一面积测度为零的区域上的概率为零，特别地落在一条曲线上的概率为零。

由f（x，y）的性质（4）知，在f（x，y）的连续点处有

这表明（X，Y）的联合密度为（X，Y）落入矩形区域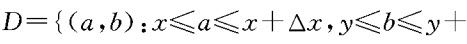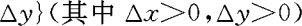的概率与该区域面积之比，当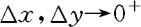时的极限值，这与物理量质量面密度是相通的。且当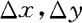充分小时，可得

即（X，Y）落在矩形区域D上的概率近似等于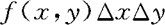，同时也表明f（x，y）是描述二元变量（X，Y）落在点（x，y）附近的概率大小的一个量。

例3.3.1　设二元随机变量（X，Y）的联合概率密度为

其中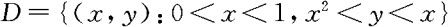。（1）求常数c；（2）求（X，Y）的联合分布函数；（3）求。

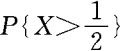解　（1）由联合概率密度性质（3）可知

得c＝15。

图3.3.1

（2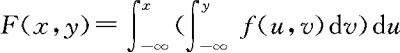），那么显然当x≤0或y≤0时，F（x，y）＝0；当x≥1且y≥1时，F（x，y）＝1。

图3.3.2

当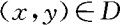（如图3.3.2）时，

图3.3.3

当（如图3.3.3）时，

同理可得，当0＜x＜1，y＞x时，

即

（3）记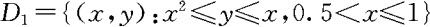，则

亦可，

（二）二元连续量的边际分布

设（X，Y）为二元连续量，F（x，y），f（x，y）分别为（X，Y）的联合分布函数及联合密度函数，称单个随机变量X（或Y）的密度函数为X（或Y的边际密度函数，且常分别用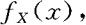 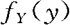表示。由于

那么由连续型随机变量的定义知，X为连续量，且X的概率密度函数为

即边际密度为联合密度关于另一个变量在（－∞，＋∞）上的积分。

例3.3.2　设二元随机变量（X，Y）的联合概率密度为

（1）求P｛X＋Y≥1｝的值；（2）求X的边际密度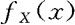；（3）求P｛X＞l/4｝的值。

解　（1）由题意得，

（2）当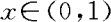时，

当。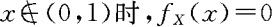

（3）由题意得，

（三）二元连续量的条件分布

图3.3.4

设（X，Y）为二元连续量，由条件分布函数的定义知，

在一定的条件下，，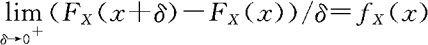

且

因此我们有下面的定义：

定义3.3.2　设（X，Y）为二元连续量，f（x，y）为（X，Y）的联合密度函数，为X，Y的边际密度函数。给定｛X＝x｝的条件下，Y的条件密度函数为

同样有

条件密度具有以下性质：（以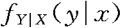为例）

（4）给定x，当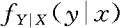在y处连续时，

以后，我们不一一说明地常用f（x，y）表示（X，Y）的联合密度，用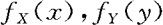分别表示X，Y的边际密度。

例3.3.3　设有一件事需甲，乙两人先后接力完成，完成时间要求不能超过30分钟。先由甲工作，再由乙接着干。设甲干了X（分钟），甲，乙两人共干了Y分钟，且设X服从（0，30）的均匀分布，Y服从（X，30）的均匀分布。（1）求（X，Y）的联合密度；（2）求条件密度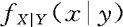；（3）当已知花了25分钟完成此事，求甲干的时间不超过10分钟的概率。

解　由题意知，X～U（0，30），即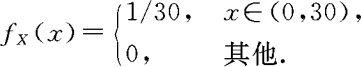由题意知，当甲干了x分钟结束时，Y服从（x，30）的均匀分布，故有，当0＜x＜30时，

由（3.3.4）知，

（2）由于，所以当0＜y＜30时，

当y取其他值时，。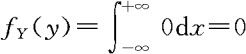

因此，当0＜y＜30时

（3）由题意知，所要求的是P｛X≤10｜Y＝25｝。当y＝25时，

因此

下面介绍两个重要的连续量。

定义3.3.3　设二元随机变量（X，Y）在二维有界区域D上取值，且具有联合概率密度

则称（X，Y）服从D上均匀分布。

若D1是D的一个子集，则可得到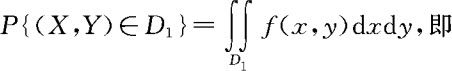

定义3.3.4　设二元随机变量（X，Y）具有联合概率密度（式中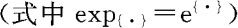

其中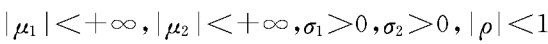，则称（X，Y）服从参数为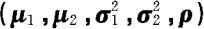的二元正态分布，记为。

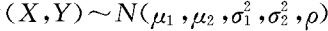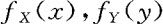例3.3.4　设二元随机变量（X，Y）在上均匀分布。（1）求关于X，Y的边际密度；（2）求给定X＝x（0＜x＜1）的条件下Y的条件密度；（3）求P｛Y≤X｝的值。

解　（1）因为（X，Y）在D上均勾分布，故（X，Y）具有联合密度为

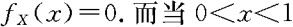又，那么显然，当x≤0或x≥1时，时，

即

（2）当0＜x＜1时，

图3.3.5

（3）由图3.3.5知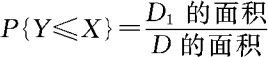，，其中。

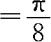D1的面积，D的面积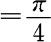，故。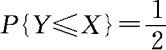

例3.3.5　设二元随机变量（X，Y）服从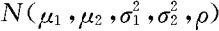分布。（1）求关于X，Y的边际密度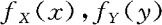；（2）求条件密度。

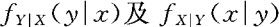解　（1）记，则

作积分变量变换，令，则

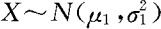即。同理可得。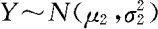

（2）根据条件密度的定义，知

同理可得

即当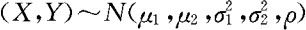时，X，Y的边际分布也是正态分布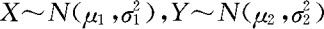，。当给定X＝x的条件下，Y的条件分布亦为正态分布，此时Y服从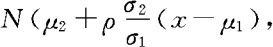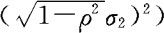。当给定Y＝y时，X的条件分布为。