从上一节的讨论可知,对总体同一参数,采用不同的估计方法得到的估计量可能是不一样的。在实际中如何选择“较好”的估计量呢?即如何评价估计量的优劣?本节将介绍四个评价准则:无偏性准则、有效性准则、均方误差准则和相合性准则。
(一)无偏性准则
估计量本身是统计量,其取值随着样本观察值的改变而改变。因此,我们不能根据某次抽样的结果来衡量估计量的好坏。一个自然评价标准是要求估计量无系统偏差,即要求在大量重复抽样时,所有估计值的平均应与待估参数的真值相同,这就是无偏性准则。具体定义如下。
定义7.2.1 设 是总体X的待估参数,X1,X2,…,Xn是来自总体X的样本。若估计量
是总体X的待估参数,X1,X2,…,Xn是来自总体X的样本。若估计量 的数学期望存在,满足
的数学期望存在,满足
则称 是θ的无偏估计量或无偏估计(unbiased estimator)。
是θ的无偏估计量或无偏估计(unbiased estimator)。
若 ,则称
,则称 为估计量
为估计量 的偏差。
的偏差。
若 ,但满足
,但满足 ,则称
,则称 是θ的渐近无偏枯计。
是θ的渐近无偏枯计。
例7.2.1 设总体X的均值μ和方差σ2存在,X1,X2,…,Xn是来自总体X的样本,证明:样本均值 和方差S2分别为μ和σ2的无偏估计。
和方差S2分别为μ和σ2的无偏估计。
证明 由X1,X2,…,Xn与X同分布且相互独立,得
和
因此,样本均值 和方差S2分别为μ和σ2的无偏估计。
和方差S2分别为μ和σ2的无偏估计。
若取σ2的估计量为 ,则有
,则有 ,但满足
,但满足
因此,B2是σ2的渐近无偏估计。
若取μ的估计量 ,其中权系数满足
,其中权系数满足 。则
。则 也是总体均值μ的无偏估计。我们称
也是总体均值μ的无偏估计。我们称 为参数μ的线性无偏估计。
为参数μ的线性无偏估计。
(二)有效性准则
由上面可知,在有些情况下,同一总体参数的无偏估计量是不唯一的。为比较两个无偏估计量的好坏,我们需进一步考察估计量取值的波动性,即估计量的方差。如果无偏估计量的方差越小,说明该估计量的取值越集中在参数真值的附近。
定义7.2.2 设 都是参数θ的无偏估计,若
都是参数θ的无偏估计,若
则称 比
比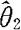 有效。
有效。
例7.2.2 讨论总体均值μ的线性无偏估计量 的有效性。
的有效性。
解 由于
且满足 。根据柯西—许瓦兹不等式知,在有关总体均值μ的所有线性无偏估计
。根据柯西—许瓦兹不等式知,在有关总体均值μ的所有线性无偏估计 中,当
中,当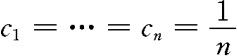 时,
时, 达到最小。即样本均值
达到最小。即样本均值 是总体均值μ的最有效线性无偏估计。
是总体均值μ的最有效线性无偏估计。
例7.2.3 设总体X服从区间[0,θ]上的均匀分布,其中θ是未知参数,若X1,X2,…,Xn是来自总体X的样本,试求参数θ的矩估计和极大似然估计,并讨论估计量的无偏性和有效性。
解 由E(X)=θ/2,可得θ的矩估计为 ,且
,且
因此 ,是θ的无偏估计。
,是θ的无偏估计。
根据例(7.1.7)可知,参数θ的极大似然估计为
为考察 的无偏性,先求X(n)的分布。由第三章第5节的知识,可求得X(n)的概率密度为
的无偏性,先求X(n)的分布。由第三章第5节的知识,可求得X(n)的概率密度为
因此 不是θ的无偏估计。但我们可以对
不是θ的无偏估计。但我们可以对 进行修正,令
进行修正,令 也是θ的无偏估计。
也是θ的无偏估计。
下面比较 的有效性。
的有效性。
由X(n)的分布可计算得
显然,当n⩾2时, ,因此
,因此 有效。
有效。
(三)均方误差准则
首先,我们给出均方误差的定义。
定义7.2.3 设 是总体参数θ的估计量,称
是总体参数θ的估计量,称 是估计量
是估计量 的均方误差,记为
的均方误差,记为 。
。
估计量 的均方误差越小,说明估计参数θ时的平均误差越小,因而也就越优。这就是均方误差准则。
的均方误差越小,说明估计参数θ时的平均误差越小,因而也就越优。这就是均方误差准则。
由定义可知,若 是参数θ的无偏估计量,则有
是参数θ的无偏估计量,则有 。此时,均方误差准则等价于有效性准则。
。此时,均方误差准则等价于有效性准则。
例7.2.4 设X1,X2,…,Xn是来自正态总体 的样本,由前面讨论知,样本方差S2是参数σ2的无偏估计,而样本二阶中心矩B2是σ2的有偏估计。现根据均方误差标准对这两个估计量作出评价。
的样本,由前面讨论知,样本方差S2是参数σ2的无偏估计,而样本二阶中心矩B2是σ2的有偏估计。现根据均方误差标准对这两个估计量作出评价。
解 根据S2的无偏性和 ,求得S2的均方误差
,求得S2的均方误差
下面计算B2的均方误差。
显然对任何n⩾2,有 。因此根据均方误差准则,以B2作为σ2的估计量要比S2更优。
。因此根据均方误差准则,以B2作为σ2的估计量要比S2更优。
在实际应用中,均方误差准则比无偏性准则更重要。
(四)相合性准则
前面三个准则都是在样本容量n固定的情况下讨论的。然而,由于估计量 依赖于样本容量n,自然会想到,一个好的估计量,当样本容量n越大时,该估计理应越精确越可靠,特别是当n→∞时,估计量的取值与参数真值应几乎完全一致,这就是估计量的相合性(或一致性)。相合性的严格定义如下。
依赖于样本容量n,自然会想到,一个好的估计量,当样本容量n越大时,该估计理应越精确越可靠,特别是当n→∞时,估计量的取值与参数真值应几乎完全一致,这就是估计量的相合性(或一致性)。相合性的严格定义如下。
定义7.2.4 设 是总体参数θ的估计量,若对任意ε>0,有
是总体参数θ的估计量,若对任意ε>0,有
即 依概率收敛于θ,则称
依概率收敛于θ,则称 是θ的相合估计量,并记为
是θ的相合估计量,并记为 。
。
一般地,由矩法求得参数的估计量都满足相合性,对于极大似然估计,则在总体分布满足一定正则的条件下,是待估参数的相合估计。
例7.2.5 X1,X2,…,Xn是来自均匀分布U[0,θ]的样本,证明由例7.2.3给出的两个估计量 都是参数θ的相合估计。
都是参数θ的相合估计。
证明 根据例7.2.3的结果有
根据切比雪夫不等式,对任意ε>0,有
因此, 是参数θ的相合估计。
是参数θ的相合估计。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















