设正态总体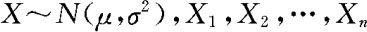 是来自该总体的样本,记
是来自该总体的样本,记
(一)有关参数μ的假设检验
1.σ2已知
先考虑双边假设问题
其中μ0是已知的常量。根据前一节的讨论,此时我们可取检验统计量为
当原假设H0成立,即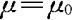 时,Z~N(0,1)。根据奈曼—皮尔逊原则,在给定的显著水平α下,检验的拒绝域为
时,Z~N(0,1)。根据奈曼—皮尔逊原则,在给定的显著水平α下,检验的拒绝域为
对给定样本观察值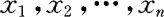 ,当检验统计量Z的取值的绝对值
,当检验统计量Z的取值的绝对值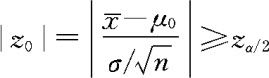 时,作出拒绝原假设的判断,即认为根据当前样本资料,我们有100(1-α)%的把握认为
时,作出拒绝原假设的判断,即认为根据当前样本资料,我们有100(1-α)%的把握认为 ,否则,接受原假设。
,否则,接受原假设。
另外,我们也可通过计算P_值来作出判断,其中
当P_值小于给定的显著水平α时,拒绝原假设,否则,接受原假设。
对于左边假设问题
检验统计量仍为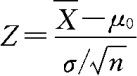 。当原假设H0成立,即
。当原假设H0成立,即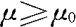 时,Z取值偏大,因此拒绝域的形式为
时,Z取值偏大,因此拒绝域的形式为
其中临界值C满足奈曼—皮尔逊原则。首先我们来计算犯第Ⅰ类错误的概率。
注意到此时Z不服从标准正态分布,而是有
显然,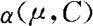 关于μ是严格减函数,为使犯第Ⅰ类错误的概率不超过给定的显著水平α,需满足
关于μ是严格减函数,为使犯第Ⅰ类错误的概率不超过给定的显著水平α,需满足
又根据奈曼—皮尔逊原则,当上式中等号成立时,犯第II类错误的概率最小。因此,应取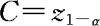
 ,从而左边假设问题检验的拒绝域为
,从而左边假设问题检验的拒绝域为
此时,P_值可由下式计算得到
类似地,对于右边假设问题
我们可推得检验的拒绝域为
上述检验,我们通常称为Z检验。
例8.2.1 据健康统计中心报告35至44岁的男子平均心脏收缩压为128,标准差为15。某公司的健康主管观察了该公司在33至44岁年龄段的72位管理人员的体检记录,发现他们的平均心脏收缩压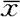 为126.07(mm/Hg)。这是否意味着该公司管理人员的心脏收缩压与一般的人群有显著差异?(显著水平α=0.05)现在假设这些管理人员的心脏收缩压服从正态分布,且与一般中年男子的心脏收缩压具有相同的标准差σ=15。
为126.07(mm/Hg)。这是否意味着该公司管理人员的心脏收缩压与一般的人群有显著差异?(显著水平α=0.05)现在假设这些管理人员的心脏收缩压服从正态分布,且与一般中年男子的心脏收缩压具有相同的标准差σ=15。
解 设随机变量X为中年男子的心脏收缩压,由已知条件,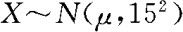 。下面我们根据假设检验问题的处理步骤来讨论该公司管理人员的心脏收缩压是杏与一般的人群有显著差异。
。下面我们根据假设检验问题的处理步骤来讨论该公司管理人员的心脏收缩压是杏与一般的人群有显著差异。
步骤1:提出假设
设原假设为该公司管理人员的平均心脏收缩压与全国中年男子的平均收缩压无差异,即μ=128。由于健康主管没有要求比较这两者的大小,故备择假设是双边的,所以提出的假设为
步骤2:提出检验统计量
由上面讨论可知,检验统计量可取为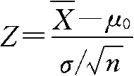 ,其中
,其中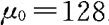 。
。
步骤3:给出拒绝域
在显著水平α=0.05下,由(8.2.1)得检验的拒绝域为
步骤4:判断
由样本资料可计算得检验统计量的观察值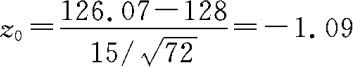 ,显然,
,显然,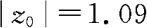
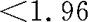 ,因此,我们作出接受原假设的判断,即认为该公司管理人员的心脏收缩压与一般的人群没有显著差异,
,因此,我们作出接受原假设的判断,即认为该公司管理人员的心脏收缩压与一般的人群没有显著差异,
若要通过计算P_值来作出判断,则步骤3和4转为:
步骤3′:计算检验统计量的观察值和P_值
由样本资料可计算得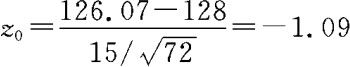 。则由(8.2.2)有
。则由(8.2.2)有
步骤4′:判断
由于P_>α=0.05,所以我们认为统计不显著,即认为该公司管理人员的心脏收缩压与一般的人群没有显著差异。
2.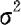 未知
未知
在实际应用中,参数 常常是未知的,此时,我们不能采用Z检验,需要用样本方差
常常是未知的,此时,我们不能采用Z检验,需要用样本方差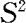 来代替
来代替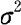 ,从而得到检验统计量
,从而得到检验统计量
类似于前面的讨论,为给出拒绝域或计算P_值,我们只需知道当 时T的分布,根据抽样分布定理6.3.3有
时T的分布,根据抽样分布定理6.3.3有
在给定样本观察值 时,检验统计量的取值为
时,检验统计量的取值为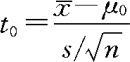 。根据t分布,我们可给出相应的拒绝域和P_值的计算。
。根据t分布,我们可给出相应的拒绝域和P_值的计算。
上述检验,我们通常称为t检验。在实际应用中,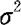 通常是未知的,因此,t检验要比Z检验应用更广泛。
通常是未知的,因此,t检验要比Z检验应用更广泛。
例8.2.2 在某高校某个班级拥有手机的同学中随机抽取25名,以了解手机话费支出情况,调查得到月平均话费支出66.45元,标准差为20.32元。假设手机话费X服从正态分布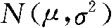 ,问是否有充分的理由认为该班拥有手机的同学的月平均话费支出大于60元?
,问是否有充分的理由认为该班拥有手机的同学的月平均话费支出大于60元?
解 由样本资料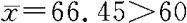 ,我们需要将希望得到支持的假设“μ>60”作为备择假设,即考虑右边假设问题
,我们需要将希望得到支持的假设“μ>60”作为备择假设,即考虑右边假设问题
因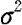 未知,取检验统计量为
未知,取检验统计量为
将样本资料n=25,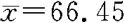 ,s=20.32和
,s=20.32和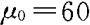 代入,得观察值为
代入,得观察值为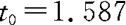 。
。
查t分布表,得 。因此,如果取显著水平α=0.05,我们应作出接受原假设的判断,即认为该班拥有手机的同学的月平均话费支出不超过60元,但如果取显著水平α=0.1,则我们应拒绝原假设。
。因此,如果取显著水平α=0.05,我们应作出接受原假设的判断,即认为该班拥有手机的同学的月平均话费支出不超过60元,但如果取显著水平α=0.1,则我们应拒绝原假设。
利用Excel可计算得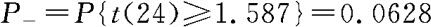 。显然,0.05<P_<0.1,可作出同样的判断。实际上,P_值告诉我们,根据目前的资料,有93,72%的把握认为该班拥有手机的同学的月平均话费支出超过60元。
。显然,0.05<P_<0.1,可作出同样的判断。实际上,P_值告诉我们,根据目前的资料,有93,72%的把握认为该班拥有手机的同学的月平均话费支出超过60元。
(二)成对数据的t检验
成对数据问题在7.4节中已作过介绍。现在我们用假设检验的思想来考察某种降血压药的效果。假设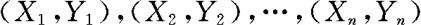 分别是n个高血压病人在服药前后的血压测量值,差值
分别是n个高血压病人在服药前后的血压测量值,差值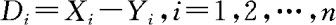 可以看成来自正态总体
可以看成来自正态总体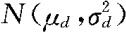 的样本。为检验降血压是否有效,就归结为检验如下假设问题
的样本。为检验降血压是否有效,就归结为检验如下假设问题
于是问题就变成了有关单个正态总体的均值的假设检验。记
对于双边假设和左边假设问题,我们也可以类似讨论。
例8.2.3 对某品牌矿泉水进行水质分析,随机抽取500mL装的8瓶,将每瓶各一半的水分别送到两个不同实验室进行检测,下面是两个实验室对8瓶水中钾元素含量的测定结果(单位:μg/100mL):
假设两实验室的检测结果之差服从正态分布,试检验这两个实验室的检测结果是否有显著差异?
解 设产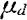 为两个实验室对水中钾元素含量的测定结果的平均差值,考虑双边假设:
为两个实验室对水中钾元素含量的测定结果的平均差值,考虑双边假设:
由已知资料得两实验室测定结果的差值观察值为
且有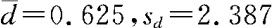 。
。
将上述结果代入检验统计量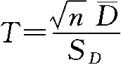 ,得观察值为
,得观察值为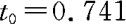 。利用Excel计算P_值为
。利用Excel计算P_值为
因此,我们没有充分的理由认为两实验室测量结果有显著差异。
Excel中TTEST函数可以计算成对数据的检验,具体步骤如下:
(1)将实验室A,B的数据输入Excel表中,设数据区域分别为A1:A8和B1:B8;
(2)在Excel表中任选一空白单元格(例如:C1单元格)下拉菜单“插入”选项卡 单击“函数”
单击“函数” 在类别的下拉式菜单中,选择“统计”选项
在类别的下拉式菜单中,选择“统计”选项 选择“TTEST”
选择“TTEST” 在弹出的对话框的“Arrayl”文本框中输入“A1:A8”,“Array2”文本框中输入“B1:B8”,“Tails”文本框中输入“2”(“1”代表单尾概率),“Type”本框中输入“1”(“2”代表两样本等方差,“3”代表两样本异方差)
在弹出的对话框的“Arrayl”文本框中输入“A1:A8”,“Array2”文本框中输入“B1:B8”,“Tails”文本框中输入“2”(“1”代表单尾概率),“Type”本框中输入“1”(“2”代表两样本等方差,“3”代表两样本异方差) 点击Enter键
点击Enter键 C1单元格即可显示P_值为“0.482994”。
C1单元格即可显示P_值为“0.482994”。
(三)有关参数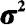 的假设检验
的假设检验
这里,我们不妨假设参数μ是未知的,其假设问题包括
其中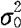 是已知的常量。此时
是已知的常量。此时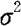 的无偏估计量
的无偏估计量
且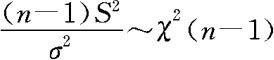 。因此,我们可取检验统计量为
。因此,我们可取检验统计量为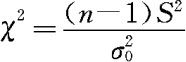 。类似于前面的讨论,只需知道当
。类似于前面的讨论,只需知道当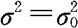 时,检验统计量
时,检验统计量 的分布。显然,此时有
的分布。显然,此时有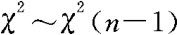 。在给定显著水平α时,我们有检验拒绝域:
。在给定显著水平α时,我们有检验拒绝域:
双边检验: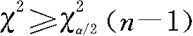 ,或
,或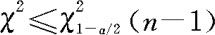 ;
;
左边检验: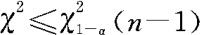 ;
;
右边检验: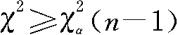 。
。
与均值检验相同,我们也可通过计算P_值来判断是否拒绝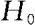 ,当P_值小于给定的显著水平α时,拒绝原假设;否则,接受原假设。关于P_值的计算方法与均值检验的方法类似。我们通常称上述检验为
,当P_值小于给定的显著水平α时,拒绝原假设;否则,接受原假设。关于P_值的计算方法与均值检验的方法类似。我们通常称上述检验为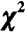 检验。
检验。
下面我们来解答例8.1.2,这是关于正态总体方差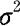 的假设检验问题,需检验下列假设
的假设检验问题,需检验下列假设
根据已知资料,计算得到检验统计量的取值为
查表可得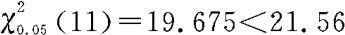 。因此,我们拒绝原假设,即至少有95%的把握认为该种摄影药品的贮藏寿命的标准差大于10天。
。因此,我们拒绝原假设,即至少有95%的把握认为该种摄影药品的贮藏寿命的标准差大于10天。
另,我们也可利用Excel计算得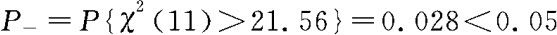 ,作出同样的判断。
,作出同样的判断。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















