定义和例子

定义10.1.1　设S是样本空间，P是概率，。如果对任何是S上的随机变量，则称是S上的随机过程（stochastic process），T称为参数集。

用映射来表示：

即X（·，·）是定义在T×S上的二元单值函数。固定t，X（t，·）是S上的随机变量；固定e，X（·，e）是T的函数，称为随机过程的样本函数或样本轨道（sample path），或随机过程的一个实现。取遍，X（t）的所有可能取值全体称为状态空间（states pace），记为I.

以后X（t，e）也记为Xt（e）。很多情况下，T可以理解为时间参数，如果T至多可列，则称为离散时间，否则为连续时间。常用的T有：，其中（1），（2）属于离散时间，（4），（5）属于连续时间。

状态空间如果至多可列，则称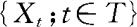为离散状态随机过程，否则称为连续状态随机过程。这样按照时间参数和状态空间，随机过程可分成四类：（1）离散时间离散状态；（2）离散时间连续状态；（3）连续时间离散状态；（4）连续时间连续状态。

例10.1.1　（二项过程）某人在打靶，每次命中率是p，且设各次的结果相互独立。用Sn表示前n次命中的次数，则是一个离散时间离散状态的随机过程，它的状态空间。

例10.1.2　（Z上的随机游动）甲乙两人在玩一种游戏，每次甲赢一元的概率是p，输一元的概率为1－p，且设各次的输赢结果相互独立。用Sn表示前n次甲赢的钱数，则{Sn；n＝0，1，2，…}是一个离散时间离散状态的随机过程，它的状态空间。这样的过程称为Z上的随机游动。

特别地，当时，称｛Sn｝为Z上的对称随机游动。

例10.1.3　考虑到某商场消费的情况，第i人消费的钱数记为Xi。设X1，…，Xn，…独立同分布，令Sn表示前n人消费的总钱数，则｛Sn；n＝0，1，2，…｝是一个离散时过程。且.这样的过程称为R上的随机游动。

例10.1.4　（随机相位正弦波）考虑这里α，ω是正常数，。

则｛X（t）}是连续时间连续状态的随机过程，状态空间I＝［－α，α］。这里Θ可理解为初始相位，它服从［0，2π］上的均匀分布。一旦初始相位确定，则整个过程就完全确定。所有的样本函数是

这族样本函数的不同就在于初始相位θ的不同。

图10.1.1给出了当时对应的3条样本函数。

图10.1.1

例10.1.5　考虑（0，t］内到某保险公司进行索赔的人数，记为N（t），则｛N（t）；t≥0｝是一个连续时间离散状态的随机过程，状态空间I＝{0，1，2，…｝。假设不会有两人或两人以上同时索赔，设第i人索赔的时刻为ti，则0＜tl＜t2＜…，对应的样本函数如图10.1.2所示。

图10.1.2

例10.1.6　考虑

这里ω是正常数，V～U［0,1］。

则｛X（t）｝是连续时间连续状态的随机过程，状态空间I＝[－1，1]，一旦振幅V确定，则整个过程就完全确定。所有的样本函数是。这族样本函数的不同就在于振幅v的不同。图10.1.3给出了当，1时对应的2条样本函数。

图10.1.3

随机过程在任一时刻的状态是随机变量，因此可以利用随机变量的描述方法即分布函数和数字特征等方法来描述随机过程的统计特性。