均值函数和协方差函数

对于随机过程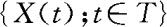，除了研究它的有限维分布族外，我们也可以研究它的一些数字特征，如均值函数，协方差函数，等等。以下定义都是假设它们存在的条件下给出的。

定义10.3.1　对任何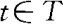，定义

它们都是参数t的函数，分别称为随机过程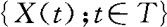的均值函数，均方值函数几，方差函数和标准差函数。

对任何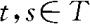，定义

则Rx和Cx是定义在T×T上的函数，分别称为随机过程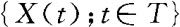的（自）相关函数和（自）协方差函数。

显然。另外Rx和Cx都是对称函数，即。

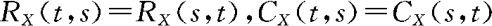现在来考虑一些特殊的过程。如果对任何存在，则称随机过程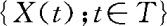是二阶矩过程，由Cauchy-Schwarz不等式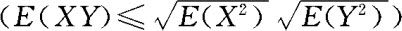知，二阶矩过程的均值函数，相关函数，协方差函数都是存在的。

例10.3.1　计算随机相位正弦波

是正常数的均值函数，方差函数，自相关函数和自协方差函数。

解

例10.3.2　设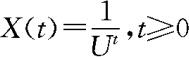，这里U～U（0,1）。请问{X（t）；t≥0}是否是二阶矩过程？

解　对任何t≥0，

所以{X（t）；t≥0}不是二阶矩过程。

设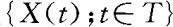是一随机过程，如果对任意n，任何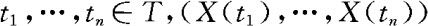服从正态分布，则称是正态过程（或高斯过程）（Gaussian process）。正态过程是二阶矩过程，它的有限维分布完全由它的均值函数和自协方差函数确定。

例10.3.3　设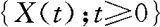是正态过程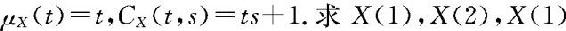，的分布。

解　因为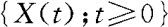是正态过程，。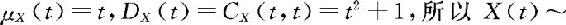

因为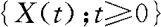是正态过程，所以（X（1），X（2））服从正态分布，因此X（1）十X（2）服从正态分布。而。

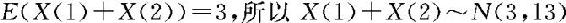例10.3.4　设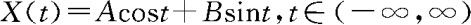，这里随机变量A和B相互独立，且。

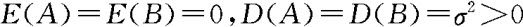（1）计算｛X（t）｝的均值函数，自相关函数和自协方差函数。

（2）若的分布律。

（3）若A，B～N（0，σ2），证明｛X（t）｝是正态过程，并分别求出的分布。

解

（3）若A，～N（0，σ2），因为A和B独立，所以二维随机变量（A，B）服从正态分布，对任意n，任何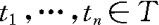，由于对任何i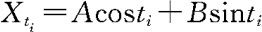，是（A，B）的线性组合，根据正态分布的线性变换不变性，n维随机变量也服从正态分布。所以{X（t）｝是正态过程。

因为是正态过程，所以对任何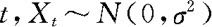。特别地，。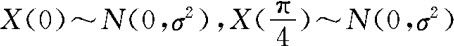

而。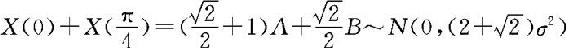

下面考虑两个随机过程之间的关系。

定义10.3.2

它们是T×T上的函数，分别称为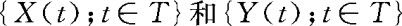的互相关函数和互协方差函数。

如果对任何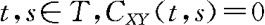，则称过程｛X（t）｝和｛Y（t）｝不相关。

如果对任何m，n，任何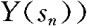独立，则称过程｛X（t）｝和｛Y（t）｝相互独立。

一般地，过程不相关，不能推出它们相互独立。但如果它们相互独立，且都是二阶矩过程，则它们一定不相关。

例10.3.5　设某保险公司的收入由老人寿险收入和儿童平安保险收入组成。设到时刻t为止，老人寿险收入为X（t），儿童平安保险收入为Y（t），保险公司总收入为Z（t）。已知μx（t），μy（t），CX（t，s），CY（t，s），{X（t）；t＞0｝和｛Y（t）；i＞0｝不相关，求{Z（t）；t＞0｝的均值函数和协方差函数。

解　由题可知Z（t）＝X（t）＋Y（t）,所以