马尔可夫链的定义

本章中牵涉到的条件概率都是在P（B）＞0的条件下。

定义11.1.1　设随机过程｛Xn；n＝0，1，…｝的状态空间I有限或可列，如果它具有马尔可夫（Markov）性，即对任何n≥1，任何有

则称｛Xn；n＝0，1，…）是马尔可夫（Markov chain）链。

状态空间有限的Markov链称为有限Markov链。

若以n代表现在的时刻，记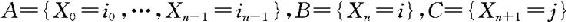。则A代表过去，B代表现在，C代表将来，（11.1.1）式为。因此Markov性的直观含义是当知道到现在为止的所有状态，则将来的分布只与现在有关，而与过去无关，就好像忘记了它过去的轨迹，所以Markov性也称为无记忆性。因为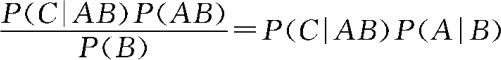，所以（11.1.1）式等价于

因此Markov性也可以理解为在知道现在状态的条件下，过去与将来相互独立。

另外Markov性也等价于对任何有

记为m时处于状态i的条件下，经过n步后转移到状态j的转移概率，则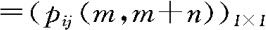为对应的n步转移矩阵，则它所有元素非负，且每一行的元素之和为1。

如果不依赖于n，则称｛Xn｝是时间齐次（或时齐）的Markov链，pij称为从i到j的一步转移概率（one-step transition probability）。显然。令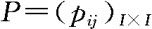为一步转移矩阵。对于时齐Markov链，也可用状态转移图来表示一步转移概率，用来表示状态i，如果pij＞0，则用箭头从i连到j，并在箭头上标上pij，状态转移图可以让我们对过程的演化有一个直观的认识。

例11.1.1　（0-1传输系统）（见图11.1.1）

图11.1.1

如上图只传输0和1的串联传输系统中，设每一级的传真率（输入输出一致的概率）为p，误码率（输入输出不同的概率）为q=1-p。以X0表示第一级的输入，Xn表示第n级的输出（n≥1）。则｛Xn｝是一时间齐次的Markov链，状态空间是I={0，1}，一步转移矩阵为

图11.1.2

对应的状态转移图见图11.1.2.

例11.1.2　（Ehrenfest模型）（见图11.1.3）

图11.1.3

如图11.1.3所示容器A，B共有m（m≥1）个跳蚤，假设每次随机地有一个跳蚤从一个容器跳到另一个容器，令Xn表示n次后容器A内的跳蚤数，则｛Xn}是时齐的Markov链，状态空间是I={0，1，…，m}，

例11.1.3　（一维随机游动）甲乙两人玩游戏，每一局甲赢一元的概率为p，输一元的概率为q=1-p，0＜p＜1。假设一开始甲带了0元钱。令Sn表示n局后甲所拥有的总钱数。则｛Sn｝是时齐的Markov链，状态空间I={…，-2，-1，0，1，2…｝，

状态转移图见图11.1.4。

图11.1.4

例11.1.4　（图上的简单随机游动）设V是一个简单图的顶点集合，对任何，如果ij有边相连，则称j是i的邻居。假设每个顶点至少有一个邻居。现在有一个粒子在V上跳动，如果第n步在顶点i的话，则下一步等可能地到达i的邻居。以Xn表示n步后粒子所在的顶点，则{Xn｝是时齐的Markov链，状态空间I=V，若j不是i的邻居，则pij=0，若j是i的邻居，则若j是i的邻居，则，这里di表示i的邻居数。

图11.1.5上的简单随机游动对应的状态空间I={0，1，2，3}，

图11.1.5

图11.1.6

例11.1.5　如图11.1.6所示，由两块相同设备平行组成的系统。两设备独立工作，每天的可靠性为（即在一天里坏掉的概率为1-α），一开始两块设备正常工作，以Xn表示第n天结束时正常工作的块数，则{Xn；n≥0}是时齐Markov链，I={0，1，2}，

图11.1.7

状态转移图如图11.1.7所示。

例11.1.6　某商店为保证商品的连续供应，在时刻tn（n≥0）检查，如货存小于等于a，则补充到b（a＜b），否则不补充。这里a，b都是正整数。用Xn表示在时刻tn检查前的货存，用Yn表示在时间区间［tn-1，tn］内的需求量。则

设X0∊{0，1，…，b}，Y1，Y2…独立同分布，Y1的分布律为P（Y1=i）=pi；i=0，1，2，...。则｛Xn｝是一时齐Markov链，状态空间I={0，1，…，b}，一步转移概率

设｛Xn｝是一时齐Markov链，i是一状态，如果pii=1，则称状态i是一吸收态。Markov链一旦进入吸收态i，则它将永远呆在状态i。当Markov链有好几个吸收态时，我们有时会关心被其中某个吸收态吸收的概率，比如经典的赌徒输光问题（见例11.1.7）和迷宫中的老鼠问题（见习题6）。

例11.1.7　（赌徒输光问题）甲乙两人玩抛硬币游戏，一开始甲带有a元钱，乙带有m-a元钱，a，m-a都是非负整数，m＞0。甲独立重复地扔一枚均匀的硬币，如果第n次硬币出现正面，则第n次甲赢一元，否则甲输一元。游戏一直到某人输光为止。计算最后甲输光的概率。

解　令Sn表示扔n次硬币后甲所拥有的钱数，则｛Sn｝是一个时齐Markov链，状态空间是｛0，1，…，m}，一步转移概率为。对应的状态转移图如图11.1.8所示。

图11.1.8

此Markov链有两个吸收态0和m。令T0=inf{n≥0：Sn=0}，即首次访问状态0的时刻。记ha=P（T0＜∞｜S0=a），则所求的输光概率为P（甲输光｜S0=a）=ha，即最终被0吸收的概率。显然，h0=1，hm=0。

对0＜a＜m，游戏至少需进行一次，这一次之后甲的钱数有的概率变成a+1，有的概率变成a-1。如果一次之后甲的钱数变为j的话，则由于Markov性，最终输光的概率就好像一开始甲带j元钱而最终输光的概率（见图11.1.9）。

图11.1.9

所以由全概率公式和Markov性，得

即。由此推出。这也说明带的钱越少，输光的概率就越大，这与人们的直观是吻合的。

例11.1.8　设｛Xn｝是时齐的Markov链，状态空何I={1，2，3，4}，一步转移矩阵。令，即hi表示从i出发在有限时间内能访问状态3的概率。求h1和h2。

解　显然h3=1，h4=0，对i=1，2，