设{Xn}是一时齐Markov链,i是某一状态。定义
为i的首中时(约定infφ=∞)。如果P(τi<∞|X0=i)=1,则称i常返(recurrent),否则称i暂留(transient)。如果i常返,则令μi=E(τi|X0=i),称为状态i的平均回转时。如果μi<∞则称i正常返=(positive recurrent),否则称i零常返(null recurrent)。如果所有状态都是常返(暂留,零常返,正常返)的,则称此Markov链常返(暂留,零常返,正常返)。
令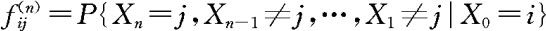 ,表示从i出发第n步首次击中j的概率。令fij=P(τi<∞|X0=i),表示从i出发在有限步能击中j的概率,则
,表示从i出发第n步首次击中j的概率。令fij=P(τi<∞|X0=i),表示从i出发在有限步能击中j的概率,则 。所以状态i常返当且仅当fii=1。若i常返,则
。所以状态i常返当且仅当fii=1。若i常返,则 。
。
例11.3.1 假设{Xn}是时齐Markov链,状态空间为I={0,1,2,3},一步转移矩阵为
讨论状态0和状态3的常返性。
解 对于状态 。
。
当≥4时, 。所以
。所以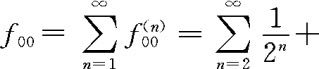
 。这说明0是一个常返态。进一步地,
。这说明0是一个常返态。进一步地, ,所以0是正常返态。
,所以0是正常返态。
对于状态3, 。因此3也是正常返态。
。因此3也是正常返态。
例11.3.2 (爬梯子模型)假设{Xn}是时齐Markov链,状态空间为I={0,1,2,…}, 。讨论状态0的常返性。
。讨论状态0的常返性。
解:状态转移图为
所以0是常返态当且仅当 。
。
进一步地,如果0是常返态,则
所以0是正常返态当且仅当 。
。
例如,如果 ,此时0是暂留态。
,此时0是暂留态。
如果 ,所以0是零常返态。
,所以0是零常返态。
如果 ,所以0是正常返态。
,所以0是正常返态。
下面讨论常返性的一些等价描述。设i是某状态,令Ni=#{n≥0:Xn=i}表示访问i的次数。
定理11.3.1 (1)i常返当且仅当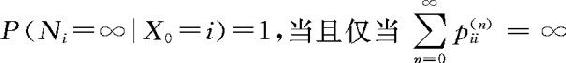 。
。
(2)i暂留当且仅当 。
。
证明 首先 。其次,令
。其次,令 ,表示事件“第l步首次击中i,第m+l步第二次击中i”,则
,表示事件“第l步首次击中i,第m+l步第二次击中i”,则
对任何l,m≥1,由乘法公式,Markov性和时齐性,
同理可证,对任何 。如果fii=1,则
。如果fii=1,则
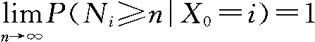 ;如果fii<1,则
;如果fii<1,则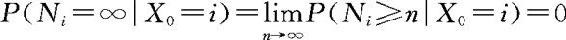 。
。
另一方面如果fii<1,则对任何n≥1,
即如果Markov链从i出发,则访问i的次数服从参数为1-fii的几何分布,从而
 。令
。令
则 ,所以
,所以 表示Markov链从i出发访问状态i的平均次数。所以如果i常返,则
表示Markov链从i出发访问状态i的平均次数。所以如果i常返,则 ,如果i暂留,则
,如果i暂留,则
 。
。
上面定理说明i常返当且仅当从i出发以概率1无穷多次返回状态i,即“经常返回”;而i暂留则意味着以概率1返回i次数有限,即在i处“短暂逗留”后将永不再返回i。
在例11.3.1中,我们已讨论了状态0和状态3的常返性,那么状态1和2的常返性又是如何呢?让我们一起来计算一下 ,可是你会发现这个计算很复杂。那么还有什么好方法来判断呢?有,这就是接下来要讲的利用互达的关系来判断。
,可是你会发现这个计算很复杂。那么还有什么好方法来判断呢?有,这就是接下来要讲的利用互达的关系来判断。
设i,j是两状态,称i可达j,记为 ,如果i=j,或存在n≥1,使得
,如果i=j,或存在n≥1,使得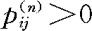 。如果
。如果 且
且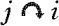 ,则称i,j互达(Communicate),记为
,则称i,j互达(Communicate),记为 。可证明↔满足以下三条:(1)自反性:
。可证明↔满足以下三条:(1)自反性: ;(2)对称性:如
;(2)对称性:如 ;(3)传递性;如
;(3)传递性;如 .
.
所以互达是一个等价关系。于是状态空间可表示成互不相交的互达等价类的并。如果状态空间中任何两个状态互达,则称此Markov链不可约。
定义状态i的周期(period)d(i)为集合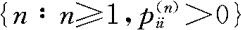 中的最大公约数(若该集合为空集,则定义d(i)=0)。显然,如果
中的最大公约数(若该集合为空集,则定义d(i)=0)。显然,如果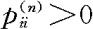 ,则n一定是d(i)的整数倍。也就是说从i出发只有在d(i)的整数倍步数后,才有可能以正概率返回i。如果d(i)=1,则称i非周期。如果所有i非周期(aperiodic),则称此Markov链非周期。若状态i正常返且非周期,则称i为遍历状态。不可约非周期正常返的Markov链称为遍历的Markov链(ergodic Markov chain)。
,则n一定是d(i)的整数倍。也就是说从i出发只有在d(i)的整数倍步数后,才有可能以正概率返回i。如果d(i)=1,则称i非周期。如果所有i非周期(aperiodic),则称此Markov链非周期。若状态i正常返且非周期,则称i为遍历状态。不可约非周期正常返的Markov链称为遍历的Markov链(ergodic Markov chain)。
例11.3.3 设{Xn}是时齐Markov链,状态空间I={0,1,2,3,4,5},一步转移矩阵
求出所有互达等价类,各状态的周期和常返性。
解 状态转移图为
共有四个互达等价类:{0},{1,2},{3,4},{5}。
状态0是吸收态。因为p00=1,所以d(0)=1,且 ,从而μ0=1,所以0也是正常返态。
,从而μ0=1,所以0也是正常返态。
因为 ,所以
,所以
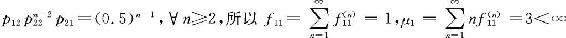 。因此1是正常返态。
。因此1是正常返态。
因为p22>0,所以 ∞。因此2是正常返态。
∞。因此2是正常返态。
因为 当且仅当n是偶数,所以
当且仅当n是偶数,所以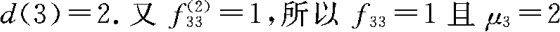 ,因此3是正常返态。同理d(4)=2,4是正常返态,且μ4=2。
,因此3是正常返态。同理d(4)=2,4是正常返态,且μ4=2。
因为p55>0,所以 。因此5是暂留态。
。因此5是暂留态。
定理11.3.2 如果 ,则:(1)d(i)=d(j);(2)i常返当且仅当j常返;(3)i正常返当且仅当j正常返。
,则:(1)d(i)=d(j);(2)i常返当且仅当j常返;(3)i正常返当且仅当j正常返。
这个定理告诉我们在同一个互达等价类中,各状态具有相同的周期和常返性。例如在上例中,1,2互达,所以它们具有相同的周期和常返性。同样3,4互达,所以它们具有相同的周期和常返性。因此在判断一个状态的性质时,我们可以从它的等价类中找到一个容易判断的状态来进行判断。特别地,不可约Markov链中各状态性质相同,所以此Markov链或者为暂留,或者为零常返,或者为正常返。现在就可以利用这个定理来讨论例11.3.1中状态1和2的常返性了。
例11.3.4 讨论例11.3.1中和例11.3.2中各状态的周期和常返性。
解 例11.3.1中,各状态互达,因为状态0是正常返的,所以所有的状态都是正常返的;因为p33>0,所以d(3)=1,所以d(0)=d(1)=d(2)=d(3)=1。这是一个不可约非周期正常返的Markov链。
例11.3.2中,各状态互达,因为p00>0,所以d(0)=1,所以各状态周期为1。这是一个不可约非周期的Markov链。各状态的常返性与状态0的常返性相同。所以
(1)当 时,各状态暂留;
时,各状态暂留;
(2)当 ,各状态零常返;
,各状态零常返;
(3)当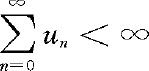 时,各状态正常返。
时,各状态正常返。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















