线性系统是工程应用中最常见的一类系统,在一个线性系统中如果输入一个平稳过程,那么输出的随机过程平稳吗?输入过程与输出过程的相关性又是怎祥的呢?这些就是本节要考虑的问题。

图13.4.1
系统的输入输出间关系可以如图13.4.1所示。
其中二x(t)代表输入,y(t)代表输出,算子L代表系统的作用,它们的关系为

(一)线性时不变系统
定义13.4.1 对于系统L,设
若对于任意常数α,β,有

则称L为线性系统。
定义13.4.2 对于系统L,设 。若对于任一时间平移τ。有
。若对于任一时间平移τ。有

则称L为时不变系统或定常系统。
例13.4.1 微分算子 是线性时不变的。
是线性时不变的。

所以,微分算子是线性时不变系统。
例13.4.2 积分算子 是线性时不变的。
是线性时不变的。

所以,积分算子是线性时不变系统。
由定义可知,系统的线性性质表现在该系统满足叠加原理,系统的时不变性质表现在输出对输入的关系不随时间的推移而改变。在工程应用中,属于这类较简单而又十分重要的系统是输入与输出之间可以用常系数线性微分方程来描述的系统:

其中 。
。
(二)频率响应与脉冲响应
定理13.4.1 设L为线性时不变系统,若输入一个谐波信号 ,则输出为
,则输出为 ,其中
,其中 。
。
证明 令 ,由系统的线性时不变性,对固定的τ和任意的t,有
,由系统的线性时不变性,对固定的τ和任意的t,有

令 。
。
定理表明,对线性时不变系统输入谐波信号时,其输出也是同频率的谐波,只是振幅和相位有变化,而H(ω)表示了这一变化,将H(ω)称为系统的频率响应函数。
例如,对于微分算子 ,系统的频率响应函数
,系统的频率响应函数 。
。
一般地,对于输入x(t),根据δ函数的性质, ,于是,输出
,于是,输出

其中 。
。
若输入x(t)为表示脉冲的δ函数,即 ,则输出为
,则输出为

因此将h(t)称为系统的脉冲响应函数。
注意到,经过变量替换有

这表明,从时间域分析,线性时不变系统的输出y(t)是输入x(t)与脉冲响应h(t)的卷积。若设输入x(t),输出y(t)和脉冲响应h(t)都满足傅立叶变换条件,且相应的傅立叶变换分别为, ,即
,即

则 。
。
可以证明: ,也就是频率响应函数H(w)即为脉冲响应h(t)的傅立叶变换。
,也就是频率响应函数H(w)即为脉冲响应h(t)的傅立叶变换。

这表明,从频率域分析,线性时不变系统输出响应的傅立叶变换Y(ω)是输入的傅立叶变换X(ω)与系统脉冲响应的傅立叶变换即频率响应函数H(ω)的乘积。
实际应用中常假定当t<0时,h(t)=0。相应地,

(三)线性系统输出过程的均值和相关函数
设系统输入的平稳过程为X(t),且对于X(t)的任一样本函数x(t),有

也是随机过程。下面讨论输入过程X(t)的均值和相关函数与输出过程的均值和相关函数的关系。
定理13.4.2 设输入平稳过程X(t)的均值为μX,自相关函数为RX(τ),则输出过程Y(t)也是平稳过程,且X(t),Y(t)是联合平稳的。其数字特征有

从中可以看出,Y(t)是平稳过程,且X(t),Y(t)是联合平稳的。
例13.4.3 设线性系统输入一个白噪声过程X(t),即均值为 ,自相关函数为
,自相关函数为

由此可得, ,即可以从实测的互相关函数资料估计线性系统未知的脉冲响应。
,即可以从实测的互相关函数资料估计线性系统未知的脉冲响应。
(四)线性系统的功率谱密度
定理13.4.3 设系统输入过程为X(t),输出过程 是联合平稳的。其中X(t)具有谱密度SX(ω),系统的频率响应函数为H(ω)。则Y(t)的谱密度为
是联合平稳的。其中X(t)具有谱密度SX(ω),系统的频率响应函数为H(ω)。则Y(t)的谱密度为 的互谱密度为
的互谱密度为 ,
, 为系统的频率增益因子或频率传输函数。
为系统的频率增益因子或频率传输函数。

例13.4.4 设线性时不变系统的输入x(t)与输出y(t)满足微分方程

其中a为已知正常数。
今输入过程是白噪声电压X(t),其自相关函数为 。求
。求
(1)输出电压过程Y(t)的自相关函数,以及X(t)与Y(t)的互相关函数。
(2)输出电压过程Y(t)的谱密度,以及X(t)与Y(t)的互谱密度。
解 先求系统的频率响应函数H(ω)和脉冲响应函数h(t)。
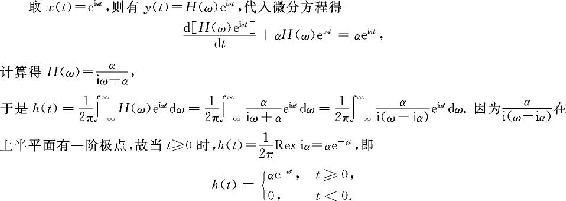


免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















