函数单调性

许多函数在一定的定义区间内呈现出单调性。微分中值定理为分析函数的单调性提供了非常有效的手段。

首先，由Lagrange定理，得到下述明显的结论。

定理4.2.1　假设f在［a,b］上连续，在（a,b）内可导。则f在［a,b］上单调增加（减少）的充分必要条件是：

f′（x）≥0　（f′（x）≤0），　x∈（a,b）．

特别地，f在［a,b］上为常数，当且仅当在（a,b）内f′（x）＝0．

证明　充分性可以通过Lagrange定理直接获证。实际上，如果f′（x）≥0，则对［a,b］上的任何两点x₁＜x₂，由Lagrange定理，存在ξ∈（x₁，x₂）使得

f（x₂）－f（x₁）＝f′（ξ）（x₂－x₁）≥0，

即f（x₂）≥f（x₁）．从而f在［a,b］上单调增加。

反之，若f在［a,b］上单调增加，则对任何x∈（a,b），

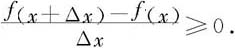
由导数定义和函数极限的性质知

从上述充分性证明中可得严格单调性的充分条件：f′恒正或恒负。

定理4.2.2　如果f在［a,b］上连续，在（a,b）内可导，f′在（a,b）内恒正（恒负），则f在［a,b］上严格单调增加（减少）。

我们将此证明留作习题。

当f在（a,b）内可导时，“f′在（a,b）内恒正或恒负”等价于“f′在（a,b）内没有零点”。这一等价性证明需要关于导函数的达布定理：导函数在区间上的值域也是区间。有兴趣的读者可参阅相关文献。然而根据Fermat定理，可以直接证明在上述定理中替换了这一等价性条件的相同结果。

定理4.2.3　设f在区间［a,b］上连续，在（a,b）内可导，且f′在（a,b）内没有零点，则f在［a,b］上严格单调。

证明　由于f′在（a,b）内没有零点，根据Fermat定理，f在区间［a,b］上的最小值、最大值只能在端点取到。不妨设f（a）为最小值，f（b）为最大值。从而当x∈（a,b）时，

f（a）＜f（x）＜f（b）．

如果f在［a,b］上非严格单调增加，那么在［a,b］内存在x₁＜x₂，使得f（x₁）≥f（x₂）．显然x₁≠a．注意到f（x₁）≥f（x₂）≥f（a），f在［a，x₂］上的最大值必可在（a，x₂）内取到。因而f在（a，x₂）内有一个极大值点ξ．根据Fermat定理，ξ必为f′的零点，从而得出矛盾。因此，f在［a,b］上必定严格单调增加。　　□

“f′没有零点”并不是严格单调的必要的条件。例如，f（x）＝x³严格单调，但其导函数却有一个零点。函数严格单调的充分必要条件，建立在关于导函数零点集的非区间性要求上。

定理4.2.4　假设f在［a,b］上连续，在（a,b）内可导。则f在［a,b］上严格单调增加的充分必要条件是：f′（x）≥0，且f′的任何部分零点都不能构成（非单点）区间。

必要性是显然的，可用反证法证明充分性。有兴趣的读者可尝试证明之。

例4.2.5　考虑函数f（x）＝（2x＋1）e^-x的单调性。

由于f′（x）＝（1－2x）e^-x，当x＞1/2时，f′（x）＜0；当x＜1/2时，f′（x）＞0．因此，f在（－∞，1/2］内严格单调增加，在［1/2，＋∞）内严格单调减小。

利用函数的单调性，可以简单地证明一些不等式。

例4.2.6　证明不等式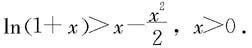

证明　考虑不等式两端的差函数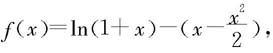x∈［0,＋∞）．我们只需证明：当x＞0时，f（x）＞0．为此考虑f在［0，∞）的单调性。由于在［0,＋∞）上f连续，在（0,＋∞）内f可导，且

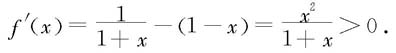
因此，f在［0,＋∞）严格单调递增，从而当x＞0时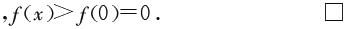

上述这种利用单调性证明不等式的方法，在证明其他一些不等式时，可能需要多次使用。例如在下述例子中我们需要在x＝0的两侧利用函数的单调性。

例4.2.7　证明在当x≠0时总有如下不等式：e^x＞1＋x．

证明　令f（x）＝e^x－（1＋x）．因为f′（x）＝e^x－1．显然，当x＜0时，f′（x）＜0；当x＞0时，f′（x）＞0．因此f在（－∞,0］上严格单调递减，在［0,＋∞）上严格单调递增。于是x≠0时，总有