一些特殊被积函数的不定积分

一、有理函数的不定积分

定义5.3.1　设两个实系数多项式P和Q没有共同的零点，其商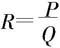称为有理函数。如果P的次数小于Q的次数，则称R为有理真分式；如果P的次数大于或等于Q的次数，则称R为有理假分式。

对有理假分式，可以通过做除法将其表示成一个多项式和一个有理真分式之和。例如对我们可以化为

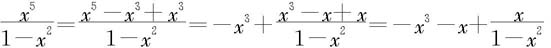
由于多项式的积分是容易求的，所以对有理函数的不定积分我们只须研究如何求有理真分式的不定积分。下面给出一个代数学定理，其证明过程可在复变函数课程中找到，这里从略。

定理5.3.2　设是一个有理真分式，则其分母Q有分解式

Q（x）＝q⁰（x－a）ⁱ…（x－b）^j（x²＋px＋q）^k…（x²＋sx＋t）^ι，

其中q⁰，a，…b，p，q，…，s，t为实数，且p²－4q＜0，…，s²－4t＜0，i，…，j，k，…ι为自然数，且R可表示成

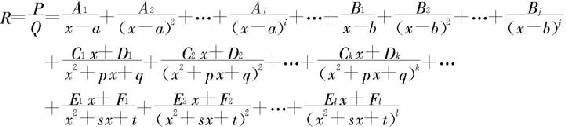
其中A₁，A₂，…，A_i；B₁，…，B_j；C₁，D₁，C₂，D₂，…，C_k，D_k；E₁，F₁，E₂，F₂，…，E_ι，F_ι都是唯一确定的实数。

定理5.3.2表明，有理真分式可以分解成下列两类分式（称之为部分分式）之和：

其中n为自然数。

因此，求有理函数的不定积分问题就归结为求以上两类部分分式的不定积分问题。当然，在求不定积分之前，需要将有理函数分解成多项式和有理真分式之和，将有理真分式分解成上述两类部分分式之和。

请看以下例题：

例5.3.3　将有理真分式分解为部分分式之和。

解　由定理5.3.2可设

消去分母得　x²－5＝A（x－2）²＋B（x＋1）（x－2）＋C（x＋1），

则　　x²－5＝（A＋B）x²＋（－4A－B＋C）x＋4A－2B＋C．

比较等式两边x的同次幂系数，有

解此方程组，得因此所求部分分式之和表示为

例5.3.4　分解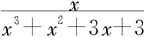为部分分式之和。

解　首先将分母分解因式得

x³＋x²＋3x＋3＝（x＋1）（x²＋3），

由定理5.3.2设

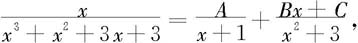
去分母得　　x＝A（x²＋3）＋（Bx＋C）（x＋1），

令x＝-1，代入得再代入上式整理得

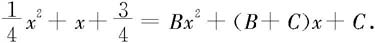
比较平方项和常数项的系数即得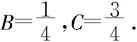

因此原有理式可分解为

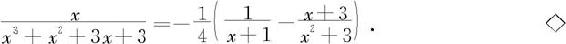
例5.3.5　分解为部分分式之和。

解　分母分解因式为x⁴－3x³＋3x²－x＝x（x－1）³，因此设

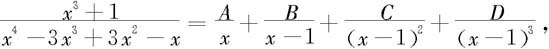
去分母之后可得

x³＋1＝A（x－1）³＋Bx（x－1）²＋Cx（x－1）＋Dx．

若将等式右边展开再合并同类项，再比较等式两边相同幂次的系数，自然可以解得待定系数A、B、C和D，但计算会比较烦一些。下面我们可以通过取x的不同特殊值来方便地得到待定系数的值：

令x＝0有　1＝-A，所以得A＝-1；

令x＝1有　2＝D，所以得D＝2；

令x＝-1和x＝2分别有解得B＝2，C＝1．

因此得分解式为

下面讨论上述两类部分分式的不定积分。

（一）对于第（1）类部分分式也就是求

当n＝1时，

当n＞1时，

（二）对于第（2）类部分分式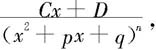（p²－4q＜0）：

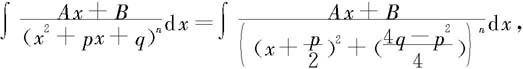
令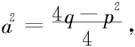作变量替换有

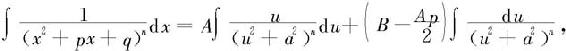
其中第一个不定积分为：

当n＝1时，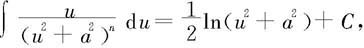

当n≥2时，

对第二个不定积分，记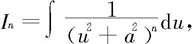由例5.2.11（3）知，可反复利用递推关系：

将所求不定积分归结为I₁的计算，而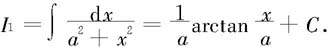

综上所述，有理函数的不定积分问题就完全解决了，且可得：一切有理函数的原函数可以用有理函数、对数函数及反正切函数表示出来。

例5.3.6　求不定积分

解　由例5.3.5知

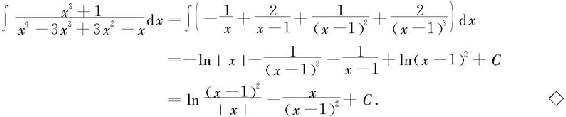
例5.3.7　求不定积分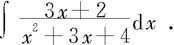

解　此不定积分当然可以按照前面所述步骤把它计算出来，但有时适当用点化简技巧可以使计算更加方便，如有

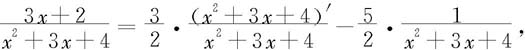
所以

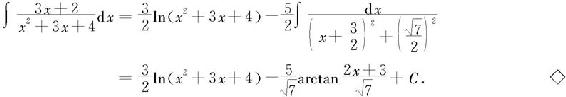
虽然有理函数的积分总可以通过将有理函数化成部分分式之和，再对每一个部分分式求不定积分的方法来解决，但此方法往往计算比较复杂，所以在计算时应尽量采用其他更为简便的方法，请看下面例题。

例5.3.8　求

解　若将被积函数分解成部分分式，形式上有10项之多。现作变量替换x－1＝t，有

例5.3.9　求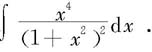

解　用分部积分法，得

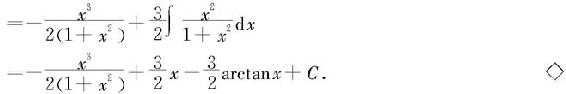
二、可有理化函数的不定积分

有些不定积分中的被积函数本身并不是有理函数，但通过适当的变量替换以后，可以将其化为关于新变量的有理函数不定积分，从而可以用前述方法计算出来。

（1）设R为有理函数，则以e^x为变量的有理函数R（e^x）的积分可通过变换量替换x＝lnt，化成有理函数的积分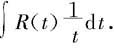

例5.3.10　求不定积分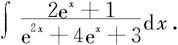

解　令x＝lnt（t＞0），即t＝e^x，则于是

代入原变量化简得

（2）三角有理函数的不定积分　我们称形如

的表达式为x和y的二元多项式，其中a_ij∈，i＝1，2，…，m；j＝1，2，…，n；称两个二元多项式的商为二元有理函数，记为R（x,y）；称R（sinx,cosx）为三角有理函数，例如均是三角有理函数。下面讨论计算不定积分

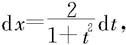设｜x｜＜π，即x＝2arctant，则由三角恒等式可得以下公式

所以有

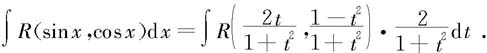
这就将原三角有理函数的不定积分化成了有理函数的不定积分，而有理函数的不定积分我们已经解决了，因此，变量替换或x＝2arctant被称作“万能变换”。

例5.3.11　求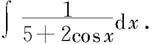

解　作变量替换有

由于有理函数的不定积分计算一般比较复杂，所以在计算中也尽量灵活运用其他方法，具体情况具体分析，以便避开繁琐复杂的计算。

例5.3.12　求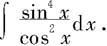

解　因为

对于一些特殊情形的三角函数，我们可采取特殊的方法来计算其不定积分，下面例子中所采用的方法具有一般的意义，请读者细心体会。

例5.3.13　求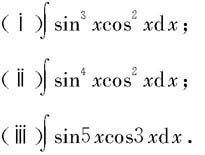

解

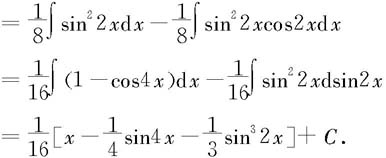
（3）某些无理函数的不定积分　对无理函数的不定积分，有些是可以通过简单的“处理”就能得到解决，有些则要通过一定的变量替换来进行有理化。

例5.3.14　求

解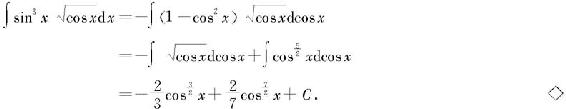

例5.3.15　求

解　作变量替换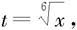即x＝t⁶，dx＝6t⁵dt，代入得

下面我们指出，对形如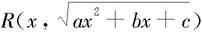和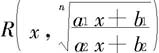的函数，是可以有理化的，前者可通过配方将根号化作形如的函数（其中k为常数），再作三角变量替换便可有理化；对于后者，设a₁b₂≠b₁a₂，否则根号里面是一个常数，就不需要有理化了，作变量替换这样原不定积分就化成关于t的有理函数的积分。

例5.3.16　求

解　因为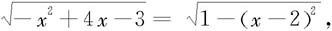作变量替换x－2＝sint，于是

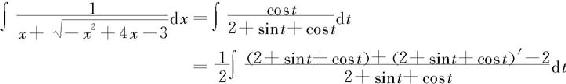
又因为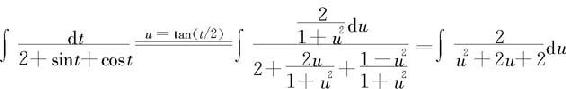

所以

例5.3.17　求a＜x＜b．

解法一　作变量替换则

而

因此

解法二　因为有恒等式再考虑到被积函数有根号，所以作变量替换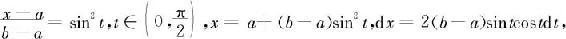：于是有

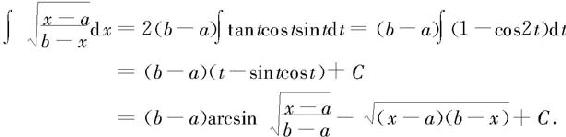
还有许多类型的函数，可以化作有理函数来求不定积分，但处理的方法不尽相同，这里不一一介绍了。

一般，对于一个不定积分，可能会有很多处理方法将其计算出来，但最基本的计算不定积分的方法还是换元法（包括凑微分方法）与分部积分法。当然，要熟练掌握求不定积分的技巧，就要通过不断练习，培养自己分析不同的被积函数，找出相应的处理办法的能力。

这里还需指出，对于某些不定积分，例如：和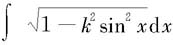（0＜k＜1）等等，他们的被积函数虽然是初等函数，但他们的原函数却不是初等函数，在第7章中我们将用其他形式来表示这些函数的原函数。