§6.4 定积分的换元法和分部积分法
有了Newton-Leibniz公式,计算定积分的问题便化成了求原函数(不定积分)的问题,而求不定积分在上一章我们介绍了换元法和分部积分法两种基本方法,所以求定积分也相应地有这两种方法。
定积分的换元法
首先我们讨论求定积分的换元法。
定理6.4.1 设函数f在区间I上连续,且a,b∈I,函数φ在[α,β]上有连续的导函数,当φ([α,β])⊂I,且φ(α)=a,φ(β)=b,则
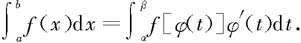
证明 由f的连续性知存在原函数,设F为f在[a,b]上的一个原函数,有

又因为
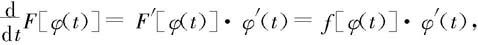
由Newton-Leibniz公式得

所以
在定理6.4.1中,事实上就是通过变量替换x=φ(t),将定积分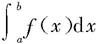 计算化成了定积分
计算化成了定积分 的计算,从而简化计算求出其值。与不定积分变量替换法对照比较,这里进行变量替换时除了要考虑函数φ的条件外,还要对积分的上、下限进行相应的替换,但另一方面就不必像不定积分的变量替换法那样“代回原变量”了。
的计算,从而简化计算求出其值。与不定积分变量替换法对照比较,这里进行变量替换时除了要考虑函数φ的条件外,还要对积分的上、下限进行相应的替换,但另一方面就不必像不定积分的变量替换法那样“代回原变量”了。
例6.4.2 求
解 作变量替换x=t2,则dx=2tdt,当t=1时x=1;当t=3时x=9,由定理6.4.1有

注 在例6.4.2中对于变换x=t2,因为当t=-1时x=1,当t=3时x=9,那么变换后的积分区间可取为[-1,3],这时也满足定理6.4.1的条件,请读者按此变量替换进行计算。
例6.4.3 求
解 作变量替换x=asint,当t=0时x=0,当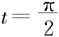 时x=a,dx=acostdt,所以
时x=a,dx=acostdt,所以
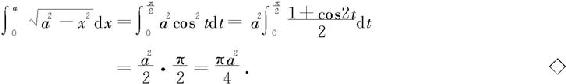
例6.4.4 设函数f在区间[-a,a]上可积,则有

证明  对右边第一个积分作变量替换x=-t得
对右边第一个积分作变量替换x=-t得
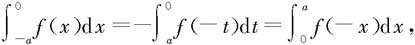
所以
从例6.4.4可得:
(1)若f是区间[-a,a]上的奇函数且可积,则有
(2)若f是区间[-a,a]上的偶函数且可积,则有
例6.4.5 设f是以T为周期的可积周期函数,则有
 其中a为任意常数.
其中a为任意常数.
证明 因为

对等式右边第三个积分,作变量替换x=t+T,并由对 x,f(x+T)=f(x)得
x,f(x+T)=f(x)得

因此有

例6.4.5说明了周期函数在任一周期内的定积分值相等。
例6.4.6 设函数f在[0,1]上连续,证明

并计算定积分
证明 作变量替换x=π-t,则有
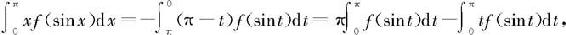
移项整理即得
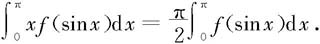
于是有
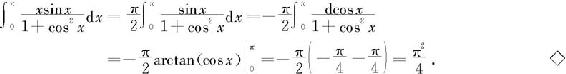
例6.4.7 设函数f连续, 求F′(x).
求F′(x).
解 作变量替换u=x-t,有

由微积分第一基本定理得

定积分的分部积分法
对在区间[a,b]上具有连续导数的函数u,v,由
udv=d(uv)+vdu,
两边从x=a到x=b积分得

或 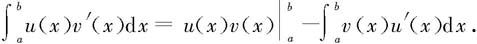
这就是定积分的分部积分公式。从中也可以看出,定积分的分部积分公式在计算过程中是一边计算一边“及时”地在化简,而若先用不定积分的分部积分公式求出原函数后再将上下限代入求值,则往往会繁杂得多。
例6.4.8 计算
解
例6.4.9 求
解 记 作变量替换
作变量替换 得
得
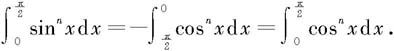
由分部积分公式有
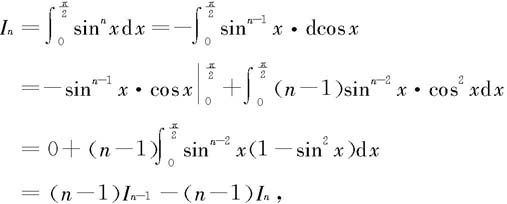
得递推公式
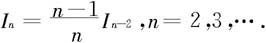
因此,当n为偶数时,有

当n为奇数时,有
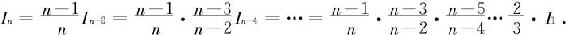
而 于是得
于是得

例6.4.10 求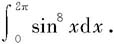
解 由例6.4.4和例6.4.5可知

再由例6.4.9得
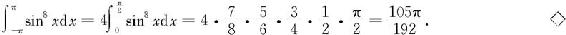
例6.4.11 设 求
求
解 用分部积分法得

又因为F(-1)=0,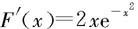 所以
所以
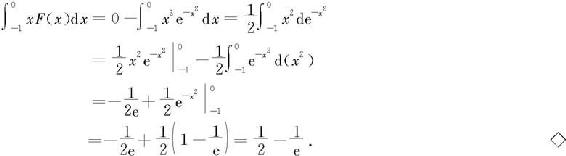
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















