根据定积分的思想，利用定积分的定义及其计算方法，我们可以解决一些几何和物理上的具体问题，请读者注意体会下面各应用问题的分析过程和处理方法。
定积分在几何上的应用
定积分在几何上的应用我们主要介绍曲线围成的平面图形的面积、平面上曲线段的长度（曲线弧长）、旋转体的体积及其侧面积等。
一、曲线围成的平面图形的面积
设函数f，g在［a,b］上连续，且对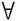
x∈［a,b］有f（x）≥g（x），则由定积分的定义知曲线y＝f（x），y＝g（x）及直线x＝a，x＝b围成的平面图形（如图6.6）面积为
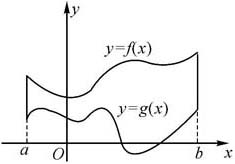
图6.6
例6.5.1 求由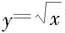
和直线y＝x围成的图形面积。
解 如图6.7所示，两曲线的交点为
O（0,0）与M（1,1）
所求面积为
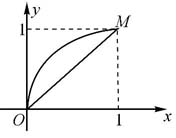
图6.7
例6.5.2 求x＝4－y2和x－2y－1＝0围成的平面图形面积。
解法一 曲线x＝4－y2和x－2y－1＝0的交点为M（3,1）和N（-5,-3），如图6.8所示。
因此，所求面积为
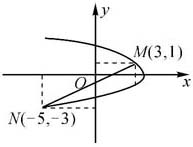
图6.8
解法二 现将y作为积分变量（自变量），即把［-3,1］作为积分区间，则由定积分的定义同理可得所求面积为
从例6.5.2可以看出，在直角坐标系中用定积分计算平面图形面积时，可对图形进行“x方向”的分割，也可以对图形在“y方向”进行分割，选择适当的分割（积分变量或积分区间），可使得计算简单方便。
下面我们介绍在极坐标系下利用定积分计算平面图形面积的方法。
首先考察曲线r＝r（θ）与半射线θ＝α，θ＝β所围图形（图6.9）的面积：
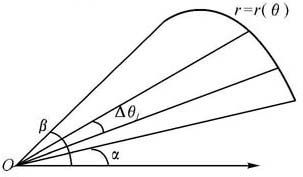
图6.9
设P＝［α＝θ0,θ1,…,θn＝β］是［α,β］的一个分割，ξ＝［ξ1,ξ2,…,ξn］是P的介点，这就将图形分成了n个小块，记∆θi＝θi－θi－1，则第i（i＝1,2,…,n）小块的面积近似为一个扇形面积
∆θi，所以，所求面积近似为
因此所求面积可表示为
例6.5.3 分别求：（1）心形线r＝a（1＋cosθ）；（2）双纽线（x2＋y2）2＝x2－y2围成的图形面积。
解 （1）如图6.10所示，心形线关于极轴对称，所以心形线围成的图形面积为
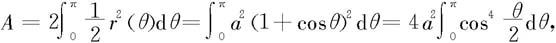
作变量替换
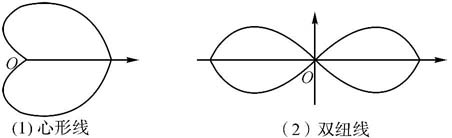
图6.10
（2）将双纽线方程改写成极坐标方程为
r2＝cos2θ，
由对称性（如图6.10）可知
从上例可见，求对于像心形线和双纽线这样的曲线所围成的面积用极坐标计算很方便，但若用直角坐标系计算会比较复杂。
二、平面曲线的弧长
在平面中，一条直线段的长度可以用两端点之间的距离来计算，圆周的长度可以通过求其内接或外切正多边形周长的极限来得到，对一般的光滑曲线段的长度（称之为弧长），我们可以利用定积分的方法来计算。
定义6.5.4 设f∶［a,b］→
，图形C＝｛（x,y）∈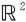
｜y＝f（x）,x∈［a,b］｝为一平面曲线。
（1）若f连续，则称图形C为连续曲线；（2）若f连续可导，则称图形C为光滑曲线。
下面我们来求曲线C＝｛（x,y）∈
｜y＝f（x）,x∈［a,b］｝的弧长：设
P＝［a＝x0,x1,…，xn－1，xn＝b］
是［a,b］的一个分割，则Qi＝（xi，f（xi））∈C，i＝0，1，2，…，n．而直线段QiQi＋1的长度可近似作为Qi，Qi＋1之间的曲线弧长，也就是
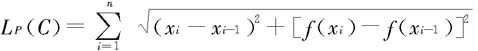
可近似作为所求曲线C的弧长，如图6.11所示。
图6.11
如果极限
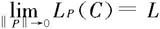
存在，则L即为C的长度，并称C是可求长的曲线。
当C为光滑曲线时，由Lagrange中值定理知存在ξi∈（xi－1，xi）使
f（xi）－f（xi－1）＝f′（ξi）（xi－xi－1）
所以ξ＝［ξ1,ξ2,…,ξn］为P的一个介点，因此有
因为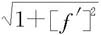
在［a,b］上连续，所以在［a,b］上可积，于是由定积分定义得
例6.5.5 求悬链线
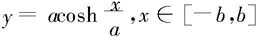
的曲线弧长。
解 所求弧长为
这里
分别为双曲余弦函数和双曲正弦函数。 ◇
若曲线C由参数方程
给出，这里函数φ及ψ在区间［α,β］上具有连续的且不同时为零的导数，又端点对应值t＝α和t＝β，则可证明曲线C是可求长的，且其弧长计算公式为
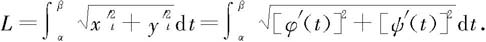
读者可自己试着完成证明。
例6.5.6 求摆线x＝a（t－sint），y＝a（1－cost）（0≤t≤2π）一拱的弧长．
解 所求弧长为
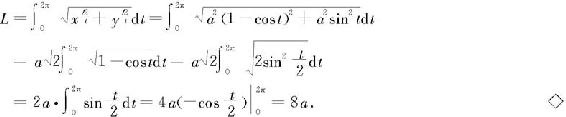
若曲线C是由极坐标方程
r＝r（θ），θ1≤θ≤θ2
给出的，且r（θ）在［θ1，θ2］上有连续的导数，这时可取θ作参数，参数方程可写为
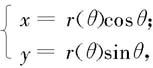
于是得极坐标下的弧长计算公式
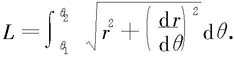
例6.5.7 求Archimedes（阿基米德）螺线r＝eaθ，0≤θ≤2π，a＞0的弧长。
解 由极坐标弧长的计算公式得所求弧长为
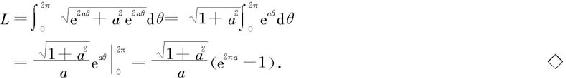
三、旋转体体积和侧面积
对圆柱、圆锥和圆台等规则立体的体积和侧面积，我们可用古典的方法进行计算，但对一些不规则的立体，就不那么容易了。下面我们对一些特殊类型的不规则立体用定积分来计算它们的体积和侧面积。
设立体介于x＝a和x＝b之间，如图6.12所示，其垂直于x轴的截面面积A（x）是x的连续函数，现求此立体体积V：
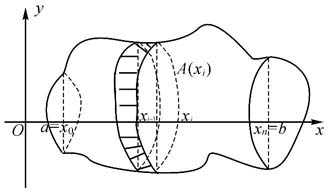
图6.12
区间［a,b］的任一分割P＝［a＝x0,x1,…,xn－1,xn＝b］将立体分为n个薄片，当‖P‖很小时，小区间［xi－1，xi］上的薄片可近似看为柱体，所以其体积近似为
A（xi）（xi－xi－1），i＝1，2，…，n．
于是所求体积
又因为A（x）在［a,b］上连续，所以由定积分的定义得
由此公式知，如果我们知道了立体在［a,b］上截面面积表达式A（x），则体积可用其定积分求得。另外也表明，如果两个立体在其每一点的截面面积相同，则它们的体积相同，这即为我国古代数学家祖冲之的观点：幂势既同则积不容异。
例6.5.8 设有半径为a的圆柱体，用与底面交成α角，且过底圆直径AB的平面所截，试求截下的楔形体积。
解 如图6.13所示，则底圆方程为
x2＋y2＝a2，
垂直于x轴的截面都是直角三角形，任一x∈［-a,a］处的直角三角形的面积为
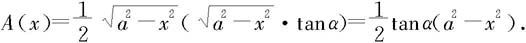
因此所求楔形的体积是
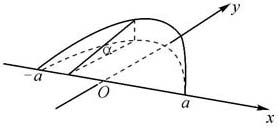
图6.13
旋转体的体积
设立体是由非负连续曲线y＝f（x）和直线x＝a，x＝b及x轴围成的平面图形绕x轴旋转一周而成的旋转体（如图6.14），这时每一处x∈［a,b］的截面就是以f（x）为半径的圆，因而截面面积为
A（x）＝πf2（x），
所得旋转体体积公式
图6.14
例6.5.9 设D是由抛物线
与直线x＝2及x轴围成的图形，试求D分别绕x轴和y轴旋转而成的旋转体体积Vx和Vy。
解 如图6.15所示，D绕x轴旋转而成的旋转体体积为
D绕y轴旋转而成的旋转体体积为
图6.15
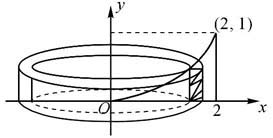
图6.16
在求Vy时，我们也可以采用以下方法：设P＝［0＝x0,x1,…,xn－1,xn＝2］为区间［0,2］的一个分割，将区间［0,2］分割成n个小区间，所求旋转体体积可以用n个以y轴为轴线的同心圆筒体积的和来近似，如图6.16．若ξ＝［ξ1,ξ2,…,ξn］是P的介点，则第i个小区间上的圆筒的体积近似为2πξi·
所以所求旋转体体积近似为
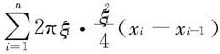
由定积分定义可知，绕y轴旋转而成的旋转体体积为
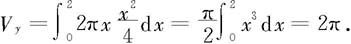
这种用n个“套筒”体积来近似旋转体体积的方法，我们可形象地称之为套筒法，有时在计算上会带来方便。 ◇
旋转曲面侧面积
设f是区间［a,b］上具有连续导函数的非负函数，现在求由曲线y＝f（x）（a≤x≤b）绕x轴旋转一周而成的旋转曲面的侧面积S，如图6.17．
对于区间［a,b］的任一分割
P＝［a＝x0,x1,…,xn－1,xn＝b］，
Qi＝（xi，f（xi）），i＝0，1，2，…，n在曲线y＝f（x）（a≤x≤b）上，而直线段QiQi＋1绕x轴旋转一周而成的圆台面的侧面积
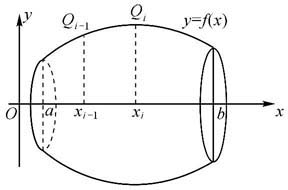
图6.17
可近似作为Qi，Qi＋1之间的曲线弧长绕x轴旋转一周而成的旋转体的侧面积，由Lagrange中值定理知存在ξi∈（xi－1，xi）使
f（xi）－f（xi－1）＝f′（ξi）（xi－xi－1）
因此有
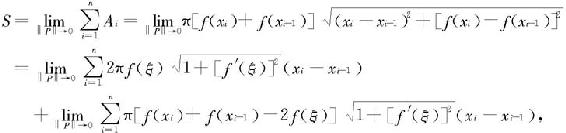
由f在［a,b］上的一致连续性可证明
于是再由f，f′在［a,b］上的连续性及定积分定义可知
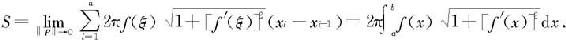
这里需要指出的是，上述推导过程中，旋转体在［xi－1，xi］部分的侧面积不能用以半径为f（ξi）（ξi∈［xi－1，xi］），高为xi－xi－1的圆柱的侧面积来近似，因为这时的误差之和当‖P‖→0时不是一个无穷小量，即极限不等于零。
例6.5.10 求半径为R的球面积。
解 球面可以看成为上半圆弧
（-R≤x≤R）绕x轴旋转一周而成的旋转曲面，所以其面积为
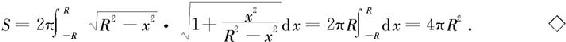
同理容易得到，若曲线由参数方程
给出，函数φ及ψ在区间［α,β］上具有连续的且不同时为零的导数，且ψ（t）≥0，则其绕x轴旋转一周而成的旋转曲面的侧面积为
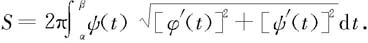
例6.5.11 求摆线
（0≤t≤2π）绕x轴旋转一周所得旋转曲面侧面积。
解 由上面的侧面积公式，所求侧面积为
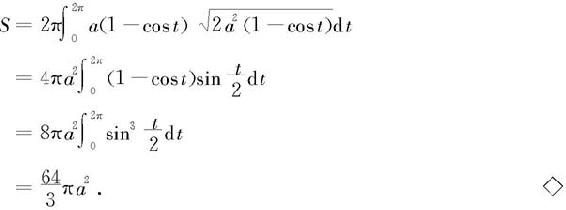
定积分在物理上的应用
在前面介绍的定积分在几何上应用中，主要方法是首先确定一个积分区间和积分变量，然后对此区间的任一分割，在小区间上写出所求量的近似值表达式（称之为微元），最后写出Riemann和以及相应的定积分表达式，从而计算得所求结果。上述方法最重要的是如何写出小区间上的微元，所以此计算方法也称为微元法。下面我们将用微元法来计算一些物理问题，也就是用定积分来解决一些物理问题。
一、液体的侧压力
物体浸在液体中，其表面所受压力与各点的压强有关，而液体中的压强与液体的深度成正比，因而物体在液体中所受的静压力是液体深度的函数，而且同一深度处的压强相等。
例6.5.12 半径为2米的圆形薄片垂直放置水中，圆心离水面6米，求薄片受到的水压力。
解 取坐标系如图6.18所示，用平行于x轴的直线将圆形薄片分割成一条条窄带，也就是将积分变量y的积分区间［-2,2］进行分割，在小区间［y，y＋∆y］上，窄带的面积近似为
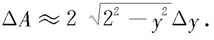
又因为
压力＝压强×受力面积。
而窄带上每处的压强可以近似看成是相同的，于是窄带上所受的水压力近似为
其中ω＝1000（千克／米3）为水的比重。∆F即为所求压力的微元，因此有
图6.18
二、变力做功
例6.5.13 设有一直径为8米的半球形水池，欲将满池的水全部抽到距池口高10米的水箱上，问至少该做多少功？
解 选取坐标系如图6.19所示，这时水池口圆的方程为
x2＋y2＝16．
因为 功＝力×位移，
这里的力是水的重力，位移是各处水抽到水箱口的高度差，因为同一水层到水箱口的距离是一样的，于是将池水水平分割成“小薄圆片”，现考察位于区间［x，x＋∆x］⊂［0,4］上一层水抽到水箱口所需的功，得功的微元为
∆W≈ωgπy2·∆x·（x＋10）＝ωgπ（x＋10）（16－x2）∆x，
其中水的密度ω＝1000（千克／米3），所以所求之功为
图6.19
三、密度不均匀物体的质量问题
例6.5.14 一长为10米的细杆，其线密度为ρ＝2x＋3（千克／米），其中x为点到细杆一端的距离，求细杆的质量。
解 取细杆的一端为坐标原点，如图6.20，沿x轴方向将细杆分割成若干小段，则位于小区间［x，x＋∆x］⊂［0,10］的一小段质量微元为
∆M≈ρ∆x＝（2x＋3）∆x，
因此所求质量为
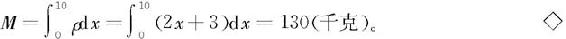
图6.20
例6.5.15 设有一半径为R的半圆形薄板，其面密度分布是点到圆心距离r的函数ρ（r）＝a＋br，试求此薄板的质量。
解 薄板每一处的密度是其到圆心的距离r的函数，所以在薄板内的小圆上各点密度相同，因此用同心圆将半圆薄板分割成若干个半圆环，如图6.21，考察位于小区间［r，r＋∆r］⊂［0,R］上的半圆环的质量，得质量微元为
∆M≈ρ（r）·πr∆r＝π（a＋br）r∆r，
于是所求质量为
图6.21
四、物体间的万有引力问题
例6.5.16 设有一长度为ι，质量为M的匀质细杆，在其中垂线上距细杆为h处有一质量为m的质点，试求细杆对质点的引力。
解 取细杆的中点为坐标原点，且质点落在y轴正向上，如图6.22所示。将细杆分割成若干小段，则位于小区间［x，x＋∆x］⊂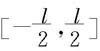
上小段细杆（质量为
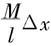）对质点的引力大小为
其中K为万有引力常数，这引力的方向是从质点指向这一小段处。因为引力是矢量，所以我们将每一小段的引力分别分解到x轴方向和y轴方向上，然后分别相加。又从细杆与质点的位置的对称性可知，x轴方向分力相互抵消合力为零，所以只需计算y轴方向的分力，因此可得所求引力的微元为
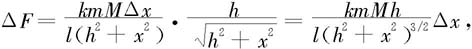
于是所求细杆对质点的引力大小为
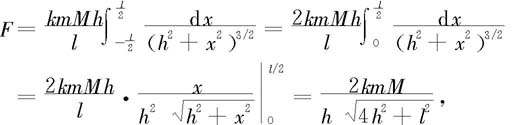
引力方向为沿y轴负向。 ◇
图6.22
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
