§7.6 幂级数的应用
函数值的近似计算
运用幂级数展开可以近似计算许多初等函数在某点的近似函数值,如三角函数、根式函数、对数函数等,而且利用余项Rn(x)可以估计出近似值的误差。以下举几个例子。
例7.6.1 计算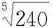 的近似值,要求误差不超过0.0001。
的近似值,要求误差不超过0.0001。
解 因为
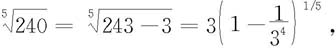
所以在二项展开式中取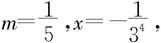 即得
即得
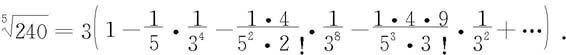
这个级数收敛很快,取前两项的和作为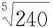 的近似值,其误差(也叫截断误差)为
的近似值,其误差(也叫截断误差)为
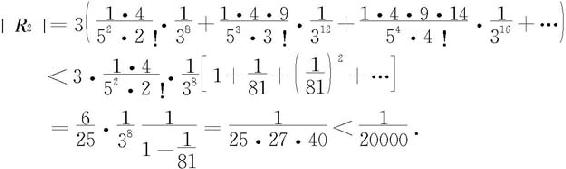
于是取近似值为
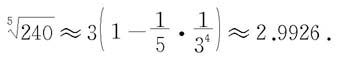
例7.6.2 计算ln2的近似值,要求误差不超过0.0001.
解 在上节例7.5.6中,令x=1可得

如果取这级数前n项的和作为ln2的近似值,其误差为
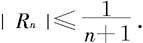
为了保证误差不超过10-4,需要取级数的前10000项进行计算。这样做计算量太大了,我们必须用收敛较快的级数来代替它。
把展开式
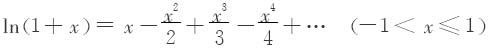
把x换成-x,得
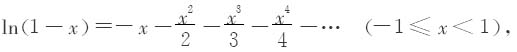
两式相减,得到不含有偶次幂的展开式:
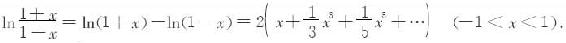
令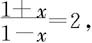 解出
解出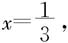 以
以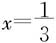 代入最后一个展开式,得
代入最后一个展开式,得
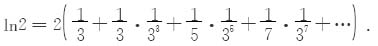
如果取前四项和作为ln2的近似值,则误差为
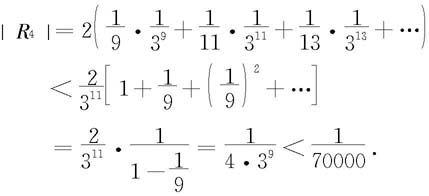
于是取 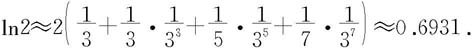
积分的近似计算
利用幂级数不仅可以计算一些函数值的近似值,而且可以计算一些定积分的近似值。具体地说,如果被积函数在积分区间上能展开成幂级数,则把这个幂级数逐项积分,用积分后的级数就可算出定积分的近似值。
例7.6.3 计算定积分
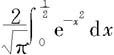
近似值,要求误差不超过0.0001(取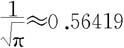 ).
).
解 将ex的幂级数展开式中的x换成-x2,就得到被积函数的幂级数展开式
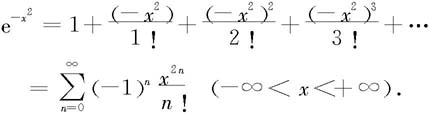
于是,根据幂级数在收敛区间内逐项可积性,得
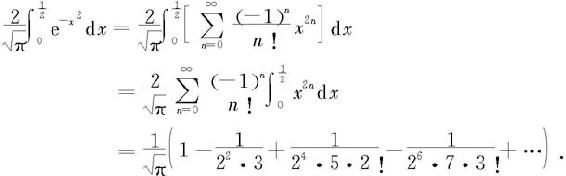
取前四项的和作为近似值,其误差为
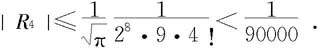
所以

例7.6.4 计算积分
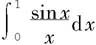
的近似值,要求误差不超过0.0001.
解 由于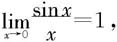 因此所给积分不是广义积分。如果定义被积函数在x=0处的值为1,则它在积分区间[0,1]上连续。
因此所给积分不是广义积分。如果定义被积函数在x=0处的值为1,则它在积分区间[0,1]上连续。
展开被积函数,有
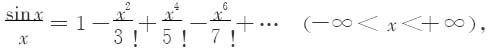
在区间[0,1]上逐项积分,得
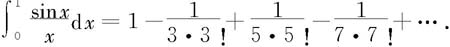
因为第四项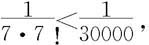 所以取前三项的和作为积分的近似值:
所以取前三项的和作为积分的近似值:
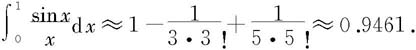
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















