古代人怎样记数

古代人怎样记数

现在我们已经知道了记数需要符号和进位的基数，那么自然就会想到在记数制还没有统一之前不同的民族和不同的地区会有不同的记数法。这些不同表现在数码的不同和进位基数以及是否是位值制的不同上。古代人的记数方法有多种，我们在这里介绍几种。

埃及象形文字记数法

古埃及有4种文字，最古老的是象形文字，大约在公元前3000年就已形成。象形文字记数法进位的基数是10，但不是位值制。因此采用简单累加制，即书面上的数是各个符号所代表的数之和。1就是竖着的一短划，10像拱门，100是一卷绳，1000像荷花，10000是一个指头。有时向左弯，有时向右弯，100000有好几种写法，有时像蝌蚪或鱼，有时像小鸟。如:

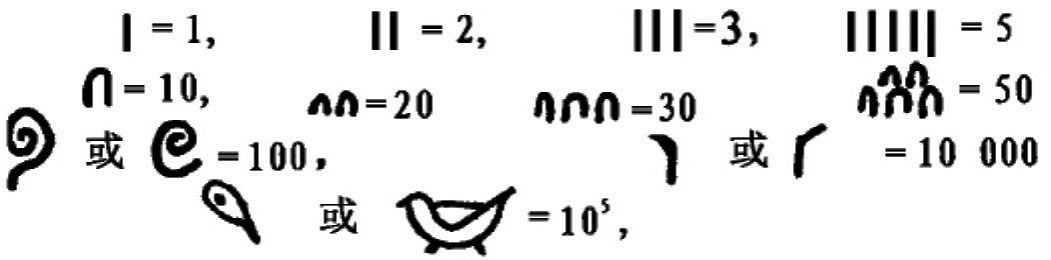
这种记数法每一个较高的单位(10的乘幂)都要创设一个新符号，记数时有多少单位就要重复多少次，上下左右书写均可，但符号毕竟是有限的，记太大的数就有困难了。

罗马记数制

这是5进的记数制，也不是位值制。12世纪以前盛行于欧洲，现在在某些场合下还在使用，如书本的卷数、章节的序号、正文前的页码等。用拉丁大写字母表示数目(有时也用小写):

一个简单的数要写成长长的一串，如4855= MMMMDCCCLV，从左到右书写，单位按从大到小排列。但如果较小单位写在较大单位之左，要用“减法原则”，如:Ⅳ=4=5－1，Ⅸ=9=10－1，Ⅵ=6=5+1等。

罗马记数法是相当笨拙的，这使得算术四则运算非常复杂。

巴比伦楔形文字记数制

亚洲西部的底格里斯河与幼发拉底河之间的地带，通常叫做两河流域，它和尼罗河流域一样，也是人类早期文明的发祥地之一。这块地域古代叫做美索不达米亚。最早居住在这里的民族有苏美尔人和阿卡德人。公元前19世纪，这里建立了巴比伦王国。这个地区曾广泛使用一种楔形文字，先用削尖的木笔在软泥板上刻写，然后烧干或晒干，使它坚硬如石，这些泥板被埋在地下数千年，经久不坏。19世纪上半叶考古学家在美索不达尼亚挖掘出大约50万块有文字的泥板，其中有300块被鉴定为数学泥板。这些泥板上载有数字表和一些数学问题。现在关于巴比伦的数学知识就来源于这些泥板。

大约在公元前1800—前1600年间，巴比伦人就使用了六十进制记数法。对于小于六十进制的整数，使用1(ㄚ)和10()两种符号来表示。

如25=2×10+5表示为

大于60的数，用位值制记数法，也是用上面两种记号来表示，如524551=2×60³+25×60²+42×60+31表示为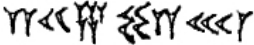

这里的ㄚ和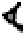都可以表示60的各次幂，因为没有零号，这种记数法是不完善的。以60为基数的位值制应该是将数写成a_n·60ⁿ+a_n－1·60^n－1+…+a₂·60²+a1·60+a₀的形式，a_i(i=0，2，…，n)是60种不同符号中的某一个，这样，就需要60个符号。巴比伦人的记数法只有两个符号，但他们不是二进制，是六十进制，60以下的数是用简单累加表示的。

玛雅记数制

玛雅人的数学，从仅存的资料中得知其包含:数的系统、位值制、零，以及使人印象深刻的记载时间的方法。不幸的是，对于大多数玛雅资料人们至今无法解读。例如，我们知道他们是按二十进制计算的，但我们没有他们利用这种系统计算日期的直接证据^[2]，因为有关日期的记录都被毁了。目前可以信赖的只有他们关于天文和历法的记载，从中知道他们发展了一种位值制系统，用它可以表示很大的数(实际上要多大都可以)。他们也用一个符号表示一个单位的空缺，因而可以说已经有了零的概念。这种符号像半开的眼睛，也像一只贝壳。由于宗教和仪式在他们的生活中占据了重要的角色，甚至控制了他们的生活，因而天文和日历的记录较为广泛。

玛雅人的数的系统多半受他们历法的影响。因为他们用的是一种修改的二十进制位值制体系:

但他们的位值制并不严格遵循二十进制，即不是1=20⁰，20=20¹，400=20²，8000=20³，160000=20⁴，…，而是越过头两位，从第三位起遵循二十进制。即

1=20⁰，20=20¹，360=18×20¹，7200=18×20²，14 000=18×20³，…

这里我们要注意的是，所用的18和20正是在他们的日历中提到的。玛雅人用一个符号代表零，这个零有两种作用:一是作为位置的持有者，二是作为数量。^[3]

中国筹算记数制

从流传至今的文献记载来看，最晚从春秋末期起，一直到元代末年，这一历史时期中国数学的主要计算工具是算筹。^[4]算筹是一般的称呼，还有其他的叫法，如策、筹、算、筹策、算子、筹算等多种。它是像筷子那样的小棍状物，大多用竹子制作，也有铁、骨头等质料的。用它摆出数字，就能进行计算。以算筹为工具进行的数学运算，称为筹算。它与算筹有同样悠久的历史。

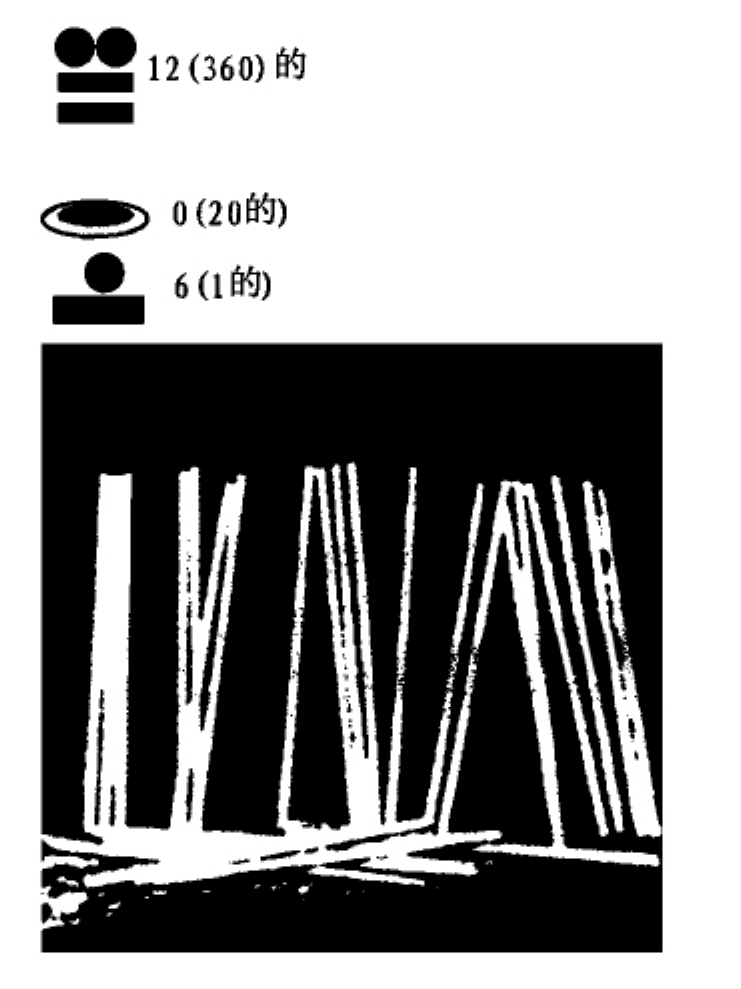
中国古代的计算工具——算筹

相应的记数制叫筹算记数制。筹算记数制是接近现代位值制的十进位值制。有纵横两种方式:

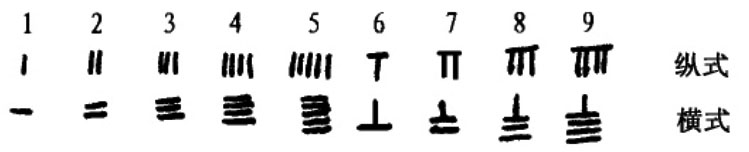
记数时个位常用纵式，其余纵横相间，如

空一格表示零，如

由于纵横相间，还有个位必定是纵式，所以空位不致看错。除了数码形式不同之外，和现在的十进位值制并无两样。这是当时世界上最简便的计算工具、最先进的记数制度，比古巴比伦的六十进位值制方便，比古埃及的十进位非位值制先进。中国古代数学有着辉煌的成就，这些成就大都借助于算筹与筹算取得的。

印度－阿拉伯记数制

从以上叙述可以看出，在数学史上，许多国家和民族发明了各种不同的数字符号(数码)和记数法。随着历史的前进，其中多数数码现已废弃不用，有些只在一定范围内和某些场合使用。当今国际上通用的数码就是我们熟知的阿拉伯数码。确切地说，应称作印度－阿拉伯数码。这种数字记号的演变和流传，有一段漫长而曲折的历史。

印度最早的数字记号可以追溯到婆罗米文字，它形成于公元前7—前8世纪。目前在寺庙的墙壁、石碑及铜片上发现的公元前3世纪时的数字写成下列形状:

图3－1　公元3世纪的印度数码

当时还没有零的记号，也没有采用位置记数法。以后渐渐向位值制发展，大约在公元600年已过渡到位值制记数法。最初用空一格表示零，后来用小点表示。而且，印度人对零的最大贡献是承认它是一个数，而不仅仅是空位或是一无所有。这种看法在3世纪时已经出现。^[5]到公元9世纪时，印度数码演变成:

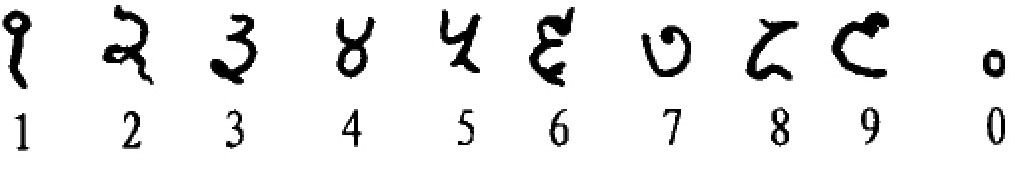
图3－2　9世纪的印度数码

公元773年，一位印度学者把印度的天文学著作带到阿拉伯的宫廷，后来被译成阿拉伯文。这样，印度数码开始传入阿拉伯国家。12世纪起，欧洲人开始将大量阿拉伯文的数学著作编译成拉丁文。意大利数学家斐波那契(1170—1250年)于1202年完成名作《算盘书》。开篇就介绍说，9个印度数码是9、8、7、6、5、4、3、2、1以及用这9个数码和记号0就可以写出任何数目。接下来的几章解释了位值制原理和计算方法。该书问世后广为流传，为印度－阿拉伯数码在欧洲的传播起了重要作用。因此，印度数码是通过阿拉伯国家和阿拉伯文传入欧洲的，在欧洲人的印象中，这些数码来自阿拉伯国家，所以称之为阿拉伯数码，这个名称一直沿用至今。

在我国，印度－阿拉伯数码最早于1892年出现在由美国传教士狄考文和邹立文合译的《笔算数学》中^[6]，不过当时的数目字是竖排的。后来由于封建保守思想的束缚，曾一度改回用汉字“一、二、三、…”。直到辛亥革命后，印度－阿拉伯数码才在我国正式通行。