阿基米得群牛问题

佩尔方程有着悠久而迷人的历史，它最早可上溯到公元前3世纪时的阿基米得群牛问题。关于这个问题的由来，有一种有趣的传说。

根据传说，公元前3世纪时，古希腊数学家阿波罗尼奥斯找到一个圆周率的近似值，比阿基米得的结果还要准确。而且，他还写了一篇讨论大数目字乘积的文章，并在文中批评阿基米得的工作。对此很生气的阿基米得为了报复，就设计了这个必须运算极大数字才能找到答案的群牛问题，并把它写在一封信中，寄给好友亚历山大城图书馆馆长埃拉托塞尼（以测量地球周长而闻名），以此向当时亚历山大的学者们挑战。

1773年，德国著名剧作家莱辛发现了一份记载有阿基米得群牛问题的手稿，问题以一首诗的形式叙述，整首诗由22组对偶句、44行诗句组成。

朋友，如果你自认为还有几分聪明，

请来准确无误地算一算太阳神的牛群，

它们聚集在西西里岛，

分成四群悠闲地品尝青草。

第一群像乳汁一般白洁，

第二群闪耀着乌黑的光泽。

第三群棕黄，第四群毛色花俏，

每群牛有公有母、有多有少。

先告诉你各群的公牛比例：

白牛数等于棕牛数再加上

黑牛数的三分之一又二分之一。

此外，黑牛数为花牛数的四分之一

加五分之一，再加上全部棕公牛。

朋友，你还必须牢记

花牛数是白牛的六分之一又七分之一

再搭上全部的棕色公牛。

但是，各群的母牛都有不同的比例：

白色的母牛数等于

全部黑色公母牛的三分之一又四分之一。

而黑母牛又是全部花牛的

四分之一加上五分之一，

请注意，母牛公牛都要算进去。

同样的，花母牛的数字

是全部棕牛的五分之一加六分之一。

最后，棕色母牛与全部白牛的

六分之一加七分之一相一致。

朋友，若你能确切地告诉我

这些公牛母牛膘肥体壮、毛色各异，

一共有多少聚集在那里，

你就不愧为精通算计。

但你还称不上聪明无比，

除非你能回答如下的问题：

把所有的黑白公牛齐集一起，

恰排成正方形，整整齐齐。

辽阔的西西里岛草地，

还有不少公牛在聚集。

当棕色的公牛与花公牛走到一起，

排成一个三角形状。

棕色公牛、花公牛头头在场，

其他的牛没有一头敢往里闯。

朋友，你若能够根据上述条件，

准确说出各种牛的数量，

那你就是胜利者，

你的声誉将如日月永放光芒。

对这一难题来说，首先要面对的是题目中非常复杂的牛群之间的数量关系。事实上，这一问题中涉及四种颜色的牛群中公牛和母牛的个数，因此要求的未知量共有8个。对此，我们可设白色公牛和母牛的个数分别为W、w；设黑色公牛和母牛的个数分别为X、x；棕色公牛和母牛的个数分别为Y、y；花色公牛和母牛的个数分别为Z、z。

先看问题的第一部分，即截止到“但你还称不上聪明无比”之前的部分。这一部分根据已知可列出7个简单的方程，它们将8个未知量联在一起。

第一部分：

对这一部分，可以通过消元解，但因为只有7个方程，因此最终得到的结果是所有8个未知量之间存在的一个比例关系。换句话说，它们都可以表示成同一个变量的整数倍。具体而言，有：

W=10366482a, w=7206360a，

X=7460514a, x=4893246a

Z=7358060a, z=3515820a，

Y=4149387a, y=5439213a

在这无穷多组解中令a=1，可得到满足第一部分的最小正整数解。而由此得到牛群总头数的最小数值为50，389，82。应该说，得到这一答案并不是太困难。正如诗句中所说：“你就不愧为精通算计。但你还称不上聪明无比”。

当考虑第二部分（即从“但你还称不上聪明无比……”之后的部分）时，问题的难度就大多了。这一部分化为数学语言，相当于在前面的基础上又多加了未知量必须满足的两个条件：

W+X为正方形数（8）

Y+Z为三角形数（9）

（9）式中，所谓的三角形数最早由古希腊数学家毕达哥拉斯引入，这类形数意味着，若用小石子个数表示此数字，则可将所有小石子排列成一正三角形，如下图：

由图形知，三角形数一定可以写成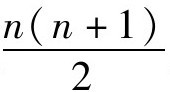，n=1，2，3……

（8）式中的正方形数，即指1、4、9……这样的平方数。

在满足第一部分条件的无穷个整数中找出进一步满足条件（8）与（9）的最小整数解是一个真正的挑战。面对如此棘手的问题，2000年里没有取得真正的进展。

直到1880年，德国数学家昂绍尔对此做出了解答。他先证明了，整个问题可转化为求解不定方程t2-4729494u2=1。具有这种形式的方程正是佩尔方程之特例，虽然当时理论上已经有了求解这一方程的方法——连分数法，然而对这个庞大的方程来说，需要的计算量太大了。结果在经过大量复杂的计算后，昂绍尔确定出，而牛群总数为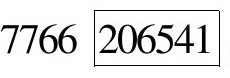，此处表示在前面给出的4位准确数字之后还有206541位数。因此，牛的总数的最小解是一个有206545位的巨数！对这个天文数字的解昂绍尔评价说：“一个大的七位对数表包括每行50个字共50行的一页纸，也就是2500个字；因此对8个未知量中的任何一个想写出它的结果要用张纸，若写出所有的8个未知量要用660页的一卷书”。西西里小岛上决不会容下这样一群牛。“即使它们是最小的微生物——不，即使它们是电子，一个以从地球到银河的距离为半径的圆也只能包含这种动物的很小一部分。”

在昂绍尔的工作之后，从1889年到1893年，伊利诺斯州希尔斯波罗的数学俱乐部算出了头32位数字（其中30位后来被证明是正确的）及最右端的12位数字。1965年，加拿大滑铁卢大学的威廉等三个人用IBM 7040计算机经过7个半小时的强力运算第一次得到了完整解，不幸的是，没有人记得保留打印出来的结果。1981年，劳伦斯国家实验室的尼尔逊公布了所有206545位数字，结果以47页硬拷贝缩印发表在《趣味数学》杂志上。整个计算通过一台克雷Ⅰ型超级计算机完成，实际上，尼尔逊解决这一问题的目的正在于利用它来测验克雷Ⅰ型计算机的性能，结果由于解决问题所用时间太短（只花了约10分钟），通过它不足以测验出计算机的性能。于是，尼尔逊又继续用同一程序找出五个新的解答，最大的数目超过一百万位数。

确实，在已经拥有超快的计算机后，在前人眼中显得复杂无比的这一计算现在已经对数学家不构成挑战了。如果再借助某些数学软件包，那这一问题就更根本不值一提了。事实上，一位西方学者在计算机上用一套名为“Mathematica”的计算机代数软件包在几秒钟内就完成了同一计算。有意思的是，这位学者发现这一软件还能够得出一个计算整个牛群牛的总数的精确公式，而数学家们以前并未想到有这样一个公式存在。在1998年4月的“美国数学月刊”上他发表了一篇论文，详细地介绍了自己的结果：牛的总数为大于的最小整数，其中

p=25194541，q=184119152

a=109931986732829734979866，232821433543901088049

b=50549485234315033074477819 735540408986340

整个计算花了一个半钟头的时间。

一个流传已久的难题有了完整的答案。然而，我们还有疑问要考虑：这个冠以阿基米得之名的难题是否真的由阿基米得最早提出？阿基米得是否解决了这个问题？

对第一个疑问，尚有争论。有人认为“群牛问题”可能在阿基米得之前就早已存在，阿基米得可能只是重新研究而已，至于后来把阿基米得的名字冠于前只是表明其超难。更多人认为这一难题确实源自于阿基米得，至少附有最后两个条件的完整叙述始于阿基米得。即便如此，一般观点也认为莱辛所发现的手稿不太可能出自阿基米得之手。因为阿基米得其他论文都是用命题形式表达的，而这篇却用了讽刺诗的形式。

对第二个疑问，人们普遍认为答案是否定的。人们确信阿基米得曾研究过这个问题，但考虑到解决这个问题需要涉及的困难及巨大的数目，人们有充分理由怀疑阿基米得能解决这个问题。我们已看到，完整的答案是借助计算机的帮助得到的，用手算来解决这个问题所需要的时间长得不可想象。实际上，我们所能确定的只是古希腊人提出了这个最终可归结为一个佩尔方程的著名难题，也因此我们把佩尔方程的源头追溯到古希腊，但关于佩尔方程他们并没有留下任何研究结果。真正对佩尔方程做出探讨并得出重大发现的是古印度人。