柏拉图之于数学

数学，或至少几何学，为在我们周围的流动的物质世界与平静的、理想的、完美的思想世界之间的鸿沟提供了一个直接的例证。从先于柏拉图的时代直到今天，我们拥有完全严格的直线、圆以及类似的定义，但物理世界却不包含没有宽度的完美的直线，也不包含完美的圆，至少我们看不到它们。也许无宽度的直线和完美的圆，以及类似的东西，是我们居于其中的物理空间（或时空）的一部分，但即使如此，我们从未以任何物理的方式遭遇过它们。而如果这样，那在几何学中我们所学习的是什么，我们又是如何学习它的呢？

众所周知，柏拉图相信几何学命题是客观地为真或为假的，独立于数学家的心灵，语言等等。用第2章的术语来说，他是一个真值实在论者。在整个对话中，这种实在论在一定程度上是被预设的，而不是被论证的。恐怕也没有更好的选择。但几何学是关于什么的呢？它的本体论是什么？几何学是如何被知的呢？柏拉图坚持认为几何学的研究对象是独立于人类心灵、语言以及以及诸如此类而存在的对象组成的领域。他从真值实在论来论证本体论实在论，而后者则是随后整个历史发展中不断被回应的主题。柏拉图的引起争议的主要论断牵涉几何学对象的本质和几何学知识的来源。他相信几何学对象不是物理的，而是永恒不变的，至少在这个意义上，几何学对象类似于在的世界中的相。因此他会拒绝上面提到的几何学对象存在于物理空间中的意见。

在《理想国》第6卷的末尾处，柏拉图给出了一个划分线段的隐喻（见图3.1）。变的世界在底部，而在的世界在顶部（善在所有事物之上）。线段的每一部分再进一步划分。变的世界又分为处于顶部的物理对象的领域和底部的对它们的映像（例如，在水中）。而在的世界划分为顶部的相和底部的数学对象^[1]。这暗示物理对象是数学对象的映像，而后者则是相的映像。

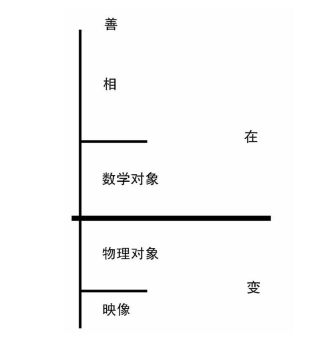
图3.1　划分的线段

然而，有证据显示，包括一些亚里士多德提供的证据，柏拉图至少把某些数学对象视为相。有迹象表明在其新毕达哥拉斯主义的后期，柏拉图认为所有的相都是数学的。有记载说，在一次关于善的公开演讲中，使其听众大为失望的是，柏拉图谈论的几乎都是数学的事情。

我们无需纠缠于解释的细节。所有时期和所有阐释的共同线索是：柏拉图的几何世界是与物理世界相分离的，而更重要的是几何学知识与感觉观察相分离。如上所说，几何学知识得自纯思想或得自对我们过去所熟知的几何学实在的回忆。

涉及本体论，至少就认识论的否定方面来说，柏拉图的论证并不像其表现的那样简单。几何学命题涉及没有广延的点、没有宽度的完美直线和完美的圆。物理世界不包含任何这类事物，我们看不到欧几里得点、线和圆。因此，几何学不是关于物理世界，即变之世界中的任何事情的，我们也不是通过感觉把握几何学对象的。当然，有些物理对象近似于欧几里得图形。一只橙子的周长和仔细地画在纸上的圆或多或少地类似于欧几里得圆，橙子少一些，画出的圆多一些。但几何学定理并不应用于这些近似。例如，考虑圆的切线与圆相交于单独一点这个定理。即使仔细地画圆和切线，用精妙昂贵的工具或削得非常尖的铅笔（或高分辨率的打印机），仍将看到线与圆的边界相重合于一个小的区域，而不是单个的点（见图3.2）。如果用粉笔在黑板上或用棍子在沙子上做以上练习，重合的区域将会大大扩大。当然，这不能否证圆与切线相交于单独一点这一标准定理。柏拉图的解释直截了当，所画的圆和切线只是真实的圆和真实的线的拙劣近似，而后者只为我们的心灵所把握（或回忆）。所画图形相重合的区域只是点的拙劣近似。

图3.2　圆的切线

我们现在可以更好地理解第1章所引述的，柏拉图在《理想国》第7卷中的议论了：

［几何］科学与它的行家使用的语言完全相反……他们的语言再可笑不过……他们似乎在说他们正在做什么事情，又似乎他们所有的语词都是直接指向行动……［他们谈论］关于“化方”、“作图”、“延长”等等。而事实上这门科学的真正目的是纯粹为了……关于永恒事物的，而不是关于某种有时产生和灭亡的事物的……知识。

若柏拉图在几何学涉及的是在的世界中永恒不变的项目这一点上是正确的，那么几何学中就不应有动态的语言。例如，欧几里得《原本》中的构造对柏拉图主义者来说就没什么意义。据15世纪的新柏拉图主义者普罗克洛斯（Proclus）（1970）所言，关于“我们如何能在固定不变的几何学对象中引入运动”的问题占据了柏拉图学院其后几代最优秀的人的心灵。

类似的问题还涉及几何学证明中经常伴随的图形。一个柏拉图主义者会担心它们可能使读者误以为那个定理是关于所画的物理图形的。那么，图形的目的究竟是什么呢？柏拉图也许会解释说，图形会帮助心灵中永恒不变的几何领域，或帮助我们回忆起在的世界。然而，人们可能会对这如何可能而感到疑惑，因为在的世界不是通过感觉达到的。在《理想国》（510d）中，柏拉图写道：

你也知道，虽然他们利用各种可见的图形，讨论它们，虽然他们心中想的实际上是这些图形所摹仿的那些东西。例如，他们所讨论的并不是他们所画的某个特殊的正方形或某条特殊的对角线等等，而是正方形本身、对角线本身等等。他们所画的图形和所做的模型乃是实物，可以拥有其水中的影子或影像。但是现在他们又把这些东西当作影像，而学生实际要把握的则是只有用思想才能理解的那些实在。

这里有与线喻中相同的隐喻：映像和影像。我假设高水平的数学家不需要图形，就能更直接地触及几何世界。柏拉图并非最后一个对图形在几何证明中所扮角色感到困惑的哲学家。

虽然如此，随后的柏拉图主义者没有接受柏拉图的认识论中更神秘的方面，他们中的大多数坚持认为几何学知识是先天的、独立于感觉经验。也许在把握相关概念时某些感觉经验必不可少，或者我们也许以画图作为心灵的视觉助手，抑或为了唤醒心灵对关于欧氏空间的永恒不变的几何领域的记忆。但无论如何，关键之处是数学知识原则上独立于感觉经验。这里主要的根据来自柏拉图的本体论。几何学不是有关物理空间中的物理对象的。

这种观点还有一个待解释的问题是为什么几何学应用于物理世界，即使是近似的。在《蒂迈欧篇》（Timaeus）中，柏拉图讲述了一个详细的，但却是玄思的故事，说的是物理世界是如何从5种所谓的柏拉图体：四面体（棱锥）、八面体、六面体（立方体）、二十面体、十二面体，几何地构建起来的。

柏拉图关于算术和代数的观点，其细节处不像他对几何的说明那样直截了当，但大致的图景是一样的。他在真值和本体论上都是一个直截了当的实在论者，坚持认为算术和代数命题的真假独立于数学家、物理世界，甚至心灵，并且认为算术命题是关于被称为“数”的抽象对象组成的领域。在《智者篇》（Sophist 238a）中，来客说：“一般我们将数列入存在的事物中。”而泰阿泰德（Theaetetus）回答说：“是的，如果有其他事物存在，那数也存在。”

这一对话有几段是将柏拉图式的区分应用到数上。当然，有物质对象的数，我们可称之为“物理数”。这是变之世界中的数。它们有别于“数自身”，后者不是为感觉，而只为纯思想所把握。

例如，在《斐利布篇》（Philebus 56）中，当谈到算术时，柏拉图让苏格拉底在“普通人”和“哲学家”之间作了区分。在某种意义上，有两种不同的算术。对话者，即普罗塔库斯（Protarchus），问道：“这一区分……是基于……什么原则呢？”苏格拉底答道：“的确，普通算术家用不等的单位运算；他的‘二’可能是两支军队、两头牛或任何两个事物，从世界上最小的到最大的，而哲学家则与其无关，除非他同意使其单位的每个例示与这个单位的其他无穷多个例示都完全相等。”还可参见《泰阿泰德篇》（Theaetetus 196，《理想国》525）。这样，我们就看到算术，与几何一样，只是近似地，或只是在对象能够相互区分的意义上，应用于物质世界。哲学家的算术只能精确严格地应用于在的世界。

关于柏拉图对数的本性的看法并无一致的意见。有一种解释认为柏拉图把数看作几何量的比值^[2]。例如，数4就是正方形的周长与其一条边的比值，也是正方形的面积与另一条边长为其一半的正方形面积之比。这种解释的好处不仅适用于自然数，而且适用于（正）有理数和无理数（如在《泰阿泰德篇》这样的对话中所讨论的）。而这种解释的不足则是它不能说明数在几何学语境之外的应用。即使我们专注于在的世界，也要计数非几何的量。例如，我们说，一个给定方程有两个根，存在5个柏拉图体，以及有4个小于10的素数。

以上引自《斐利布篇》中的段落提示了对柏拉图算术的另一种说明。当普通算术家数一双鞋时，每只鞋都是一个单位，但两只鞋形状不同，甚至大小也不完全相同。与此相反，当哲学家计数“二”，她指称的是完全相同的一对单位。对哲学家来说，自然数是相互不可区分的纯单位的集合（《理想国》，425；《智者篇》245）。

顺便要提请注意的是，无论对普通人还是对哲学家，“数”总是此物或彼物的数。普通人的数是像军队和牛这样的集合的数。哲学家的数是纯单位的数。

把称之为“算术”的关于数的理论与称之为“逻辑斯蒂”（logistic）的关于计算的理论区分开来，这是有其古老源泉的。多数作家把后者视为实践的学科，涉及测量和商业贸易（例如，Proclus 1970：20）。人们或许认为这种区分很适合柏拉图，因为他将在之世界和变之世界完全对立。算术会涉及在，而逻辑斯蒂涉及变。然而柏拉图却让算术和逻辑斯蒂都专注于在的世界。不同之处在于自然数本身如何被研究。算术“处理偶数和奇数，关注的是每种数各有多少”（《乔治亚篇》（Gorgias），451）。如果“一个人完全掌握算术的艺术”，那“他也就完全了解了数”（《泰阿泰德篇》，198）。柏拉图的逻辑斯蒂与算术的区别在于它对偶数和奇数的研究，是着眼于它们自身和相互计算的数目这一方面（《乔治亚篇》，451）。这样，算术单个地处理自然数，而逻辑斯蒂则涉及数之间的关系。对逻辑斯蒂，柏拉图提出了自然数如何从其他自然数“产生”（通过日晷的指针）的原则。这类似于以公理化处理本体论的起源。

柏拉图说，为了知，人们应当既从事算术也从事逻辑斯蒂。正是通过研究数本身，以及数之间的关系，灵魂才能把握数的如其所是的本性。正像克莱因（Jacob Klein）（1968：23）指出的，理论化的逻辑斯蒂“成长为一门清晰的关于数之间的关系的科学，……先于，事实上必须先于，所有的计算”。柏拉图的逻辑斯蒂之于实际计算就如同几何学之于画在纸上或沙子上的图形。

也许人们想知道的正是，在克莱因看来（1968：20），柏拉图的算术，与其逻辑斯蒂相对，研究的是什么。大致上，计数的艺术——朗读数字——是算术最拿手的。而“加法还有减法只是计数的扩展”。还有，“计数本身已经预设了被数事物之间的连续关联和区分，同样也对数预设了这些”。克莱因（1968：24）尝试作出结论说，逻辑斯蒂涉及纯单位之间的比值，而算术涉及计数、加法和减法。在后期对话中，也许更适宜把柏拉图的逻辑斯蒂理解为我们所谓的“算术”，即对自然数的数学研究。柏拉图的算术是更高哲学的一部分，在其中人们逐渐把握数本身的形而上学性质。