离散数据的常用预处理方法

2.5.2　离散数据的常用预处理方法

假设下面的n行p列数据矩阵代表n个样本的p个变量测试

数据

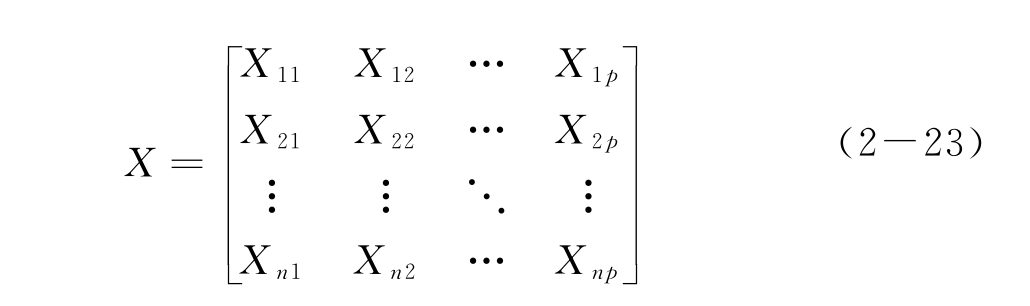
该数据矩阵的质量将直接影响到信息解析和抽提的效果，由于p个变量的量纲和变化幅度可能不同，其绝对值大小可能差很多倍。例如，有的变量为谱图数据，有的变量为化合物的物理化学性质或结构方面的信息，变量间不仅量纲不一样，其绝对值大小也可能会有几个数量级的差别。如果不对原始数据进行预处理，一些数量级较小变量的作用就无法在后面的分析过程中体现，而通过对原始数据的预处理，可以消除量纲和变化幅度不同带来的影响。下面介绍几种常见的数据预处理方法。

1.中心变换（Data　centralization）

中心变换也称均值中心化，就是将原数据矩阵的每一个元素减去该元素所在列的均值

其中x_ij为原始测量值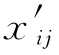，是均值中心化处理后的第i行第j列元素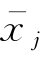，是矩阵X中第j列n个样本的均值。在样本数据集中，当变量类型基本相同、大小范围基本一致时（如X全部由光谱数据组成），常用此法。中心变换后的数据矩阵X′具有每一列均值均为零的特点。

2.对数变换（Natural logarithm transformation）

当x^ij＞0时，对矩阵X中的每一个元素做对数变换（可以是常用对数或自然对数，也可以是以其他整数为底的对数）

当变量的动态范围较大，如相差几个数量级时，常用此法。

3.正规化变换（Normalization transformation）

将原始数据矩阵的各元素减去该元素所在列的最小值后再除以该列元素的极差（极差为该列元素的最大值与最小值之差）称为数据正规化变换

其中min（x_j）和max（x_j）分别为矩阵X中第j列元素的最小值和最大值。这种方法可将量纲不一、范围不同的各种变量或特征数据表达为0～1内的数据。该法不仅适用于同类型、同范围大小的原始数据的预处理，也适用于不同数据类型和范围大小的数据处理。

4.自标度化处理（Autoscaling）

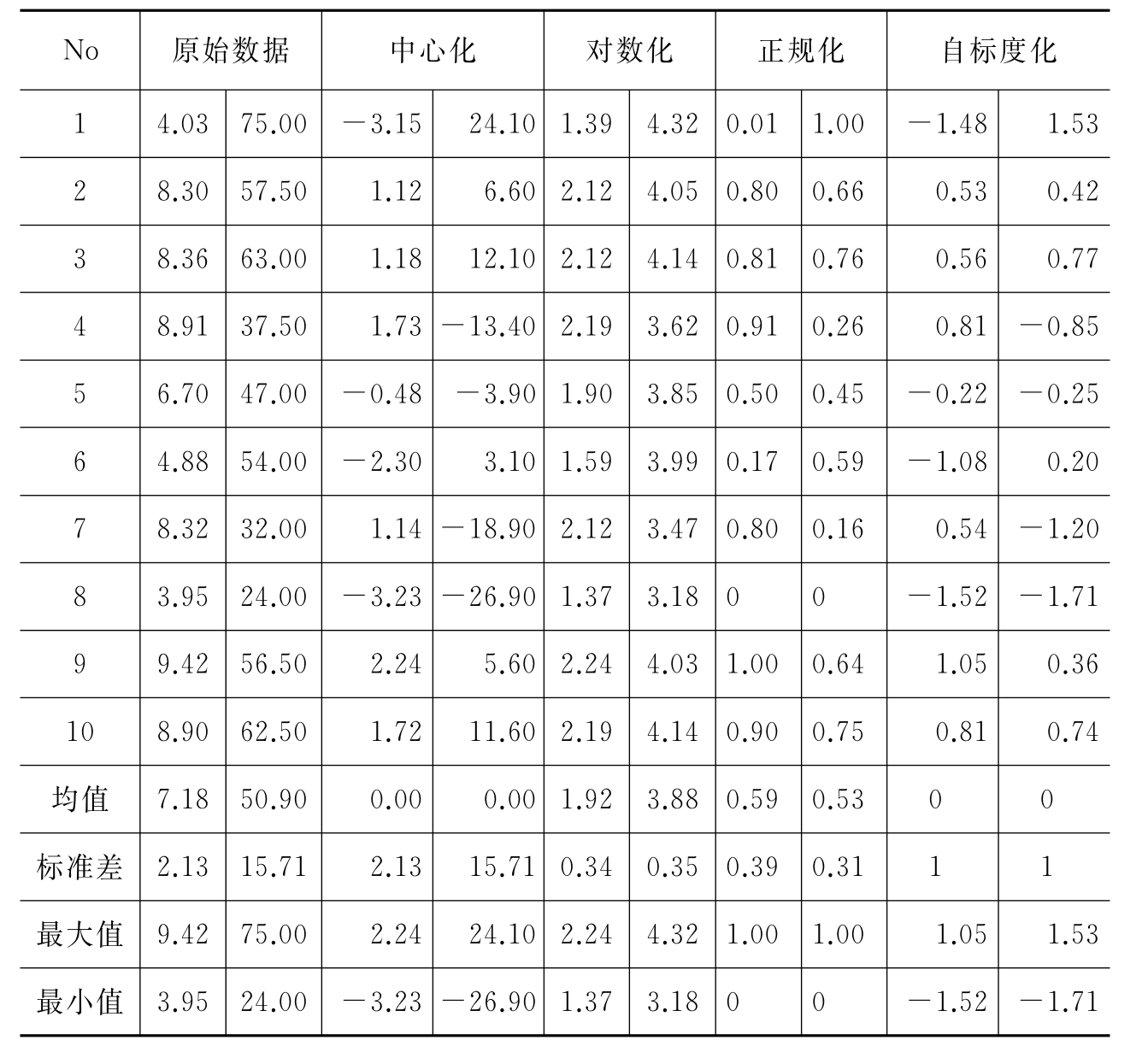
自标度化变换即将各变量化为均值为0，方差为1的变量，也称均值方差化或方差归一化。即将原始数据矩阵中的各列元素减去该列元素的均值后再除以所在列的标准差

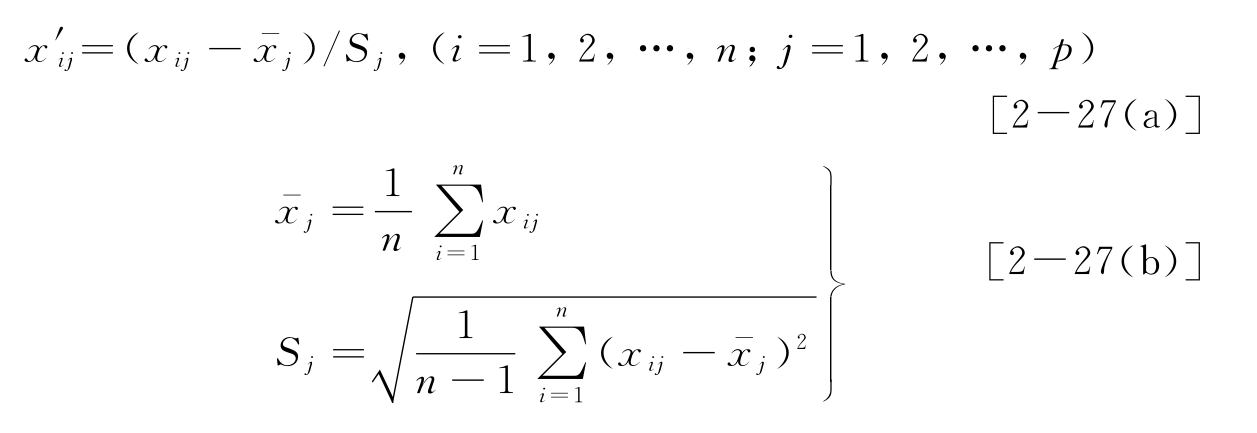
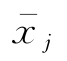与S_j分别为矩阵X的第j列元素的平均值和标准方差。经过标准化处理的变量（一列元素）权重相同，均值都为0，方差或标准差均为1。这是一种运用比正规化处理更广泛的数据预处理技术。

5.标准化处理

标准化预处理的方法很多，对不同的仪器有不同的方法，如在色谱数据中常采用面积归一化的方法，以减小进样误差的影响，即

对于质谱数据则常采用最大归一化预处理的方法，即

值得注意的是，数据经处理后失去了原来的量纲，只是保持其相对大小而已。

例2－18　有10个样本，每个样本由2个变量构成的原始数据矩阵见表2－6的第2列，对这些数据分别进行中心化、对数化、正规化和标准化预处理的结果见第4～11列。

表2－6　10个样本的两个特征变量的原始数据及其预处理结果

在MATLAB下对表2－6中数据进行预处理的命令如下。

（1）数据导入

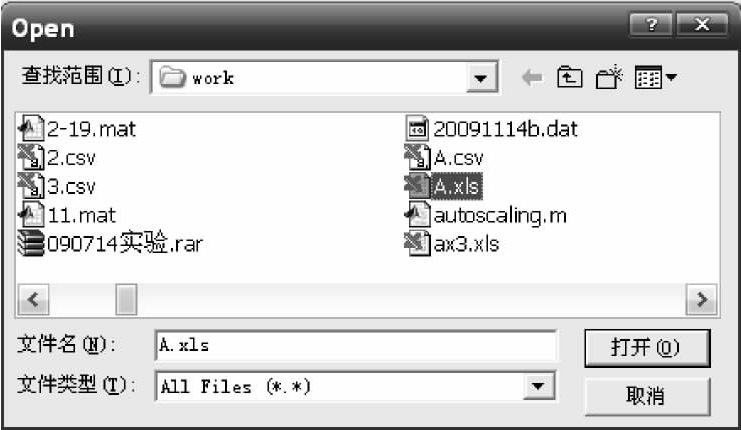
将表2－6中的原始数据用excel存储在MATLAB/work目录下一个名为A.xls文件中，在MATLAB的界面选择“open file”图标双击，在“文件类型”框中选择“All Files（＊.＊）”，然后选择work子目录下的A.xls文件，会出现如下界面

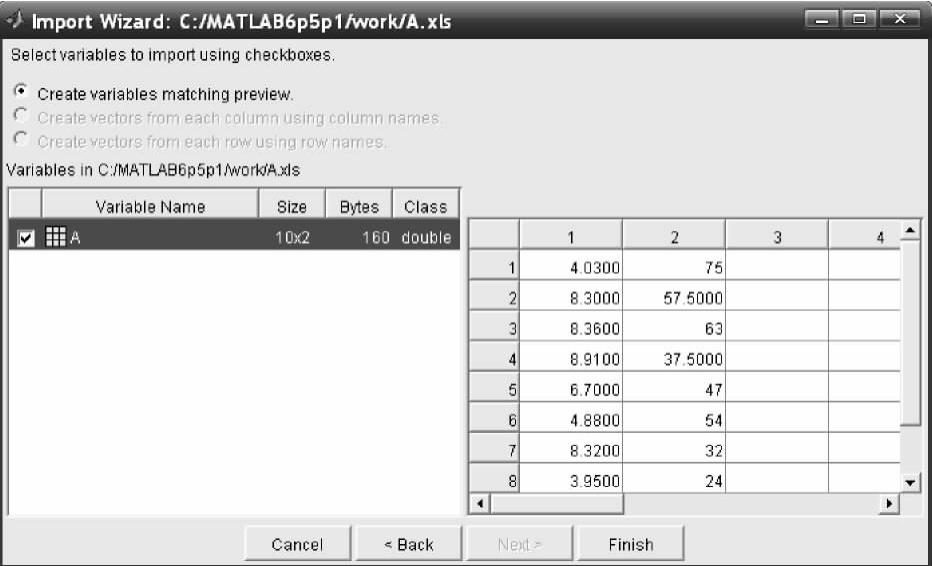
双击该界面“打开”按钮，会出现如下界面

双击上图中的“Finish”按钮，会出现如下文字

Import Wizard created variables in the current workspace.

表示数据文件A.xls已经导入MATLAB的workspace工作目录中（所有MATLAB计算的输入和输出数据均保存在此目录下）。

我们将导入的A变量存为.mat格式的文件，需输入如下命令

＞＞save　A.mat

然后输入clear命令，即清除workspace目录中的变量A，可以看到输入该命令后，workspace中没有任何变量了。

利用load命令来导入已经存入matlab中的变量A，键入如下命令

＞＞load　A

此时可以看到A变量又重新导入workspace目录中了。

（2）求原始变量的均值、标准方差、最大值与最小值

在MATLAB下输入＞＞mA＝mean（A，1）　%mean（A，1）求矩阵A的列均值；mean（A，2）求矩阵A的行均值

可得

mA＝7.1770　　50.9000

即原始变量1和原始变量2的均值分别为7.18和50.90，见表2－6中12行2、3列。

在MATLAB下输入命令＞＞stdA＝std（A）　%求矩阵A的列向量的样本标准方差

可得

stdA＝2.1289　　15.7123

即表2－6中原始变量1和2的标准方差分别为2.13和15.71，见表2－6中13行2、3列。

在MATLAB下输入命令

＞＞maxA＝max（A）%求矩阵A每一列中的最大值

可得

maxA＝9.4200　　75.0000

即表2－6中原始变量1和2的最大值分别为9.42和75.00，见表2－6的14行2、3列。

在MATLAB下输入命令

＞＞minA＝min（A）%求矩阵A每一列中的最小值

可得

minA＝3.9500　　24.0000

即表2－6中原始变量1和2的最小值分别为3.95和24.00，见表2－6中15行2、3列。

（3）进行中心化预处理

在MATLAB下输入命令

＞＞cenA＝A－repmat（mA，10，1）；　%矩阵A的第一列每个元素减去第一列的均值mA（1），第二列减去第二列的均值mA（2）

打开矩阵cenA可得表2－6中2～11行第4～5列所示的结果。

采用（2）中演示的mean、std及max、min函数，可求得表2－6中12～15行第4～5列所示的中心化处理后变量1与2的均值、标准方差、最大值和最小值。

（4）进行对数化预处理

在MATLAB下输入命令

＞＞logA＝log（A）；%对矩阵A的每个元素求以e为底的对数

打开矩阵log　A可得表2－6中2～11行第6～7列所示的结果。

采用（2）中演示的mean、std及max、min函数，可求得表2－6中12～15行第6～7列所示的对数化处理后变量1与2的均值、标准方差、最大值和最小值。

（5）进行正规化预处理

在MATLAB下输入命令

＞＞nmA＝（A－repmat（minA，10，1））./repmat（（maxA－minA），10，1）；

%对矩阵A的每列元素减去列均值并除以该列最大值和最小值之差

打开矩阵nmA可得表2－6中1～11行第8～9列所示的结果。

采用（2）中演示的mean、std及max、min函数，可求得表2－6中12～15行第8～9列所示的正规化处理后变量1与2的均值、标准方差、最大值和最小值。

（6）进行自标度化预处理

在MATLAB下输入命令

＞＞autA＝（A－repmat（mA，10，1））./repmat（stdA，10，1）；

打开矩阵autA可得表2－6中2～11行第10～11列所示的结果。

采用（2）中演示的mean、std及max、min函数，可求得表2－6中12～15行第10～11列所示的自标度化处理后变量1与变量2的均值、标准方差、最大值和最小值。

若将原始数据矩阵及其预处理后每一列数据的分布情况（即每个变量的分布情况）作成示意图2－10，则可看出经过预处理后，数据的分布与原来有本质的不同，不论哪种处理方法得到的数据，其分布范围基本上都统一在同一水平上。

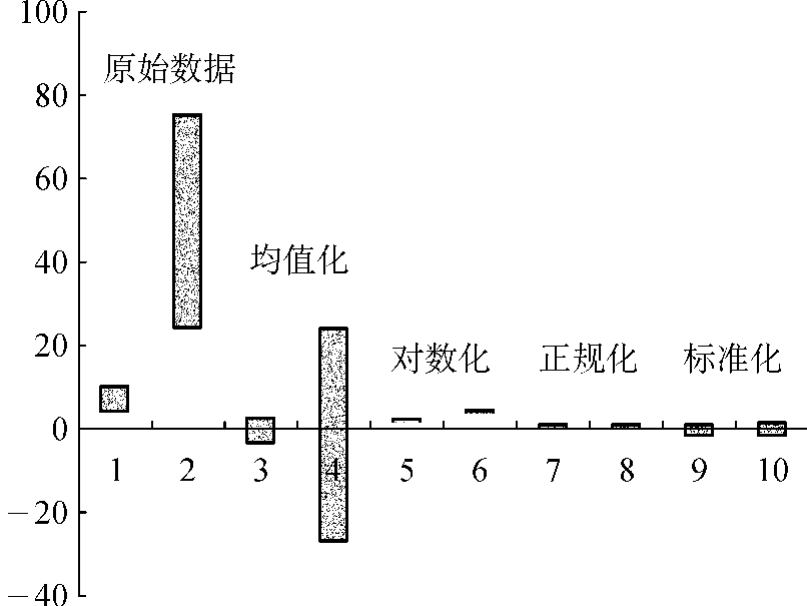
图2－10　原始数据及其预处理后的数据范围分布示意