【摘要】：，βm是m＋1个待定参数，Xij表示第i次实验第j个自变量的值；ε1，ε2，ε3，…式就是多元线性回归数学模型。因而左乘X的转置矩阵XT，使得新矩阵（m＋1）×（m＋1）为方阵，然后再左乘这个方阵的逆矩阵就可求得B。变换过程如下根据式可得线性回归方程的系数。需要注意的是，求逆矩阵时要求两乘积矩阵的维数满足n≥m＋1，即回归模型中方程的个数必须大于或等于参数个数，才能求得各回归系数的唯一解。
4.3.1 多元线性回归方程的建立
如有m个自变量X1，X2，X3，…，Xm，X与Y之间的线性回归方程为
设观察值为（Yi，Xi1，…，Xim），i＝1，2，…，n｛｝，则这n组数据可以表示成如下方程
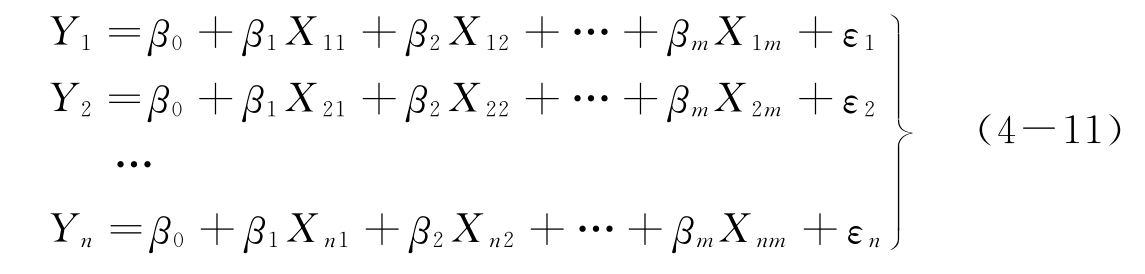
β0，β1，β2，…，βm是m＋1个待定参数，Xij表示第i次实验第j个自变量的值；ε1，ε2，ε3，…，εm是n个独立且服从同一正态分布的随机误差变量。式（4－11）就是多元线性回归（Multi Linear Regression，MLR）数学模型。
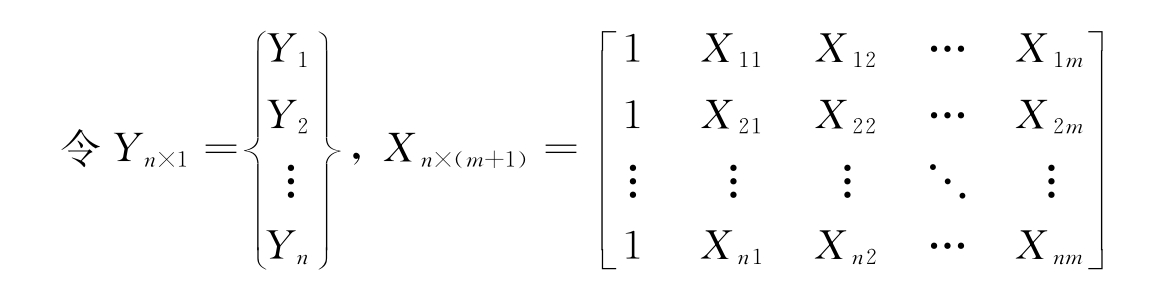
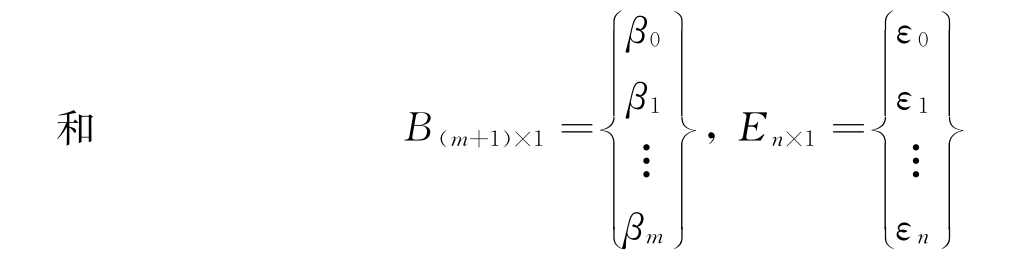
式（4－11）可表达为矩阵形式
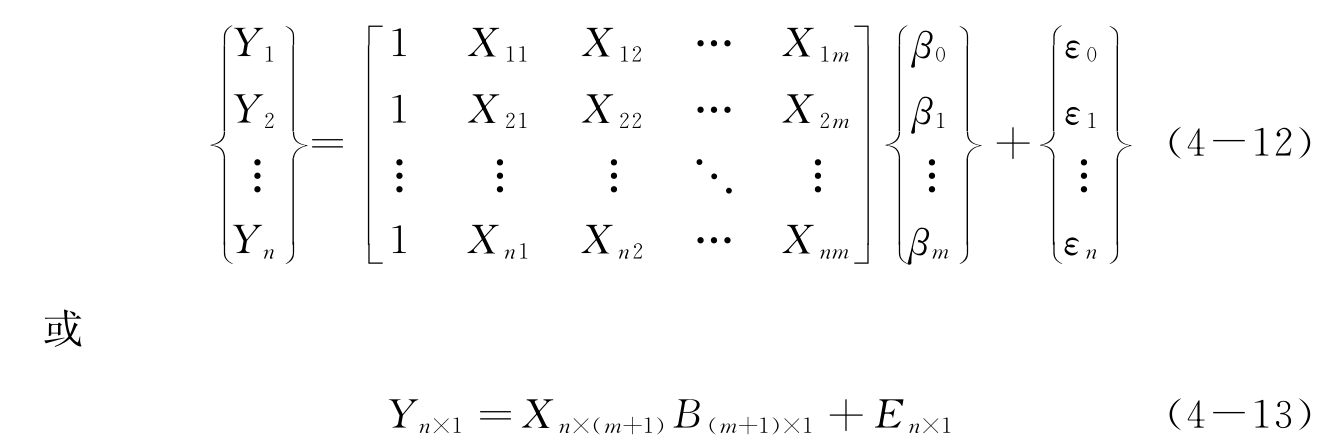
在模型Y＝XB中，要求解系数矩阵B，必须在等式两边左乘矩阵X的逆矩阵。但因Xn×（m＋1）一般不是方阵（m＋1≠n），不能直接求逆，需先将其转化为方阵。因而左乘X的转置矩阵XT，使得新矩阵（XTX）（m＋1）×（m＋1）为方阵，然后再左乘这个方阵的逆矩阵就可求得B。变换过程如下
即待定参数矩阵B可表达为
根据式（4－14）可得线性回归方程（4－13）的系数。需要注意的是，求逆矩阵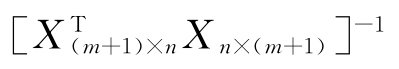
时要求两乘积矩阵的维数满足n≥m＋1，即回归模型（4－13）中方程的个数必须大于或等于参数个数，才能求得各回归系数的唯一解。否则
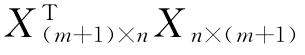为奇异矩阵，无法求逆。
这种数学推导虽不甚严格，但对于方便记忆和快速推导最小二乘解是很有帮助的。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
