特征投影的模式识别方法

8.5.4　特征投影的模式识别方法

对于用p个特征描述的对象，其模式向量含有p个元素，如果p＝2或3，可以在二维或三维空间直观地查看样本在模式空间里的分布情况及相互间的亲疏关系，以便对研究对象进行分类和判别。当p＞3时，则无法直观地根据图形显示来进行判别。

如果p个模式特征可以压缩到二维或者三维空间来表示又不损失太多的信息时，则可以利用第6章介绍的主成分分析、偏最小二乘分解等信息压缩技术将原来的p维空间变量投影到二维或三维空间显示。最常用的就是基于主成分分析的投影判别法。下面以例8－15对该法的基本步骤进行介绍。

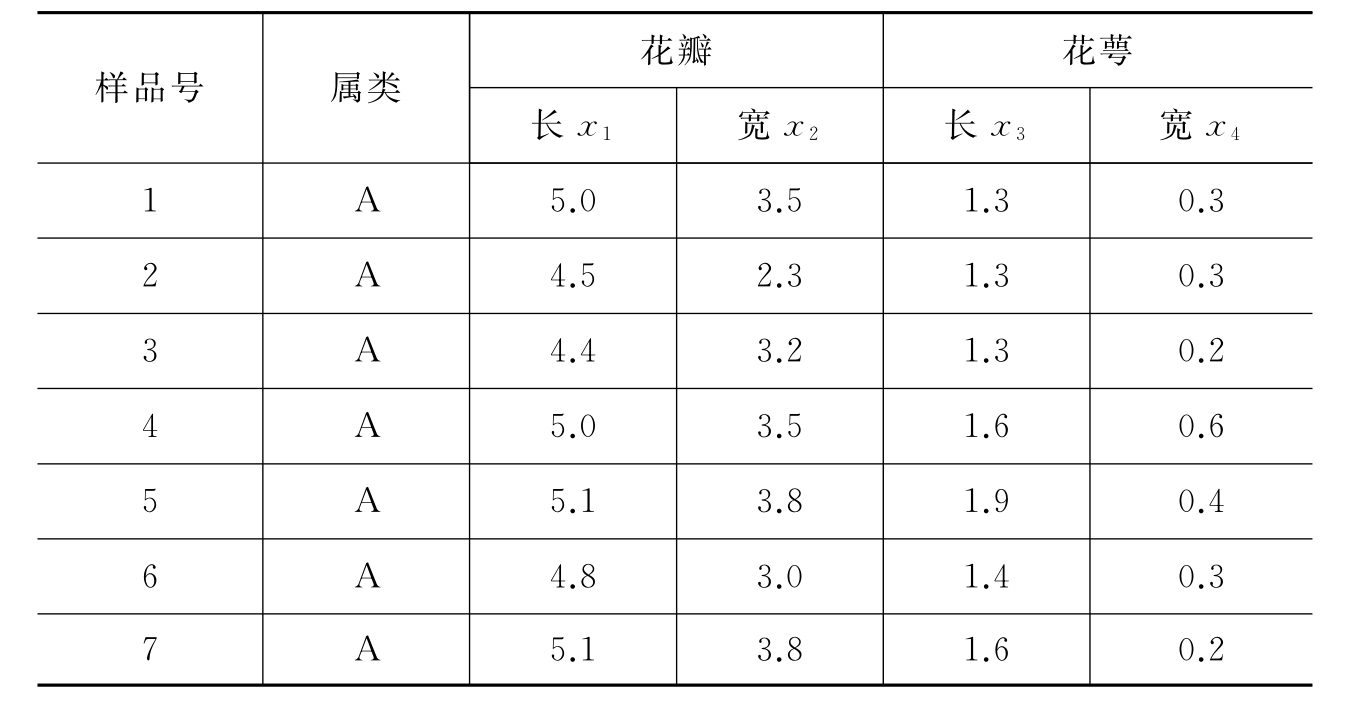
例8－15　表8－8是Fisher在1936年发表的判别两种鸢尾花的测量数据，用四个变量x₁、x₂、x₃和x₄分别表示花瓣长、花瓣宽、花萼长和花萼宽来区分毛鸢尾花（A）和变色鸢尾花（B）。其中21号样本类别未知，待判别。

表8－8　两种鸢尾花的原始测量数据

续表

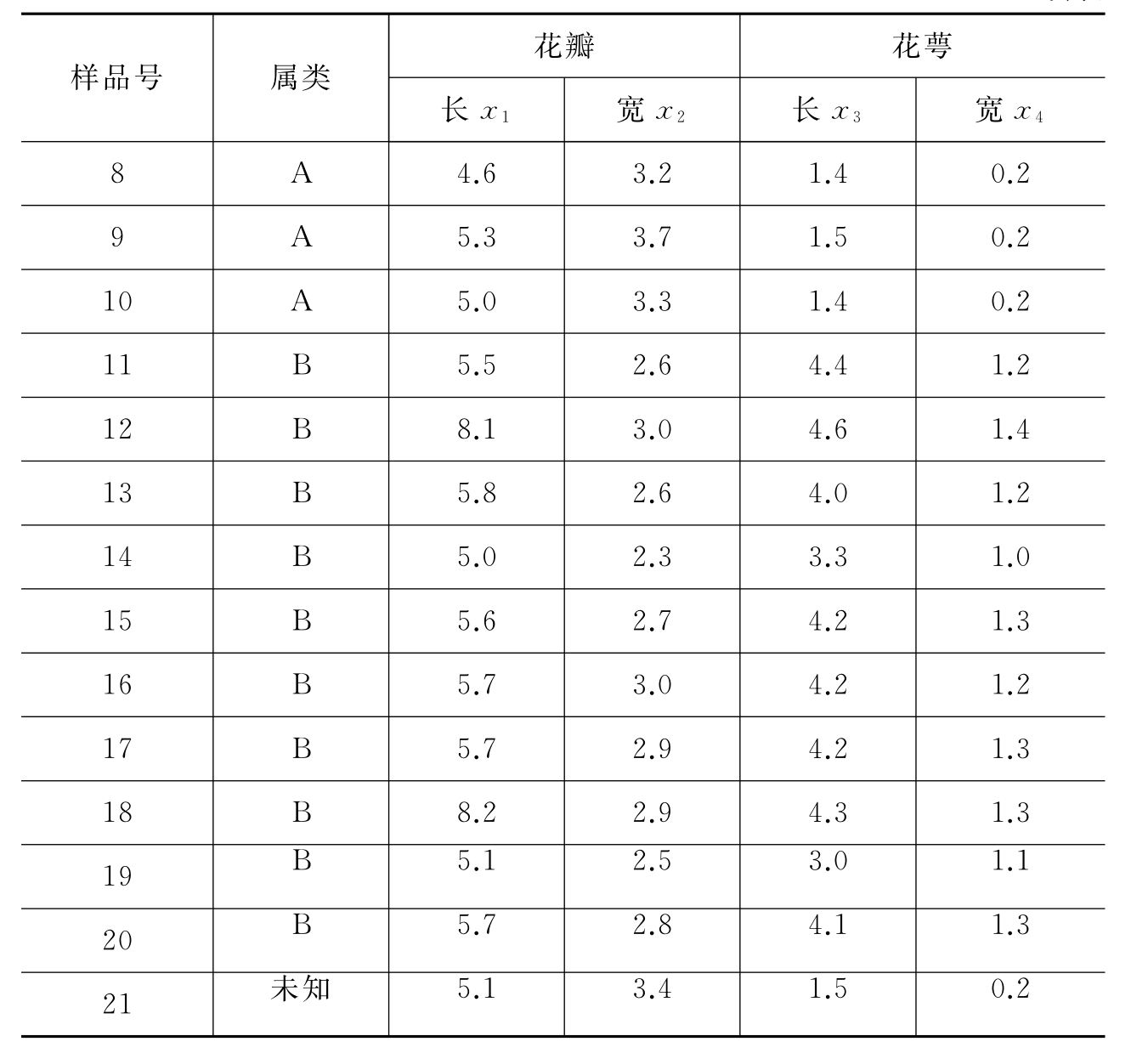
解：（1）对表8－8中的数据进行预处理。

在MATLAB下键入命令

＞＞［ax，mx，sx］＝autoscaling（xx（1：20，：））；%对建模集中20个样本的原始变量进行自标度化预处理，使每个新变量ax的均值为0，方差为1，mx为原始变量的均值，sx为原始变量的方差

（2）对ax中的前20个样本（建模集）进行主成分分解。

在MATLAB下键入命令

＞＞［pc，score，lmd，tq］＝princomp（ax（1：20，：））；%对建模集中预处理后20个样本的变量进行主成分分析

打开pc矩阵，其第1，2列即为第1、2载荷轴

打开lmd可得主成分方差

在MATLAB下键入命令

＞＞varpercent＝cumsum（lmd/sum（lmd））

%计算各主成分的累积贡献率并返回给向量varpercent。

可得

由此可见前两个主成分的方差占总方差的93.83%，可以反映原来四个变量的绝大部分信息。

（3）求未知样本的前两个主成分得分。

在MATLAB下键入命令

＞＞　axu＝（xx（21，：）－repmat（mx，1，1））./repmat（sx，1，1）

%将未知样本的变量减去建模集样本对应变量的均值并除以方差

可得

在MATLAB下键入命令

＞＞scu＝axu＊pc（：，1：2）　%求第21个（未知）样本的前2个主成分得分

可得

即样本21的第一、二主成分分别为－1.6326与－0.3784。

（4）将21个样本投影在第一、二主成分轴上。

在MATLAB下键入命令

可得如下投影图

图8－11　21个鸢尾花主成分投影

由图8－11可看出，两类鸢尾花样本在第一、二主成分投影图中明显分成左、右两个区间，左边为毛鸢尾花样本，右边为变色鸢尾花样本，未知样本落在毛鸢尾花样本区，应该是毛鸢尾花。

总结本例，利用主成分投影进行模式识别的主要步骤如下。

（1）对原始数据的特征（变量）进行自标度化预处理。

选择自标度化预处理而不选择其他预处理方法是因为主成分分解的原理是基于方差最大化原则进行，将原始特征变量处理成均值为0、方差为1的变量可以消除原始变量因方差量级和大小不同所造成的差异，使每个变量在进行主成分分析之前都具有相同的权重和作用。

（2）对预处理后的数据矩阵进行主成分分析。

（3）求每个主成分的累计贡献率，根据累计贡献率判断前两个（或三个）主成分所包含的信息量。

（4）当前两个（三个）主成分的累计贡献率足够高（如大于90%或85%）时，计算已知样本和未知样本的第一、第二主成分得分并将其在第一、第二主成分轴投影。根据投影图各样本的分布情况判断该投影图可否良好区分已知样本并判别未知样本的归属。

另外还有基于主成分分析的SIMCA方法和基于偏最小二乘的投影判别方法，感兴趣的读者可以参阅相关文献和书籍，本章不再赘述。