−分解及其应用

第四章　互为Hilbert变换对的正交小波构造及其应用

DWT由于缺乏平移不变性等缺陷而阻碍着它的进一步应用。采用a trous算法（或多孔算法）进行非下采样的小波变换可以解决不具有平移不变性的缺点，然而这样做会导致计算量的急剧增加，且使得输出信息存在很大的冗余，给后续处理带来冗余计算。常规复小波在给变换带来一定的冗余的同时也可以克服这个问题，但是超过一层分解的复小波变换的输入是复数形式，要构造它的完全重构的逆滤波器非常困难。

为了解决这些问题，Kingsbury提出了DT−CWT，它既满足完全重构条件，又保留了复小波的其他优点。总的来说，它具有以下性质[104]：具有近似平移不变性；对多维信号具有良好的方向选择性；完全重构特性；有限的冗余度，其冗余性与分解的尺度无关，对m维的信号存在2m倍的冗余；较小的计算量，对m维信号其计算量是原DWT的2m倍。

近年来很多研究者提出，可以同时采用两个互为Hilbert变换的小波对处理信号，通过两个不同系统的综合信息来更有效地表示信号中各向异性的奇异性[96,99,105]。DT−CWT中实际上就用到了两个互为Hilbert变换的小波对[106]。

Selesnick[107]给出了正交小波系构成Hilbert变换对的必要条件，并在文献[90,106]中提出了一种基于延迟滤波器的构造算法。Ozkaramanli等[91]进一步指出Selesnick在文献[107]中给出的必要条件还是充分的。与此同时，Kingsbury[99]从平移不变性的角度提出了一种DT−CWT结构，并给出了相应的构造算法。王红霞等[108,109]也于近期提出了新的互为Hilbert变换对的小波构造方法，取得一定成果。

本章在Selesnick和Kingsbury等人的基础上，结合构成正交小波的充要条件，提出了构造互为Hilbert变换对的正交小波的代数构造方法，并指出构造互为Hilbert变换对的双正交小波也可以用类似的方法。与文献[90]相比，这种小波构造方法更加灵活，适当调整设计参数，可以得到更加对称、更加平滑的小波。

第一节　基于延迟滤波器的构造方法

一维DT−CWT通过一对滤波器组同时作用在输入数据上来实现其对信号的处理。它包含两个平行的小波树，两棵树中的实数滤波器h0(n)和h1(n)、g0(n)和g1(n)各代表了一个共轭正交滤波器对。设这两个滤波器对所对应的实数值尺度函数和小波函数分别为：ϕh(t)、ψh(t)、ϕg(t)、ψg(t)，复小波变换的优点源于复小波函数ψ(t)的频谱单边性，为了具有这种性质，小波函数ψg(t)必须是ψh(t)的Hilbert变换。设H0(w)与G0(w)分别是低通滤波器h0(n)和g0(n)的Fourier变换。

文献[106]指出：如果H0(w)和G0(w)是两个共轭正交的低通滤波器组，并且满足如下关系式：

那么它们所对应的小波互为Hilbert变换对，即：

ψg(t)=H{ψh(t)}

或

则相应的小波滤波器g0(n)与h0(n)相差半个采样的延迟。

为了构造这样的两个正交的小波对，设它们的低通尺度滤波器有如下形式：

h0(n)=f(n)*d(n)

g0(n)=f(n)*d(L−n)

其中滤波器d(n)是能够获得（或近似获得）半个采样延迟的分数延迟滤波器，L为d(n)滤波器的延迟度，f(n)是待求滤波器，*表示求卷积。上式在z域中可表示成下式：

由此得到下式：

则传递函数为：

如果把此传递函数A(z)设计成一个具有半个采样延迟的全通滤波器，即：

A(ω)≈e−jω/2　　　ω在0附近取值

或

A(z)≈z−1/2　　　z在1附近取值

那么式（4.1.4）就可以写成式：

由此近似得到了式（4.1.1）。

下面的问题就是如何设计这个A(z)。

文献[110]提出了一种有τ个采样延迟的Thiran延迟滤波器D(z)：

其中

而

(x)n=(x)(x+1)…(x+n−1)，x=τ−L或x=τ−1

对于D(z)，式（4.1.5）可以改写成式：

A(z)≈z−τ　　　z在1附近取值

或

该分数延迟滤波器d(n)的系数按式（4.1.7）计算：

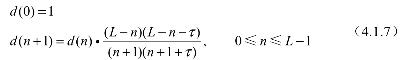
其中：L为分数延迟度（决定着d(n)滤波器长度），τ为采样延迟数，当取τ=1/2时，由式（4.1.4）、式（4.1.5）和式（4.1.6）就得到了式（4.1.1）。

在此基础上文献[90]提出了基于延迟滤波器和谱分解的互为Hilbert变换对的小波构造方法。

第二节　互为Hilbert变换对的正交小波的代数构造方法

根据Selesnick提出的小波互为Hilbert变换对的思想，本章结合构成正交小波的充要条件，提出构造互为Hilbert变换对的正交小波的代数构造方法。

定理 4.1[111]：设φ∈L2(R)是一可积的尺度函数，那么

h[n]=<2−1/2φ(t/2), φ(t−n)>的傅里叶级数满足

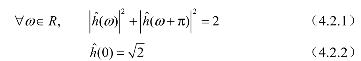
反之，如果以2π为周期，在ω=0的某邻域内连续可微，满足式（4.2.1）、（4.2.2），且

那么

是某个尺度函数φ∈L2(R)的傅里叶变换，其中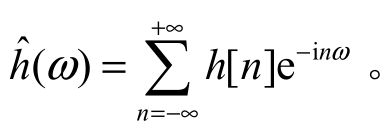

定理4.1说明：任何尺度函数都被一个叫“共轭镜像滤波器”的离散滤波器所确定。传递函数满足式（4.2.1）的离散滤波器叫共轭镜像滤波器。

若φ为正交尺度函数，h={h0,h1,…,hN}是对应φ的双尺度方程的滤波器，则构造正交小波时h应满足以下方程（4.2.3）、（4.2.4）：

其中，当n=0时，δ=1，当n≠0时，δ=0。

定理 4.2[111]：设ϕ和φ是生成一组正交基的小波和尺度函数。设ϕ(t)= o((1+t2)−p/2−1)且φ(t)=o((1+t2)−p/2−1)，则：

（1）小波ϕ有p阶消失矩；

（2）和它的前p1−阶导数在ω=0处为零；

（3）和它的前p1−阶导数在ω=π处为零；

（4）对任意0≤k<p，是一个k阶的多项式。

由定理4.2可以得到[112]：

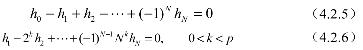
联立式（4.2.3）、（4.2.4）、（4.2.5）、（4.2.6），得到构造有限正交小波滤波器的代数方法。通过解以上方程组得到滤波器h={h0,h1,…,hN}，然后，按下式（4.2.7）：

求出在ω=0～2π范围内的上界值，如果它小于等于2p−1，则h即为所求滤波器[112]。

联立式（4.2.3）、（4.2.4）、（4.2.5）、（4.2.6）、（4.2.7）即得到构造正交小波的充要条件，再结合式（4.1.2）、（4.1.3），可以构造各种互为Hilbert变换对的正交小波。本章提出的互为Hilbert变换对的正交小波的代数构造方法具体步骤如下：

（1）设定消失矩阶数p，滤波器延迟度L；

（2）求解分数延迟滤波器（式（4.1.7）），得D(z)；

（3） 设F(z)为{x1,x2,…,xN}，其中N=2p+2。并分别求出F(z)D(z)、F(z)Z−LD(1/z)的表达式h(n)、g(n)；

（4）求解方程组（4.2.3）、（4.2.4）、（4.2.5）、（4.2.6）、（4.2.7）式，得F(z)；

（5）F(z)D(z)、F(z)Z−LD(1/z)即为所求。

当延迟滤波器长度为3时，其中步骤（3）、（4）中会产生方程个数总是比未知变量个数多4的问题，由于表达式h(n)、g(n)的对称性，由g(n)得到的方程（4.2.3）、（4.2.4）、（4.2.5）这四个方程（式（4.2.3）代表2个方程）总是与h(n)的相应方程完全相同，因而步骤（4）总是可以得到确定解。

用类似的方法可以很方便地构造互为Hilbert变换对的双正交小波。

第三节　构造实例

一、本方法构造的新小波

根据上节提到的步骤，表4.1、表4.2是本章方法构造的两个正交尺度滤波器h、g及其对应的互为Hilbert变换对的正交小波如图4.1、图4.2（部分示例）。

表4.1　本方法构造的互为Hilbert变换对的正交尺度滤波器系数（滤波器长度是12）

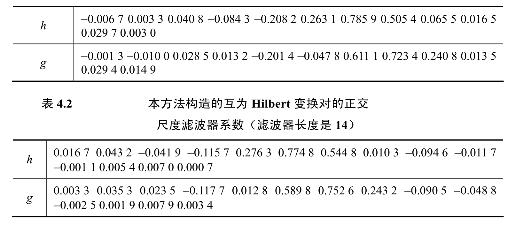
二、降低消失矩得到的新小波

通过降低消失矩同时保持滤波器长度不变，按照前面所讨论的方法还得到了如图4.3、图4.4所示的小波（部分示例），其对应的正交尺度滤波器如表4.3、表4.4。它们均为4阶消失矩小波，滤波器长度均是14。

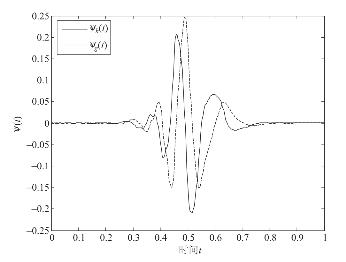
图4.1　表4.1所对应的互为Hilbert变换对的正交小波（4阶消失矩）

图4.2　表4.2所对应的互为Hilbert变换对的正交小波（5阶消失矩）

表4.3　本方法构造的互为Hilbert变换对的正交尺度滤波器系数

图4.3　表4.3所对应的互为Hilbert变换对的正交小波

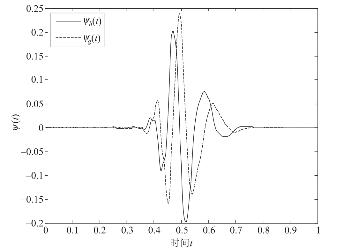
图4.4　表4.4所对应的互为Hilbert变换对的正交小波

表4.4　本方法构造的互为Hilbert变换对的正交尺度滤波器系数

三、本方法构造的消失矩不一样的小波

本方法还可得到消失矩不一样的小波，如图4.5、图4.6所示（部分示例），其中图4.5所对应的正交尺度滤波器如表4.5，h对应的小波是5阶消失矩，g对应的小波是4阶消失矩。

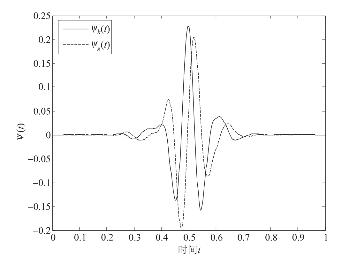
图4.5　表4.5所对应的互为Hilbert变换对的正交小波

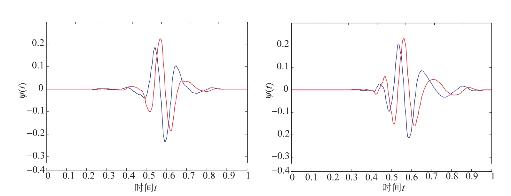
图4.6　消失矩不一样的互为Hilbert变换对的正交小波

注：h对应的小波是5阶消失矩，g对应的小波是4阶消失矩

表4.5　本方法构造的互为Hilbert变换对的正交尺度滤波器系数

图4.6是本章方法构造的另外一些消失矩不一样的互为Hilbert变换对的小波（没有给出滤波器系数）。

第四节　DT−CWT的平移不变性

DT−CWT是一种具有近似的平移不变性、较高的计算效率和可以精确重构等优良特性的离散小波变换形式[113,114]。一维DT−CWT通过一对滤波器组同时作用在输入数据上，它相当于对一个信号同时作两个离散小波变换，这两个小波变换的小波滤波器是特殊设计的，它们互相形成Hilbert变换对。

DT−CWT分解重构过程示意如图4.7[99,115]：

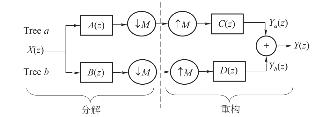
图4.7　DT−CWT的简化的分解和重构的过程示意图

图4.7显示了DT−CWT的简化的分解和重构的过程，所有向上采样和向下采样操作都被移到分解滤波器的输出端和相应的重构滤波器的输入端，M是整个的down/up-sampling factor[115]。重构时对两棵树的结果进行了综合，如下式所示：

通过对滤波器A(z)、B(z)、C(z)、D(z)的特殊设计，使得最后的结果Y(z)获得良好的平移不变性。

具体来说，在正交双通道滤波器组中，分解端低通滤波器设为H0(z)，高通滤波器为H1(z)，相应的合成端滤波器分别为H0(z−1)、H1(z−1)。对于一个输入信号S(z)，通过分解端和向上抽样产生如下的低通系数[103]：

相应的，分解产生的低频部分为：

对于DWT，如果一个输入信号有一个点的时间平移，记作z−1S(z)，通过小波滤波器得到：

其中，代表高频部分，而低频部分为：

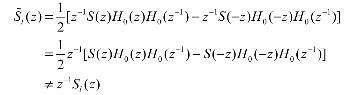
从这个计算中可以看到，DWT是平移敏感的。

对于DT−CWT，应用了一个额外的经过了平移的分解滤波器z−1H0(z)和z−1H1(z)，这两个滤波器组的低、高通道最后被平均。例如，如果两个滤波器组被分别标示为a、b，那么其低通部分可如下表示：

由此可见，在中没有包含混淆项S(−z)，分解结果获得平移不变的特性。

DT−CWT的平移不变性图示效果如图4.8[99,116]所示。可见DT−CWT对消除伪Gibbs现象的能力相对DWT有明显的提高。刘芳、刘文学、焦李成[117]用试验说明了DT−CWT比常规离散小波变换可以取得更好的降噪效果。

图4.8　DT−CWT的平移不变性

S—原始信号，a4—第4层近似系数、d1～d4—第1～4层细节系数的重构信号

第五节　DT−CWT分解及其应用

传统的Fourier变换可有效地分析平稳信号，而对于众多的非平稳故障信号采用小波变换能起到好的分析效果。由于DT−CWT比DWT有更多优良特性，所以本章在此研究了基于本章构造的小波的DT−CWT的一些应用，并与DWT进行了比较。

一、仿真试验

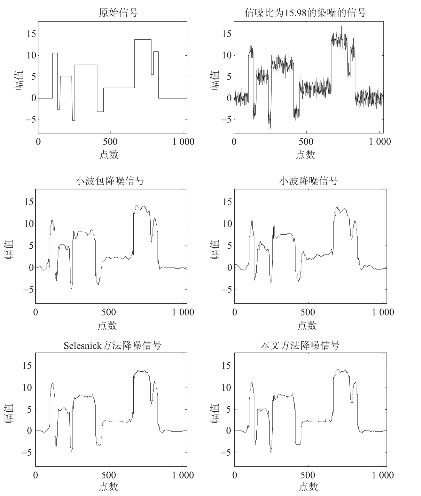
图4.9　Heavisine信号及其降噪信号

对三个典型的非平稳信号Heavisine信号和Doppler信号（它们的原始信号见图1.5、图1.6）以及Blocks信号（如图4.9所示）分别进行降噪处理，其中本文方法是指用本章构造的互为Hilbert变换对的小波（表4.1中的数据）经DT−CWT分解得到的，Selesnick方法是指用文献[90]构造的互为Hilbert变换对的小波经DT−CWT分解得到的。各种方法降噪后的信噪比见表4.6。比较可见：DT−CWT可以得到比DWT更好的降噪效果，而用基于本章构造的小波对的DT−CWT比用Selesnick的方法可以得到更高的信噪比。

表4.6　各种方法降噪后的信噪比 单位：dB

二、应用试验

试验一：轧机齿轮箱的故障诊断

在某钢厂现场的一精轧机齿轮箱上测得有故障的振动加速度信号如图4.10，采样频率是5 000Hz，采样长度是1 024点。

图4.10　原始故障信号

图4.11是用DB4小波经DWT分解得到的各层近似信号（a1～a4）和细节信号（d1～d4）。图4.12是用本章构造的互为Hilbert变换对的小波（表4.1中的数据）经DT−CWT分解得到的各层近似信号（a1～a4）和细节信号（d1～d4）。

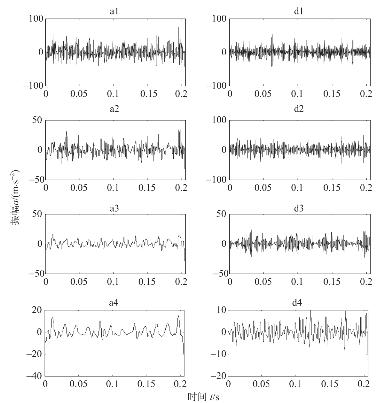
图4.11　用DB4小波经DWT分解得到的各层近似信号（a1～a4）和细节信号（d1～d4）

从图4.12中的a1～a4可以看出：在1 024/5 000=0.204 8（秒）的时间内，非常清楚地出现了12个冲击，这些冲击所对应的频率为12/0.204 8=58.593 75（Hz）。而该精轧机锥箱I轴的轴频的理论计算值是58.594Hz，二者完全吻合。经检查结果是该轧机锥箱轴的轴承偏心，使回转轴每转一周便产生一次振动冲击。而在图4.11中对应的a1～a4低频信号没有图4.12明显。经验证得知：当用DB系列小波经DWT分解得到的相应结果都与图4.11类似，均没有图4.12明显。

图4.12　用本章构造的互为Hilbert变换对的小波经DT−CWT分解得到的各层近似信号（a1～a4）和细节信号（d1～d4）

试验二：转子冲击特征信号的试验分析

试验在Bently RK−4转子试验台（见图4.13）上进行。转子的转频为20Hz，采样频率为8 000Hz，采样点数为1 024点。在转子试验台上附加冲击信号，使转子每转一周就会受到两次冲击。

图4.14为转子受冲击的位移（电压）信号。从图4.14（a）表示的时域图中可以看到转频20Hz的谐波成分，且信号中具有冲击成分，但很难直接从时域图中计算冲击信号的周期。在图 4.14（b）中的信号频域图中出现了 20Hz与40Hz的频率成分。由于转子的转频为20Hz，所以在频域图中一定会出现20Hz的频率成分。但是，如果信号中具有20Hz或40Hz的冲击成分，在信号的频域图中，都会出现40Hz的频率。这样，依据图4.14（b）中出现的40Hz频率成分并不能确认信号中的冲击成分。因此，从原始信号的时域图或频域图中都不能直接判断是否有附加的冲击信号。

图4.13　转子试验台实物图

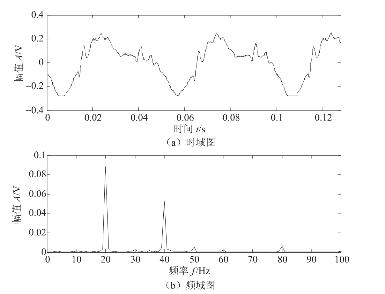
图4.14　转子受冲击的信号的时域图和频域图
（频域图中样本长度采用8 192点）

图4.15是用DB4小波经DWT分解得到的各层近似信号（a1～a5）和细节信号（d1～d5）。

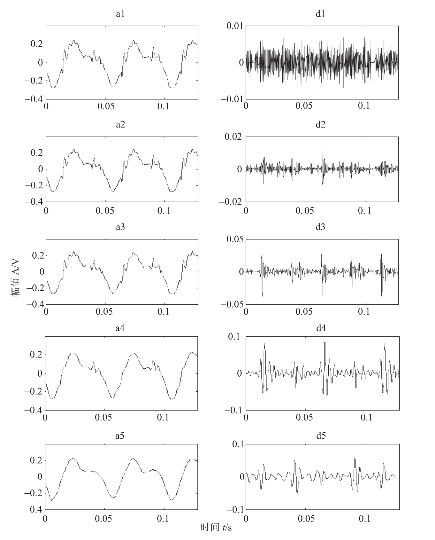
图4.15　用DB4小波经DWT分解得到的各层近似信号（a1～a5）和细节信号（d1～d5）

图4.16是用本章构造的互为Hilbert变换对的小波（表4.1中的数据）经DT−CWT分解得到的各层近似信号（a1～a5）和细节信号（d1～d5）。

图4.16　用本章构造的互为Hilbert变换对的小波经DT−CWT分解得到的各层近似信号（a1～a5）和细节信号（d1～d5）

从图4.16中的d3～d5可以看出：在1 024/8 000=0.128 0（秒）的时间内，非常清楚地出现5个冲击，每两个冲击所对应的时间间隔约为25ms。而在转子试验台上附加的冲击信号的频率是40Hz，即每两次冲击的时间间隔为25ms，二者基本吻合。而在图4.15中对应的d3～d5没有图4.16明显。