阈值降噪法

第六章　基于DT−CWT的块阈值降噪及其应用

上一章所提出的匹配追踪特征信号提取方法，对于提取隐含的冲击信号非常有效，它本质上是一种信号分解方式，与降噪原理相同，但对于降噪而言它通常得不到光滑的结果。而在故障诊断中经常需要降噪，以排除背景信号和噪声的干扰。Donoho提出的小波软、硬阈值降噪法可以满足光滑性的要求，在实际应用中也获得了广泛的应用，接着Cai等提出了块阈值降噪法，这种方法能得到更多的优良特性。本章在第二章构造的小波的基础上，针对第三章所提方法在应用上的某些不足，从另一角度提出了基于DT−CWT的重叠块阈值降噪方法，理论和试验均说明了本方法的有效性。

小波变换被认为是信号的稀疏表示，信号的能量总是集中在小波域中的少数系数上，尤其是集中于信号有突变的地方。而对于旋转机械设备振动信号，无论设备出现什么故障，总会在测量信号中产生异常突变，从而在信号中出现或强或弱的周期性冲击。但是在实际监测中，这种周期性的冲击常常淹没在强的背景噪声中，噪声是影响机械设备早期故障诊断的主要因素，必须通过降噪，去除被分析信号中的噪声和背景信号，凸现故障的特征信息。Jing Lin和Liangsheng Qu［140］提出了一种基于morlet小波基的CWT降噪方法，并指出用该方法可以从含有大量噪声的齿轮箱振动信号中完整地提取出周期性冲击信号。吕志民、徐科和徐金梧等［26，27，141，142］提出用奇异谱降噪法、局部投影法、小波、基于相重构和主流形识别的非线性时间序列降噪方法提取弱特征信号，取得了满意的效果。

目前基于小波阈值的降噪方法有多种，如：统一阈值、极小极大阈值、无偏风险估计阈值、交叉验证阈值等，已经在信号处理、图像处理等领域得到了广泛的应用。这些方法都是采用逐项阈值（term by term thresholding），考虑了每一个系数的整体统计特性，然后估计阈值大小。这种阈值去噪算法对每一个小波系数进行独立的估计，并与设定的阈值比较，周围的小波系数对其没有影响。这种方法获得了方差与偏差的折衷，但这个折衷不是优化的，抛弃了太多的系数，造成估计子偏差过大。

Cai等［143］提出了NeighBlock块阈值去噪的方法（DWT_NeighBlock），分块对小波系数进行阈值操作，能充分利用邻域小波系数的信息，提高了估计的精度以及收敛的速度。但是DWT_NeighBlock采用的是常规的离散正交小波变换（DWT），而基于DWT的降噪会产生伪Gibbs现象，使降噪后的信号在急剧变化部分产生振荡现象，从而对具有奇异点或不连续点的信号的降噪效果影响比较大，这对于在强噪声背景下提取出弱信号影响尤其明显。

本章由此提出一种基于DT−CWT的NeighBlock的降噪方法（DT−CWT_ NeighBlock），并将其成功应用于机械故障诊断中。理论和试验均可以说明，这种方法能获得比DWT_NeighBlock降噪法更好的效果，不仅能有效抑制高斯白噪声，还能够去除脉冲噪声，可以更好地凸现故障信息，因而可以为机械设备的故障诊断提供一种新的方法。

第一节　VisuShrink阈值降噪法

块阈值法是在VisuShrink等经典的逐项阈值法的基础上发展而来的，因此了解一下该方法是有必要的。

假定观察信号s是等间隔采样且其模型如下［93］：

s=f+σz

其中，f是未知的纯净的信号；z为独立同分布的高斯噪声，其均值为零，方差为1；未知参数σ为噪声的强度。

降噪的目的是从含噪的信号s中估计出真实的未知信号f，估计性能由估计信号与真实信号f的均方误差即风险衡量，定义为：

该观察模型在小波域中可表示为：

ν=Ws=Wf+σWz=w+σz*

其中ν是长度为N的观察信号s的小波系数；W为对应于离散小波变换的N×N正交矩阵；w为真实信号的小波系数；z*为噪声z的小波系数。

正交小波变换有一个基本的统计特性：时间域的白噪声z经变换后在小波域仍为白噪声z*，且正交小波变换保持l2范数不变，因此上述风险式（6.1.1）可表示为：

这就把问题转化为估计小波系数及相应的风险。

Donoho和Johnstone由此提出了基于VisuShrink阈值的小波收缩的去噪方法［144，145］。它在不需要任何先验知识的前提下，从含噪的观察信号中估计出真实信号，并从渐进意义上证明了小波收缩的最优性，任何其他的线性估计都达不到相同的估计效果。其去噪方法是充分利用了正交小波基的特点及信号与噪声正交小波变换的不同特性：小波变换的稀疏性及去相关性保证了真实信号小波变换的能量集中在有限小波系数上，而白噪声变换后仍为白噪声，能量均匀分布在所有小波系数上。根据这些特性，小波消噪主要分为如下步骤：

第一，对观测信号进行正交小波变换，由时间域转化到小波域，得到观察信号的小波系数；

第二，估计噪声和选择阈值，对小波系数进行阈值操作，得到新的小波系数；

第三，由修正后的小波系数重建得到原始信号。

上述步骤的重点是阈值的选取和阈值函数的确定。阈值的确定是小波收缩消噪最关键的一步，阈值过小，则方差偏大，数据欠平滑；阈值过大，会使数据过平滑，信号的奇异性可能丧失。理由如下：

设S是无噪信号，Xλ是施加阈值后观察信号的小波系数，λ为小波阈值，N为采样长度。则：

偏差：

方差：

由Xλ近似S所产生的“风险（risk）函数”定义为：

可以证明，估计的风险（Risk）为：

Risk=E{R(λ)}=bias2(λ)+var(λ)

当估计的偏差增大时，方差会减小；当偏差减小时，方差会增大。文献［146］证明使Risk达到最小的λ为：

式中：～表示渐进等效（asymptotic equivalence），λMSE称为基于均方误差的最小风险阈值，uσ为噪声的方差，该噪声为零均值的高斯白噪声。由此得到著名的通用阈值：

Donoho和Johnstone证明，阈值的小波非线性估计子是空间自适应的，在Besov空间渐进接近极小极大风险，且具有良好的视觉效应，而不足之处是估计的信号过于平滑。

第二节　基于DT−CWT块阈值的降噪方法

一、基于DWT的NeighBlock块阈值降噪法

尽管VisuShrink阈值法有很强的理论基础［144］，取得了很大的突破和成功，但是它也有其不足之处。它只是在均方误差MSE下获得了方差和偏差的一种平衡或折中，为了尽可能地去除噪声，加大了偏差却减小了方差，而二次偏差在幅值上是一个比方差更高阶的量，所以VisuShrink阈值的结果是过于平滑的，这个问题不可能仅仅通过调节阈值大小来解决，因为这个阈值规则在逐项的统一阈值规则中是渐近最优的［147］。

另外，信号的小波变换展开可以看成是一种信号的稀疏表示，这就是说一个不含噪的信号的信息（或能量）主要集中在少数系数上，如图6.1所示。由图6.1也可看出，大的细节系数几乎都是成块出现，而且主要集中于信号有明显变化的部位。如果在小波阈值估计的过程中考虑邻域的小波系数，可能会提高回归估计的精度。在对此作进一步研究的基础上，Cai等［143］提出了一种基于DWT的NeighBlock块阈值降噪方法。Hall等［107］和Cai等［147～149］研究了小波函数估计的块阈值规则法，这些阈值规则不是逐项地进行阈值操作，而是以块的形式对块内的系数同时进行阈值估计，根据该块的阈值大小来决定该块内的所有系数是整体进行阈值处理还是整体去除。

图6.1　Spikes信号及其小波变换系数

注：S为原始信号，a3为近似系数，d1～d3为细节系数

相对于传统的诸如VisuShrink阈值法等的固定阈值法而言，块阈值法主要有如下改进：

第一，更好的渐近最优性：Donoho等［144，145］提出的软、硬阈值估计子在不计一对数因子时可以达到最优收敛速度，而Hall等［150］或Cai［148］提出的块阈值估计子却可以获得精确的极小化极大收敛速度；

第二，更好的均方误差特性：通过利用邻域小波系数的信息，提高了估计的精度，本章第二节的仿真试验分析用试验说明了这点；

第三，更强的自适应性：块阈值法通过对小波系数进行分块处理，对各个块分别进行阈值操作，相对于传统的诸如VisuShrink估计子的固定阈值而言，明显增加了阈值的自适应性。

1. 非重叠块阈值去噪方法

在每一分解尺度上分割小波系数为各个不重叠的块，根据每一块内小波系数平方和的幅度保留或去掉此块内的小波系数。在高频尺度上，小波系数分割为长度为L的互不重叠的块。假设ss表示块内小波系数的平方和，如果ss比阈值λ=cLN−1σ2大，则此块内所有小波系数进行阈值处理，否则全部抛弃。块阈值估计的性能取决于块长度L和常数c的选择，VisuShrink阈值实际上为块阈值的特例，此时L=1，c=21ogN。Cai［143］系统地研究了块长度L和常数c的选取对块阈值估计的影响，通过选择恰当的参数，块阈值估计子能获得比逐项阈值估计子更为优越的性能（包括风险及渐进性能）。不足之处为块阈值去噪法不是完全数据驱动的，常数c的选取在理论上不是直接给出的，需要借助于一些经验。

2. 重叠块阈值去噪方法

DWT_NeighBlock阈值法是一种重叠块阈值去噪方法［143］，是Cai和Silverman在非重叠块阈值去噪方法基础上于2001年提出的，每一小块的小波系数的取舍取决于重叠大块的小波系数。

在分解尺度j，分割小波系数为不重叠的小块，左右延长每一小块形成互相重叠的大块。在每一小块中，估计小波系数：

其中νj,k为观察信号的小波系数；收缩因子由大块内的小波系数确定。

二、基于DT−CWT的重叠块阈值的降噪方法

通常的离散正交小波变换不能从多角度的尺度很好地匹配信号的局域化性质，无论是采用统一阈值还是极小极大阈值等，在信号的奇异点附近小波收缩估计子存在伪Gibbs现象，去噪后信号在奇异点附近交替出现过冲与欠冲，这不是原始信号固有的，而是去噪过程中小波的局限性导致的。Coifman和Donoho等［151］把这种现象的存在归结为采用的小波变换不具有平移不变性并提出采用“Cycle spinning”方法加以抑制。在一定范围内作循环平移运算，通过改变信号的排列次序即改变信号的奇异点位置，使小波匹配信号奇异点，再平均所得结果，达到降低或消除振荡的目的。其优点是可以在阈值法去噪中有效地去除在信号的不连续点处所产生的伪Gibbs现象，表现出比一般阈值法更好的视觉效果。它的缺点是计算速度很慢。抑制伪Gibbs现象的另外一个更鲁棒的方法是使用具有平移不变性的小波变换，而DT−CWT就具备这种特性。

Cai提出的DWT_NeighBlock法是采用常规的DWT。由于DT−CWT所用到的两个小波变换也分别都是离散正交小波变换，因此本章在此基础上提出一种基于DT−CWT的重叠块阈值的降噪方法DT−CWT_NeighBlock，该方法在DWT_NeighBlock的基础上引进了DT−CWT的平移不变降噪特性，因而可以更好地凸现强噪声背景下的弱信号特征。

方法步骤如下：

第一，将长度为N的被分析信号用DT−CWT分解成M层，得到两棵树的每层的小波系数，按第M层的近似系数LM、第M层的细节系数HM、第M−1层的细节系数HM−1、……第1层的细节系数H1的排列顺序把每棵树的小波系数排成长度为N的系数信号，共得2个系数信号。

第二，对每个系数信号分别进行分块操作得，块长度为L0=[(logN)/2]（符号［］表示取整运算，边界处的块长度取其实际大小），其中i表示所在层数，j表示块序号。近似系数不参与分块也就是不进行阈值处理。

第三，将L0扩展成L=L0+2L1，其中L1=max｛1,[L0/2]｝，得到块。（边界处扩展长度会有不同，但也类似处理）。

第四，对每个块进行阈值操作：

其中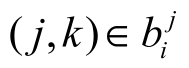，，wj,k为降噪前未处理的小波系数，表示第j块的第k个系数。

而收缩因子：

其中，2σ为噪声方差，阈值常数λ≈10.505 24（该常数由方程λ−logλ=3计算所得［143］）。

第五，将以上两棵树的阈值操作后的系数进行逆DT−CWT，即得降噪后的被分析信号。

例如，当N=1 024，M=3时，其中一个系数信号的排列处理示意如图6.2所示。

图6.2　一个系数信号的排列处理示意图

第三节　试验结果及分析

用两个典型的非平稳信号Doppler信号、Heavisine信号（如图1.5、图1.6中的原始信号）和典型的非线性信号Lorenz信号（如图6.3中的原始信号）以及冲击信号来检验本章方法（DT−CWT_NeighBlock）的有效性。

图6.3　Lorenz信号的原始时域图及其降噪

一、非平稳、非线性信号

Doppler信号、Heavisine信号和Lorenz信号在各方法下得到的信噪比如表6.1所示。这三个染噪信号都是原始信号叠加高斯白噪声。

表6.1　Doppler信号、Heavisine信号、Lorenz信号和冲击信号在各方法下得到的信噪比 单位：dB

Lorenz信号是典型的非线性信号，其原始时域图及其降噪后的信号如图6.3所示。

二、冲击信号

DT−CWT_NeighBlock降噪法不仅能够抑制白噪声，还能去除瞬间出现的脉冲噪声，同时很好地保留有一定持续时间的冲击信号。原始信号及其降噪效果如图6.4所示。经各种方法处理得到的信噪比如表6.1。DWT软阈值法降噪得到的效果明显不如其他方法，故其信噪比在表6.1中未列出。

图6.4（b）中染噪的冲击信号的采样长度为1 024点，该信号除了包含高斯白噪声外，还在第155（约0.15s）、255（约0.25s）、345（约0.33s）、512（约0.5s）、900（约0.88s）点处分别有脉冲噪声。

从表6.1可知：本章提出的DT−CWT_NeighBlock降噪法能够获得比DWT_NeighBlock降噪法更高的信噪比。从图6.4可以看出：块阈值降噪方法不仅能够抑制高斯白噪声，还能有效去除脉冲噪声，同时保留有用的冲击信号，而这是一般的小波降噪方法很难作到的（如图6.4（e））。特别地，从图6.4中约0.32秒处的降噪效果看：本章方法可以更好地保留强噪声背景下（此处有高斯白噪声和强脉冲噪声）的弱信号特征，更好地再现原始无噪信号。

对于旋转机械设备的振动信号，由故障所产生的冲击成分总会持续一定的时间，也就是这种冲击从开始到结束有一个逐渐变大再逐渐变小的过程，而且还是周期性的，这样就跟随机脉冲噪声带来的冲击区别开来，因为这种随机噪声应该总是瞬态的、非周期的。由此可见本章方法对于识别这两种冲击信号是非常有效的而且具有独特优势。

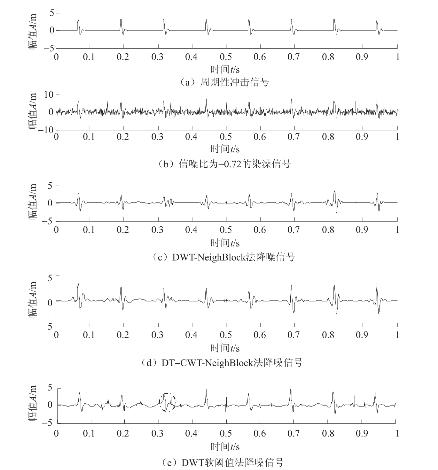
图6.4　染噪的冲击信号的降噪

从图6.4中虚线椭圆即约0.32秒处的降噪效果看，本文介绍的方法可以在强噪声背景下更好地再现原始无噪信号。

三、轧机齿轮箱故障诊断的应用实例

本节以某高线精轧机齿轮箱在线监测系统所采得的现场数据为依据，对轧机齿轮箱的工况进行了深入的分析。

现场数据为26#轧机齿轮箱的振动加速度信号。数据采集时间是2005年01月23日19:54至2005年01月30日08:03（对应图6.5、图6.6中第26个时间点）。

首先，对该轧机齿轮箱振动峰值及均方根值进行了趋势分析，如图6.5、图6.6所示。

图6.5　峰值趋势图

图6.6　均方根值趋势图

由这些趋势图可以看到：26#轧机在2005年01月29日第20个时间点以后的时间里振动的峰值和均方根值都有明显的增大，说明从这一时间开始，齿轮箱的振动能量明显增大。

其次，对该26#轧机进行了进一步的精密诊断。

根据趋势图，可知该轧机出现了异常。为进一步确定故障源，用本章方法作了如下分析。

在该精轧机齿轮箱上测得振动故障信号，图6.7（a）中，采样频率是5 000Hz，采样长度是1 024点。用本章方法作了如图6.7所示的分析。

图6.7　实际齿轮箱故障振动信号的降噪

从图6.7（c）可以看出：在1 024/5 000=0.204 8（秒）的时间内，非常清楚地出现12个冲击，这些冲击所对应的频率为12/0.204 8=58.593 75（Hz）。而该精轧机锥箱I轴的转频（同时也是该轴轴承内圈旋转频率）的理论计算值是58.594Hz，二者完全吻合。最后的检查结果是：该轧机锥箱I轴的轴承内圈损坏（包括磨损），滚珠剥落，导致轴承偏心，当轴旋转时轴心（内圈中心）会绕外圈中心摆动，回转轴每转一周便产生一次振动冲击。

该损坏的轴承的实物图片如图6.8所示。

图6.8　26#精轧机I轴损坏的轴承

由此可见：DT−CWT_NeighBlock法能较好地提取出周期性的冲击特征，而DWT_NeighBlock法（如图6.7（b））及其他方法（如图6.7（d）的DWT软阈值法）不能完整或不能很好地提取出某些冲击特征信号（比如图中虚线椭圆框所示）。

值得一提的是，对于图6.7（d）的DWT软阈值法，取不同的阈值会有不同的结果，图6.7（d）所取的是最接近于图6.7（c）的阈值。当进一步加大阈值时，图6.7（d）中约0.008s、0.041s、0.09s等处的冲击就会消失；当进一步减小阈值时，在结果中就会出现很多类似于图6.7（d）中约0.182s处的随机脉冲噪声。

而对于块阈值法：首先，由式（6.2.1）、式（6.2.2）可以看到，其阈值大小完全是自适应的，根本不需要人为地设定，块长度也是给定的；其次，其分解层数相对固定，DWT_NeighBlock法的分解层数一般是3，DT−CWT_ NeighBlock法的分解层数一般是5；最后，经验证在DT−CWT_NeighBlock方法中选择不同的小波对块阈值法降噪的结果影响不大。因此，块阈值法降噪的结果几乎是唯一的，这点相对于目前常见的小波阈值降噪的方法的众多阈值和小波选择而言，块阈值法更适合机械设备故障诊断的客观判断，其结果更不易受人为的主观因素的干扰。