从头算自洽场（

2.2　从头算自洽场（Ab Initio SCF）方法

除采用分子理论物理模型的三个基本近似，以及LCAO－MO的数学近似之外，不再引入其他近似。遵从这一原则，严格求解分子的Hartree-Fock-Roothann方程，以获得分子波函数及其能级，并利用它们进一步计算分子的其他性质。这样的处理称为从头算法，又称“量子力学第一计算原理”（First principle calculation），或“Hartree-Fock计算”。由于更精确的“Post-Hartree-Fock”处理，以及各种较粗略的半经验量子化学计算方法，均由从头算法派生而来，故从头算法被称为量子化学计算的主流。

我们将在下面对从头算方法的一些基本概念进行简要的介绍。从头算一般是指求解单电子近似下Hartree-Fock方程的理论方法，通常称为分子轨道理论。本书使用的Gaussian 03程序就是基于这一理论框架。

自洽场计算中，体系的波函数可用一个或多个Slater行列式来表示。如给定Hamilton算子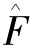，单电子波函数φ_i满足Hartree-Fork方程：

其中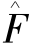为Fork算子，可表述为

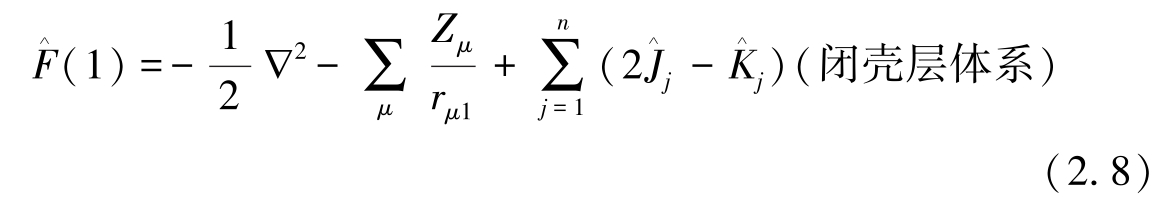
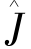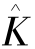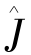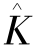上式中和分别是库仑算子和交换算子，和满足：

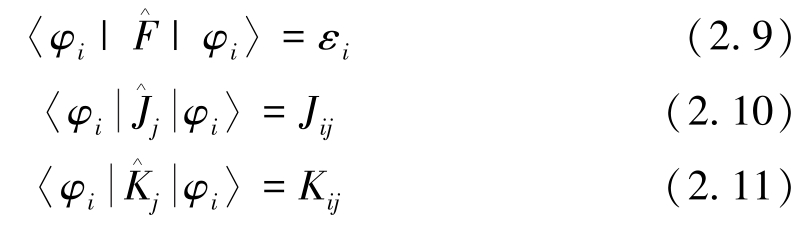
上述（2.8）、（2.9）、（2.10）和（2.11）四式结合，可得

式（2.12）中，分子中的单电子平均动能和单电子与核之间的平均吸引能表述如下：

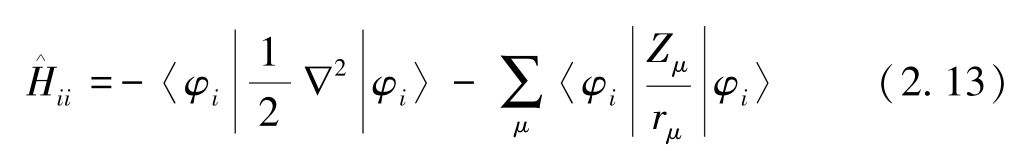
对闭壳层分子来说，由于每个分子轨道包含两个自旋相反的电子，从而可以得到电子总能量为

由于每一个分子轨道的电子能量的计算均是在其他电子的平均作用场下进行，如果简单加和，将会引入两倍的库仑作用及交换作用。因此，分子的电子总能量不是简单的分子轨道能量的两倍。

1928年Roothann提出了一个将N个电子体系中的每一个电子都看成是在由其余的N－1个电子所提供的平均势场中运动的假设。这样对于体系中的每一个电子都得到了一个单电子方程（表示这个电子运动状态的量子力学方程），称为Hartree-Fock-Roothann（简称HFR）方程，使用自洽场迭代方式（Self-Consistent-Field，SCF）求解这个方程，就可得到体系的电子结构和性质。Hartree-Fock-Roothann方程的矩阵表述形式如下：

上式中S和C分别是波函数重叠矩阵和分子轨道线形组合的系数矩阵。HFR方程在形式上是个本征值问题，ε相当于算符F的本征值，C相当于算符F属于本征值ε的本征向量。但是与一般的本征值问题不同的是，由于算符F本身是分子轨道组合系数函数，因此，在解HFR方程时，只能用迭代的方法，即所谓的自洽场（SCF）方法。