四、原子吸收光谱法测定陶瓷中溶出的镉
该方法使用原子吸收光谱仪通过用4%(V/V)醋酸水溶液浸泡测定从陶瓷表面溶出的铅或镉的量。
步骤1:技术规定
英国标准BS6748:1986“陶瓷、玻璃、玻璃—陶瓷和搪瓷器皿中溶出的金属限量”给出了完整的测定程序,并形成被测量的技术规定。图7给出的仅仅是大概描述。
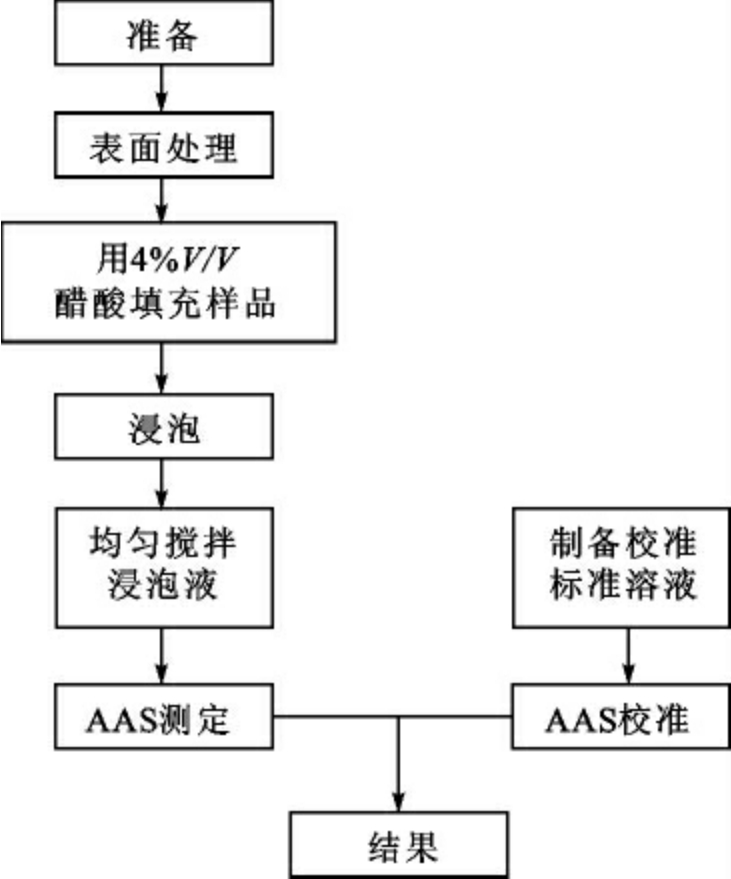
图7 测量过程示意图
1.仪器和试剂的技术规定
影响不确定度的试剂规格:
·新配制的4%(V/V)冰醋酸水溶液,用水将40mL冰醋酸稀释至1升。
·4%(V/V)醋酸溶液中铅标准溶液的浓度为(1000±1)mg·L-1。
·4%(V/V)醋酸溶液中镉标准溶液的浓度为mg·L-1。
实验用玻璃仪器要求至少是B级,并且在测定过程中在4%醋酸溶液中不会溶出可检测到含量的铅或镉。原子吸收光谱仪要求其检测限为:
铅0.2mg·L-1,镉0.02mg·L-1。
2.程序
影响不确定度评估的技术规定:
ⅰ)样品在(22±2)℃的条件下放置,适当时(“类别1”的产品),测量样品的表面积。如在本例中,表面积是2.37dm2。
ⅱ)将(22±2)℃的4%V/V醋酸溶液倒入经预处理的样品中,使溶液填充的高度为距离样品溢出处1mm,可从样品上端边缘处测量。
ⅲ)记录使用4%V/V醋酸溶液的量,精确至±2%(本例使用了332mL醋酸)。
ⅳ)样品在(22±2)℃的条件下放置24小时(测镉时要放置在黑暗中),并采取适当的措施防止挥发损失。
ⅴ)放置后,搅拌溶液使其足够均匀,取一部分测试样,必要时进行稀释(稀释系数为d),选用适当的波长在AA仪器上进行分析,本例中是最小二乘法校准曲线。
ⅵ)计算结果,报告在总浸取液中铅和/或镉的量,对于类别1的产品,用每平方分米表面积含多少毫克铅或镉的方式表示,对于类别2和3的产品,用每升体积含多少毫克铅或镉的方式表示。
步骤2:识别和分析不确定度来源
步骤1描述了“经验方法”。如果这个方法在指定范围内使用,方法的偏差被定义为零。因此偏差的评估与实验室的操作有关,而与方法固有的偏差无关。因为还没有一个有证标准物质用于这个标准方法,偏差的总体控制与影响结果的方法参数的控制有关。这些影响量是时间、温度、质量和体积等。
稀释后醋酸溶液中铅或镉的浓度C0用原子吸收光谱法测定,计算公式如下:
![]()
其中:
C0:在浸取液中铅或镉的浓度[mg·L-1]
A0:浸取液中金属的吸光度
B0:校准曲线的截距
B1:校准曲线的斜率
对于本例所考虑的类别1的产品,经验方法要求结果用每单位面积溶出的铅或镉的质量r来表示,r的计算式如下:
![]()
其附加参数是:
r:每单位面积溶出的铅或镉的质量r[mg·dm-2]
VL:浸取液的体积[L]
aV:容器的表面积[dm2]
d:样品的稀释系数
上述被测量公式的前面部分被用于绘制基本因果图,如图8所示。
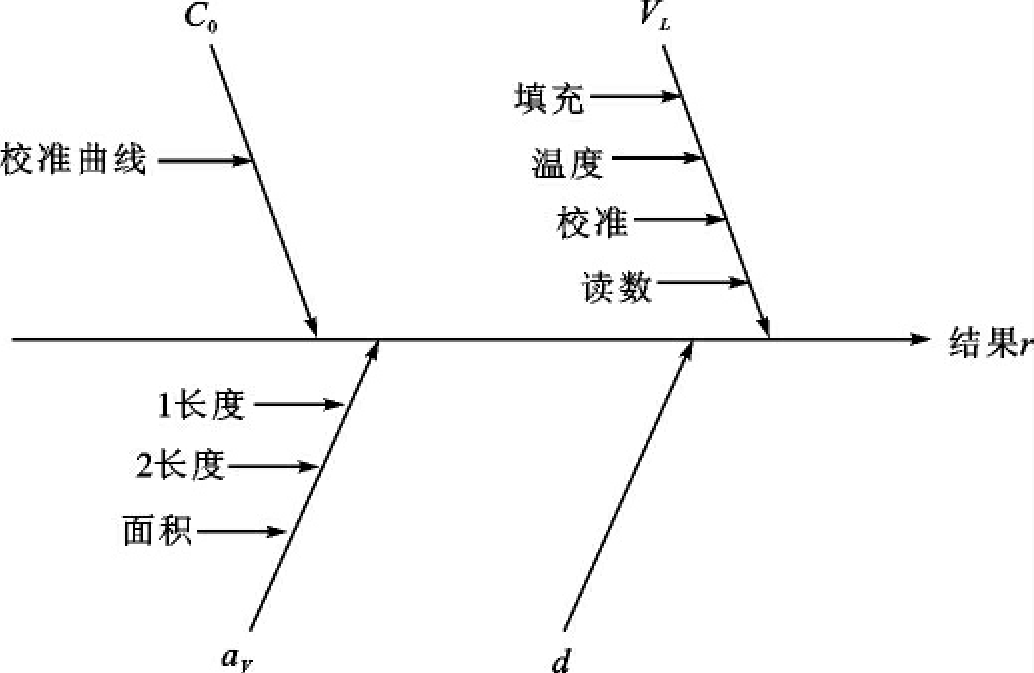
图8 初步因果关系图
对于本经验方法,目前尚无有证标准物质用于评估实验室的操作。因此所有可能的影响量都要考虑,如温度、浸泡时间和酸度。为了考虑附加的影响量,公式中需加入各自的修正因子,因此扩大为:
![]()
这些修正因子包含在已修正的因果图中。
注:该标准所允许的温度范围会引入不确定度,这是由于被测量技术规定不完善而产生。符合经验方法以及实际可行时,考虑温度的影响允许对被报告的结果范围进行评估。尤其要注意由不同操作温度引起的结果变化,因为是在按照技术规定要求测试而得到的结果,因此不能合理地认为是偏差。
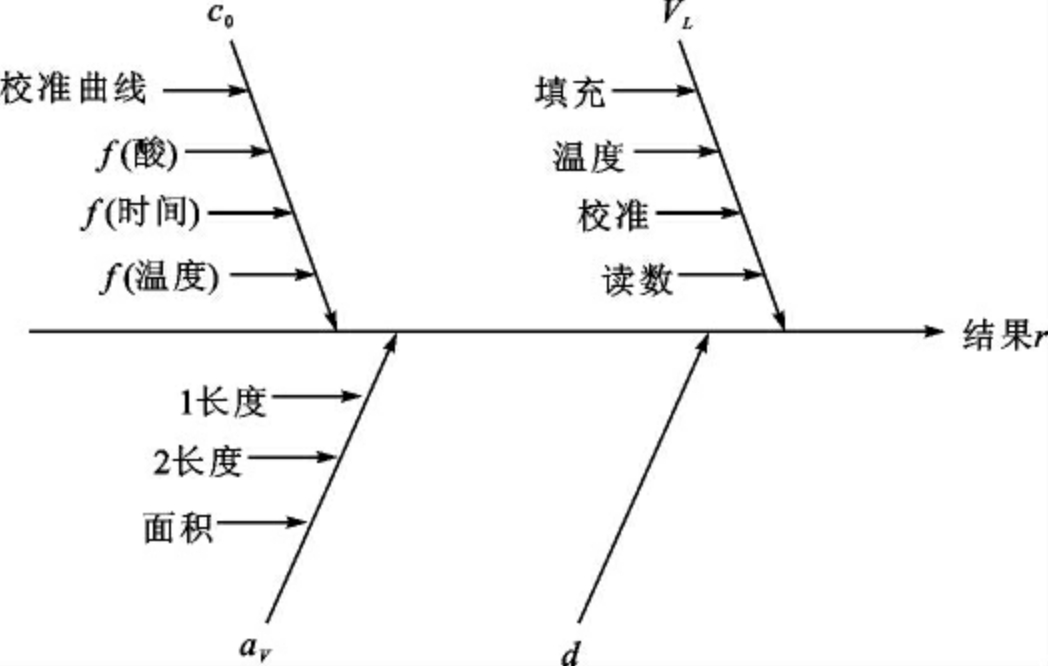
图9 添加了修正因子的因果关系图
步骤3:量化不确定度来源
这个步骤的目的是对先前识别的每一个不确定度的来源进行量化。可以用实验数据或基于良好的假定来进行量化。

,无需稀释浸取液,因此不用考虑其对不确定的影响。
填充体积:经验方法要求容器被溶液填充至“距离边缘1mm以内”。对于典型的饮用和厨房用具,1mm将代表器皿高度的1%。因此容器被填充的体积为99.5±0.5%(即大约是容器体积的0.995±0.005)。
温度:醋酸的温度必须在22±2℃,由于与容器相比液体具有更大的体积膨胀,这个温度范围导致体积测量的不确定度。假定温度分布为矩形分布,则332mL体积的标准不确定度是:
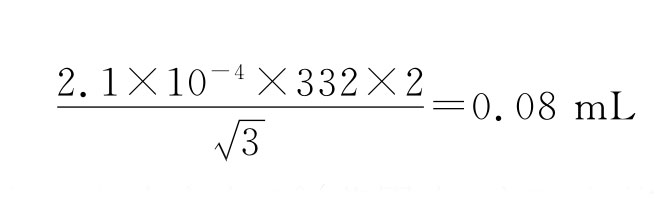
读数:记录体积VL要求的准确度在2%范围内,实际上使用量筒时允许约1%的不准确性(即0.01VL)。假定是三角形分布来计算标准不确定度。
校准:体积校准是根据制造商的技术规格进行的,500mL量筒有±2.5mL的偏差,假设为三角形分布,计算标准不确定度。
本例中体积为332mL,四个不确定度分量按下式合成:
u(VL)=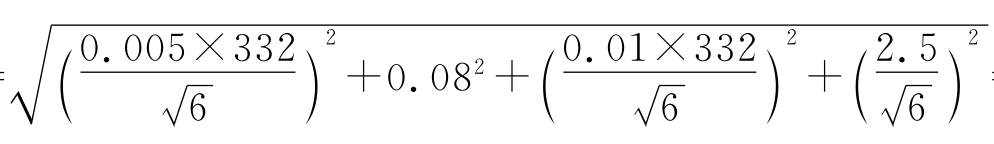 =1.83mL
=1.83mL
镉浓度c0
使用手工绘制的校准曲线计算溶出镉的量。用(500±0.5)mg·L-1镉标准溶液中配制五个标准溶液,其浓度分别为0.1、0.3、0.5、0.7和0.9mg·L-1。使用线性最小二乘法拟合曲线程序的前提是假定横坐标的量的不确定度远小于纵坐标的量的不确定度,因此通常的c0不确定度计算程序仅仅与吸光度不确定度有关,而与校准溶液不确定度无关,也不与从同一溶液中逐次稀释产生必然的相关性。然而在本例中,校准标准溶液的不确定度足够小以至可以忽略。
五个校准标准溶液分别被测量三次,结果见表3。
表3 校准结果
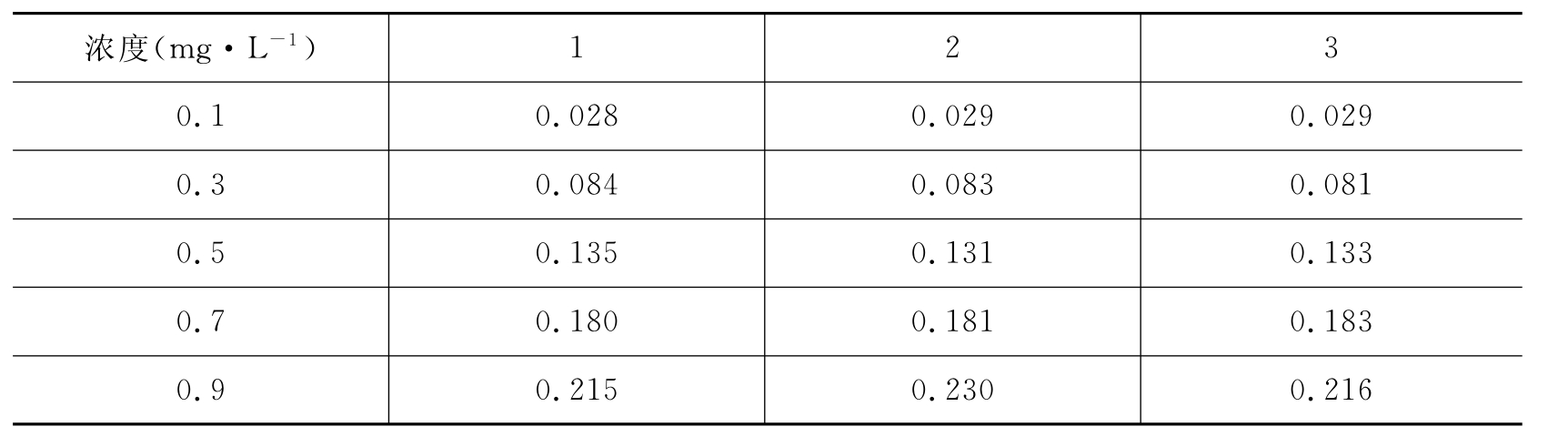
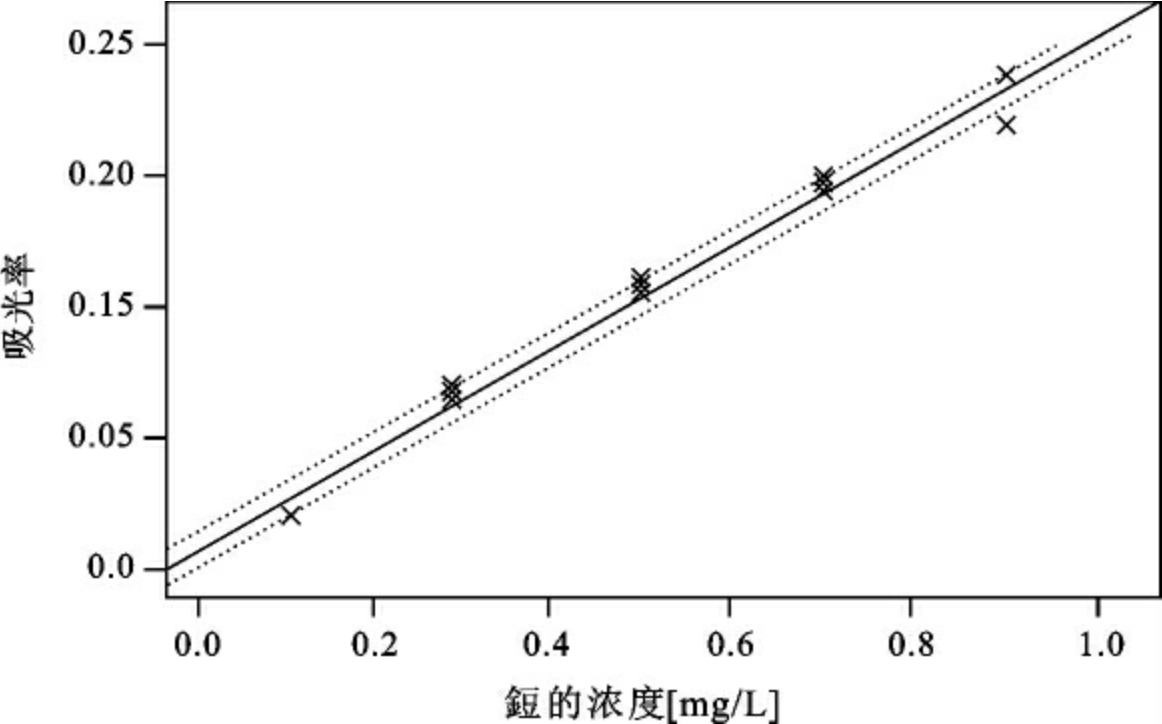
图10 线性最小二乘法拟合和不确定度区间
![]()
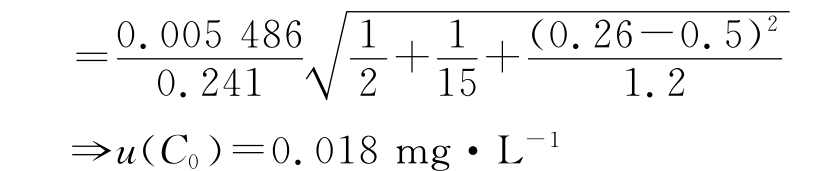
线性最小二乘法拟合曲线的相关系数r为0.997,残余标准偏差S是0.005486。测量浸出溶液两次,浓度c为0.26mg·L-1,残差标准偏差S为:
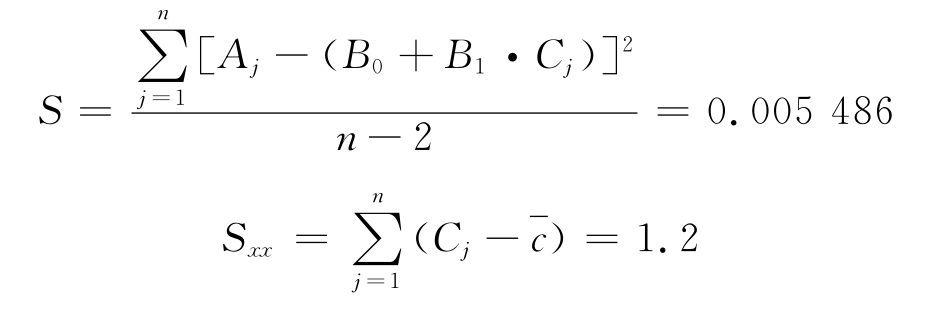
其中:
B:斜率
P:测试c0的次数
n:测试校准溶液的次数(标准系列个数与每个校准溶液测量的次数之积)
C0:浸出液中镉的浓度
c:不同校准标准溶液的平均值(n次)
i:下标,指第几个校准溶液
j:下标,指获得校准曲线的测量次数
面积aV
长度测量:测量样品容器的尺寸计算其总的表面积为2.37dm2,因为样品近似于圆筒但不规则,在95%置信水平中测量偏差估计在2mm范围内。典型的尺寸介于1.0dm和2.0dm之间,其估计的尺寸测量不确定度为1mm(95%的数值除以1.96后)。典型的面积测量需要高和宽两个长度尺寸(即1.45dm和1.64dm)。
面积:由于样品没有完整的几何形状,因此面积计算也有不确定度,在本例中,在95%置信水平时估计有另外5%的分量。
长度测量和面积测量的不确定度分量按通常方式合成。
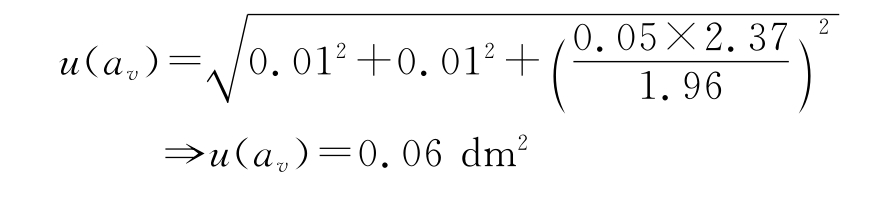
温度影响ftemp
已进行了温度对陶瓷器皿溶出金属影响的一些研究。一般来说,温度影响是相当大的并且随着温度变化,溶出金属呈指数级上升趋势,直至达到极限值。只有一个研究给出20℃~25℃温度范围的影响。从图形资料上看,在接近25℃的温度附近金属溶出量随温度的变化近于线性,其斜率约为5%℃-1。经验方法允许±2℃的范围导致温度系数ftemp为1±0.1。假定为矩形分布,将其转换为标准不确定度:
![]()
时间影响ftime
对于相对较慢的过程,如浸泡过程,溶出量将大约与时间的微小变化成正比。Krinitz和Franco发现在浸泡过程的最后6个小时中浓度的平均变化在86mg·L-1时大约是1.8mg·L-1,即约占0.3%/小时,因此对于(24±0.5)小时的浸泡时间。C0需要用系数ftime进行修正:1±(0.5×0.003)=1±0.0015。
这是矩形分布,产生的标准不确定度为:
![]()
酸浓度facid
有一个研究酸浓度对铅溶出影响的结果显示,当浓度从4%改变为5%(V/V)时,某一特定批陶瓷的铅溶出量从92.9变为101.9mg·L-1,f变为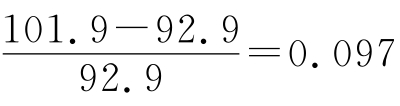 或近似0.1。而另一个研究使用热浸泡方法,结果显示类似的变化(浓度从2%变为6%V/V时,铅含量有50%的改变)。假定这个影响近似于与酸浓度成线性,估计酸浓度的每变化1%(V/V),facid约有0.1的变化。在另一个实验中,使用标准NaOH滴定的滴定法建立了该酸浓度和它的标准不确定度(3.996%V/V,u=0.008V/V)。采用该酸浓度的不确定度为0.008%V/V,则facid的不确定度为0.008×0.1=0.0008,因为该酸浓度的不确定度已表示为标准不确定度,这个值可被直接作为与facid有关的不确定度。
或近似0.1。而另一个研究使用热浸泡方法,结果显示类似的变化(浓度从2%变为6%V/V时,铅含量有50%的改变)。假定这个影响近似于与酸浓度成线性,估计酸浓度的每变化1%(V/V),facid约有0.1的变化。在另一个实验中,使用标准NaOH滴定的滴定法建立了该酸浓度和它的标准不确定度(3.996%V/V,u=0.008V/V)。采用该酸浓度的不确定度为0.008%V/V,则facid的不确定度为0.008×0.1=0.0008,因为该酸浓度的不确定度已表示为标准不确定度,这个值可被直接作为与facid有关的不确定度。
注:原则上,不确定度值需要对上述单个研究是足够代表所有陶瓷情况的假定进行修正,当然,目前的数据已给出了对不确定度数量的合理评估。
步骤4:计算合成标准不确定度
假定没有稀释,则单位面积镉溶出量为:
r=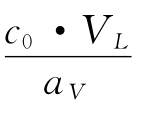 ·d·facid·ftime·ftempmg·dm-2
·d·facid·ftime·ftempmg·dm-2
中间值和标准不确定度被收集于下表,将这些数据代入;
r=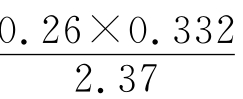 ×1.0×1.0×1.0=0.036mg·dm-2
×1.0×1.0×1.0=0.036mg·dm-2
合成标准不确定度,将标准不确定度的每个分量代入下式:
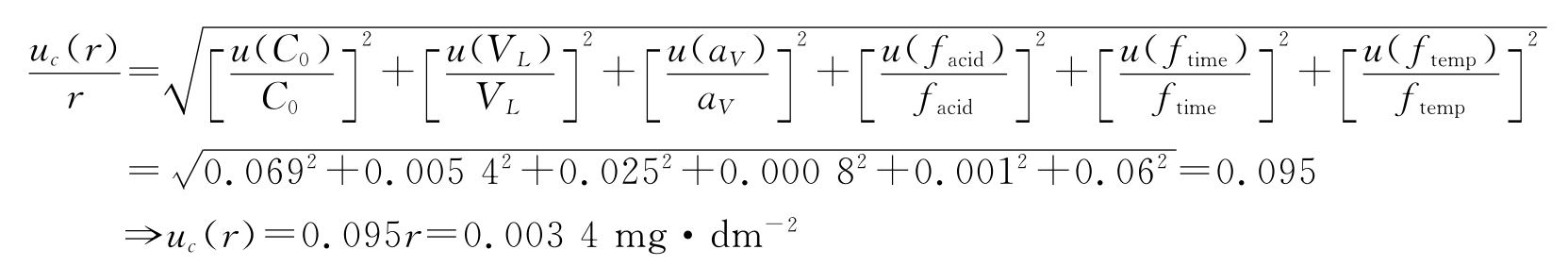
表4 测定镉溶出量的不确定度
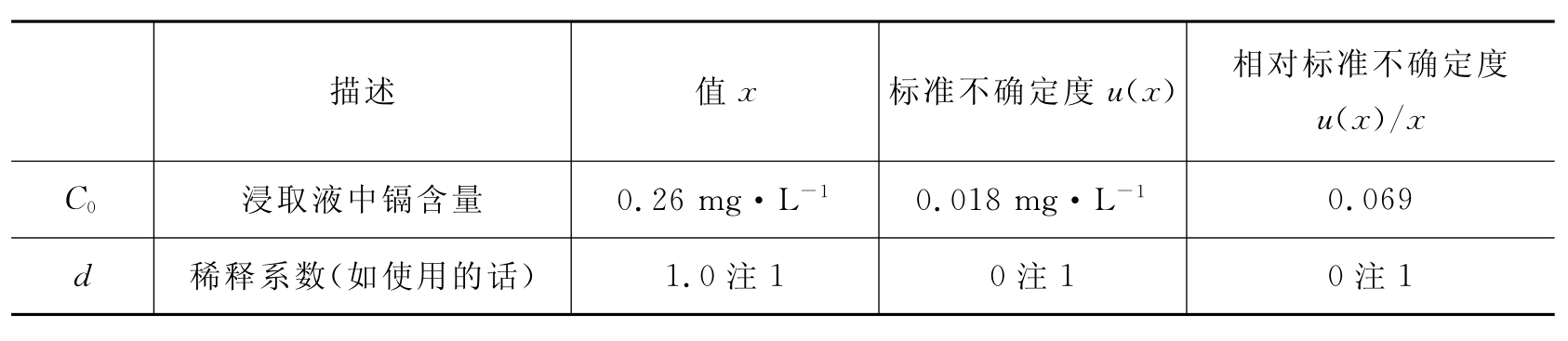
(续表)
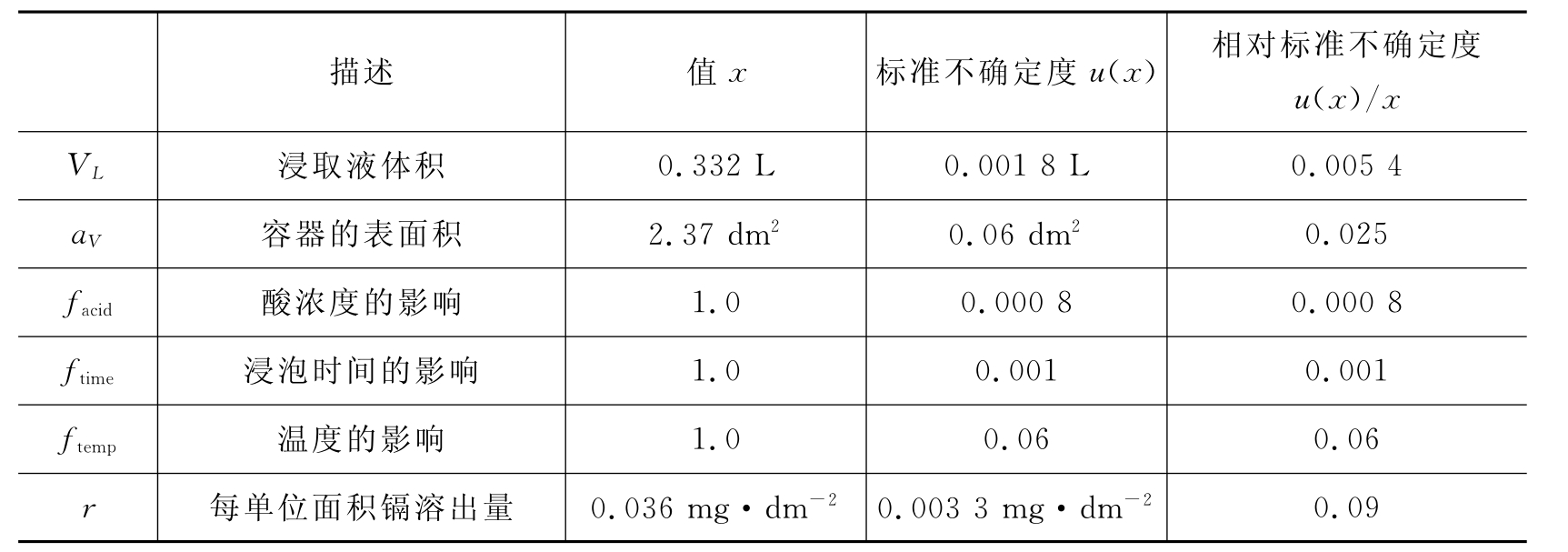
注1:本例中没有用到稀释。因此d正好为1.0。
扩展不确定度U(r)通过使用包含因子2计算得到:Ur=0.0034×2=0.007mg·dm-2
因此按照BS6748:1986标准测量镉溶出量为:(0.036±0.07)mg·dm-2
上述不确定度计算使用的包含因子为2。
图11显示了不同参数和影响量对测量不确定度的贡献。
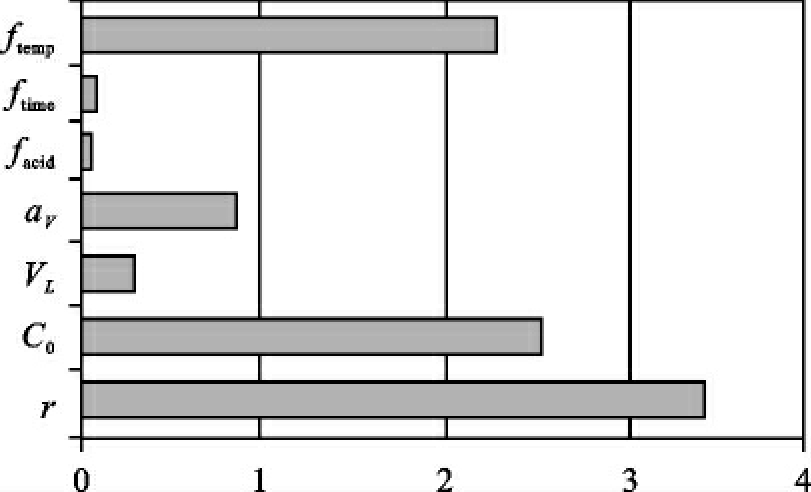
图11 溶出镉测定的不确定度
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















