最速下降线

最速下降线

Brachistochrone

伽利略在1630年提出一个问题：“一个质点在重力作用下，从一个给定点到不在它垂直下方的另一点，如果不计摩擦力，问沿着什么曲线滑下所需时间最短？”他说这曲线是圆，可是这是一个错误的答案。瑞士数学家约翰.伯努利在1696年再次提出这个最速下降线的问题（problemofbrachistochrone），征求解答。次年已有多位数学家得到正确答案，其中包括牛顿、莱布尼兹、洛必达和伯努利家族的成员。这个问题的正确答案是连接两个点上凹的唯一一段旋轮线。

图1　最速下降线演示仪

实验装置

本演示仪器有三条固定的轨道：一条直线、一条任意曲线和一条下凹的摆线，摆线看上去似乎是最长的。这三条轨道的起点和终点是完全相同的，如图1所示。

现象观察

把三个球分别放在三条轨道顶端的挡板前，用手拿开挡板，三球从顶端同时下滑。结果表明，虽然下凹曲线轨道的路线最长，但沿着它下降的球反而最先到达终点。

现象解密

物体沿轨道下降的速度不仅取决于轨道的长度，而且还与轨道的形状有关。重力的作用使三个球下落，球所受重力沿运动轨迹切线方向的分量越大，下落的速度就越快。而摆线轨迹是一条圆滚曲线，重力在它陡峭的切线方向上的分量比较大，球下落速度比较快，先到达终点；而直线和另一条曲线的轨道虽然短，但球下落的速度较摆线上的球慢，后到达终点。

那么，这条最速下降线的轨迹又是什么呢？

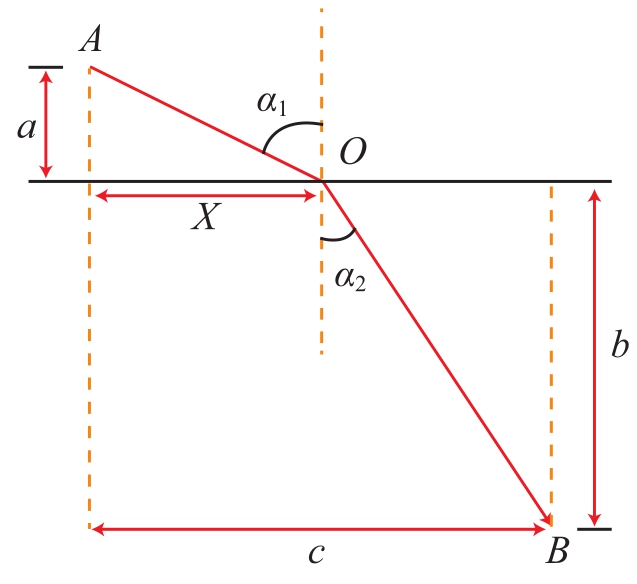
图2　A、B固定的折线路径

假设球与轨道间无摩擦力，球下落的运动路径为如图2所示的AOB。若小球由A到O的速度是V₁，由O到B的速度是V₂，则从A到B所花的时间：

所花时间最短，需取极值，即满足

由此可得

如果路径变成如图3的折线，

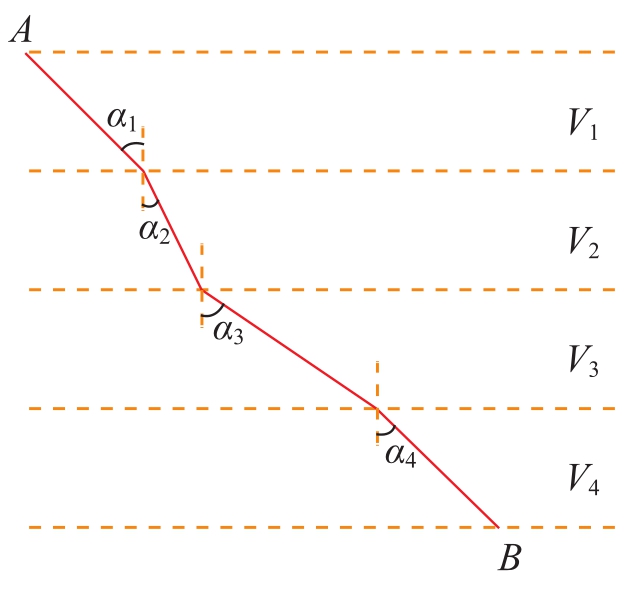
图3　A、B固定的多折线路径

因为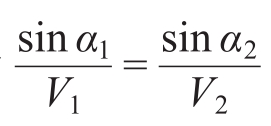

同理可得

所以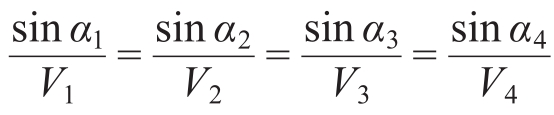

如果将A、B之间的路径越折越多，即越切越细，则可以发现，在每一点会有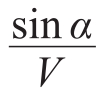=k，这里k为常数。

又因为每一点的V=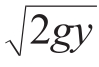，这里取y向下为正，如图4所示。

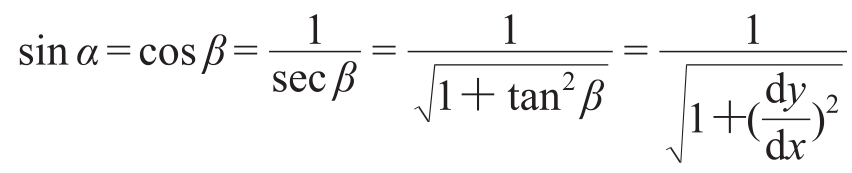
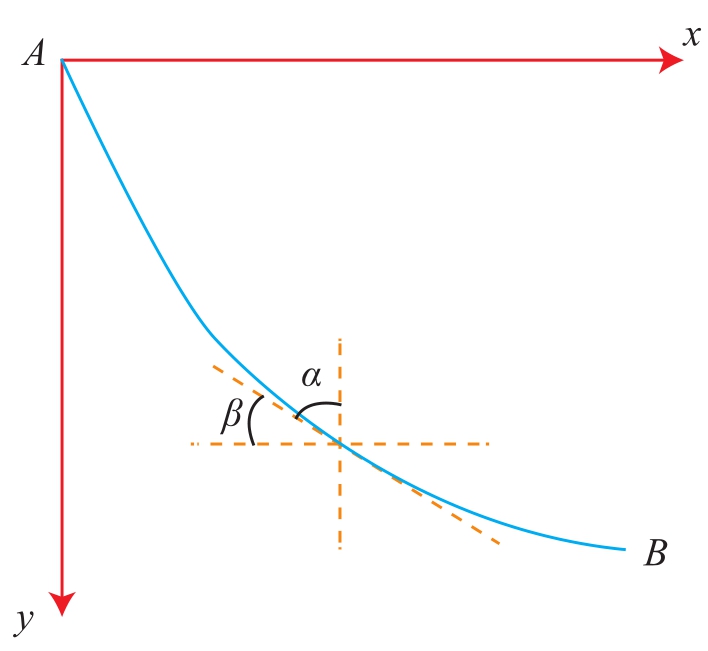
图4　A、B固定的曲线路径

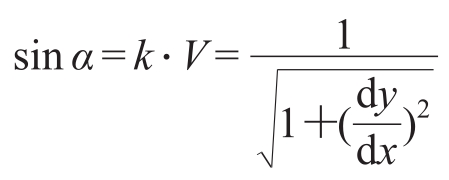
得

由此可得

其中c为常数。

令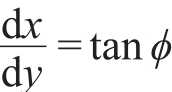

可得

因此

积分得

由初始条件

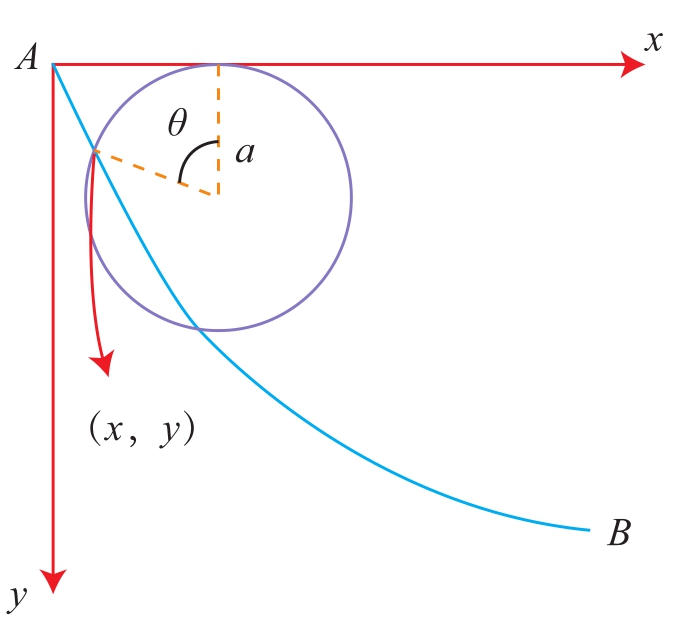
图5　旋轮线

所以c₁=0

代入得

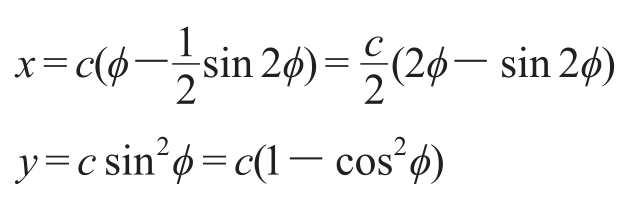
再令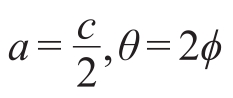

最后得

这是旋轮线方程，如图5所示。因此结论是：最速下降线的轨迹是旋轮线。

知识拓展

当一个圆沿着一条直线滚动时，圆边上一点的轨迹叫做旋轮线或摆线。摆线具有很重要的性质：等时性。即若一质点从一段摆线任意点出发，在重力作用下沿摆线向下滑，则此质点到达最低点所需的时间与出发点的位置无关。摆线另一有趣的性质是：质点在重力场中沿着摆线从高处某一点滑到低处的另一点所用的时间，比沿着任何曲线（包括直线）在同样两点间滑下的时间都短。所以摆线也称为最速下降线。

这个解答所蕴含的基本观点的发展，导致了一门新学科——变分学的产生。欧拉从现实生活中的极大、极小问题提炼出数学问题和解题技巧，创立了“变分学”这一新的数学分支。要得到最速下降线问题的完备解答，需要用到变分学的知识。

思考题

1.最速下降线轨道的参数方程是什么？

2.你能够运用变分学知识，求出质点在重力作用下，从一个给定点到不在它垂直下方的另一点的最快时间吗？

3.在骑自行车的时候，车轮上粘着一张糖纸，糖纸的运动轨迹就是最速下降线的轨迹，为什么？