角动量守恒

角动量守恒

Conservation of Angular Momentum

我们经常能看到，花样滑冰运动员在比赛中做一些原地旋转动作时，为了尽可能地增加自己的旋转角速度，一般都要把胳臂和腿紧紧地收起来。这是为什么呢？本实验将体验刚体定轴转动系统中旋转角速度与转动惯量间的关系。

实验装置

实验装置为如图1所示的茹科夫斯基转椅。

图1　茹科夫斯基转椅

图2　旋转角速度与转动惯量间关系演示实验照片

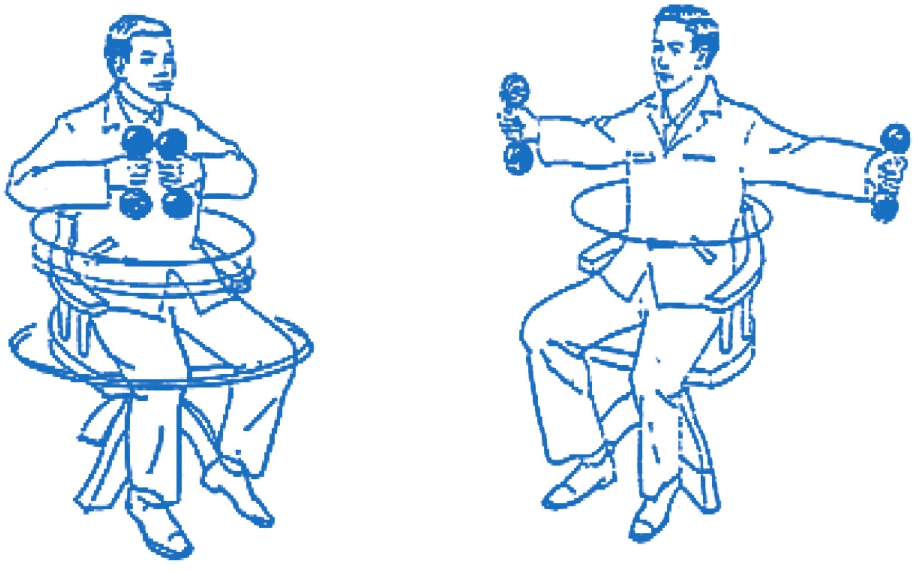
图3　旋转角速度与转动惯量间关系演示示意图

现象观察

实验参与者坐在转椅上，系好安全带，双手握紧哑铃放在胸前，手持哑铃的实验者与转椅构成一个刚体定轴转动系统，如图2和图3所示。另一人推动转椅，使其以一定的角速度转动，实验者也可自己用脚蹬地获得转速，使转椅的转速提高。

1.当转椅转速较高时，实验者将双手举平，使系统转动惯量增大，可观察到轮椅转速减缓。

2.实验者将两手收回胸前，则系统转动惯量减小，转动明显加快。

3.接着，实验者两臂再度平伸，发现转椅的转速又减慢。如此多次重复，直至停止。

现象解密

刚体绕定轴转动的转动惯量为

其中r_i为质量元m_i绕轴的转动半径。转动惯量是刚体转动惯性的量度，转动惯量的大小，反映了刚体转动状态改变的难易程度。

刚体绕定轴转动时，对定轴的角动量为

根据刚体定轴转动的规律

当系统受到的合外力矩为零时，系统的角动量守恒，即

这就是刚体定轴转动的角动量守恒定律。从④式可见：

（1）当刚体的转动惯量J为常量时，若Jω不变，则ω不变，即刚体在不受合外力矩时将维持匀角速度转动。

（2）若转动物体是一种可变形固体，其质量分布在内力的作用下发生了变化，并改变它对转轴的转动惯量，则物体的角速度就会产生相应的变化：当J增大时ω就减小，J减小时ω就增大，从而保持乘积Jω不变，即系统总角动量保持守恒。

应用拓展

做旋转动作中的花样滑冰运动员可近似地看成一个刚体，其所受的合外力矩M约等于零，即此时刚体的角动量L=Jω不变。要使运动员一次性原地旋转角度越大，就要使他做定轴转动的角速度ω越大，由角动量守恒定律可知，必须减小转动惯量J。

由转动惯量的定义式(1)可知，在刚体质量m一定的情况下，转动惯量J的大小由刚体质量的分布情况确定。所以，花样滑冰运动员通过收紧自己的胳臂和腿来缩小自身的质量分布，减小自身的转动惯量J，从而增大角速度ω，达到增加旋转角度的目的。

思考题

1.本实验中，如果实验者双手不握哑铃，光靠收拢和伸张双臂来体验转速的变化，结果与手握哑铃时有何差别？为什么？

2.将一个生鸡蛋和一个熟鸡蛋放在桌上旋转，你能分辨出哪个是生鸡蛋，哪个是熟鸡蛋吗？判别的依据是什么？

3.在本实验中，将转椅上的操作者、哑铃和转椅看成一个系统，其总动能是否发生变化？

4.高台跳水运动员在空中完成空翻两周或三周等动作时，为什么要团身？当运动员快要入水时，身体则必须舒展开来，这又是为什么？