双光栅测量微弱振动位移量

实验18　双光栅测量微弱振动位移量

【实验目的】

（1）熟悉一种利用光的多普勒频移形成光拍的原理，测量光拍拍频；

（2）应用双光栅微弱振动测量仪测量音叉振动的微振幅；

（3）了解精确测量微弱振动位移的一种方法。

【实验仪器】

双光栅微弱振动测量仪（包括激光源，信号发生器，频率计等部分），双踪示波器。

【仪器介绍】

激光器发出的光波波长为635nm，其功率可在0～3mW中调节。

信号发生器的频率范围为100～1000Hz，0.17Hz微调，0～500mW输出。频率计为（1～999.9Hz）±0.1Hz。

音叉谐振频率为500Hz左右。

双光栅微弱振动测量仪面板结构图如图4-18-1所示。

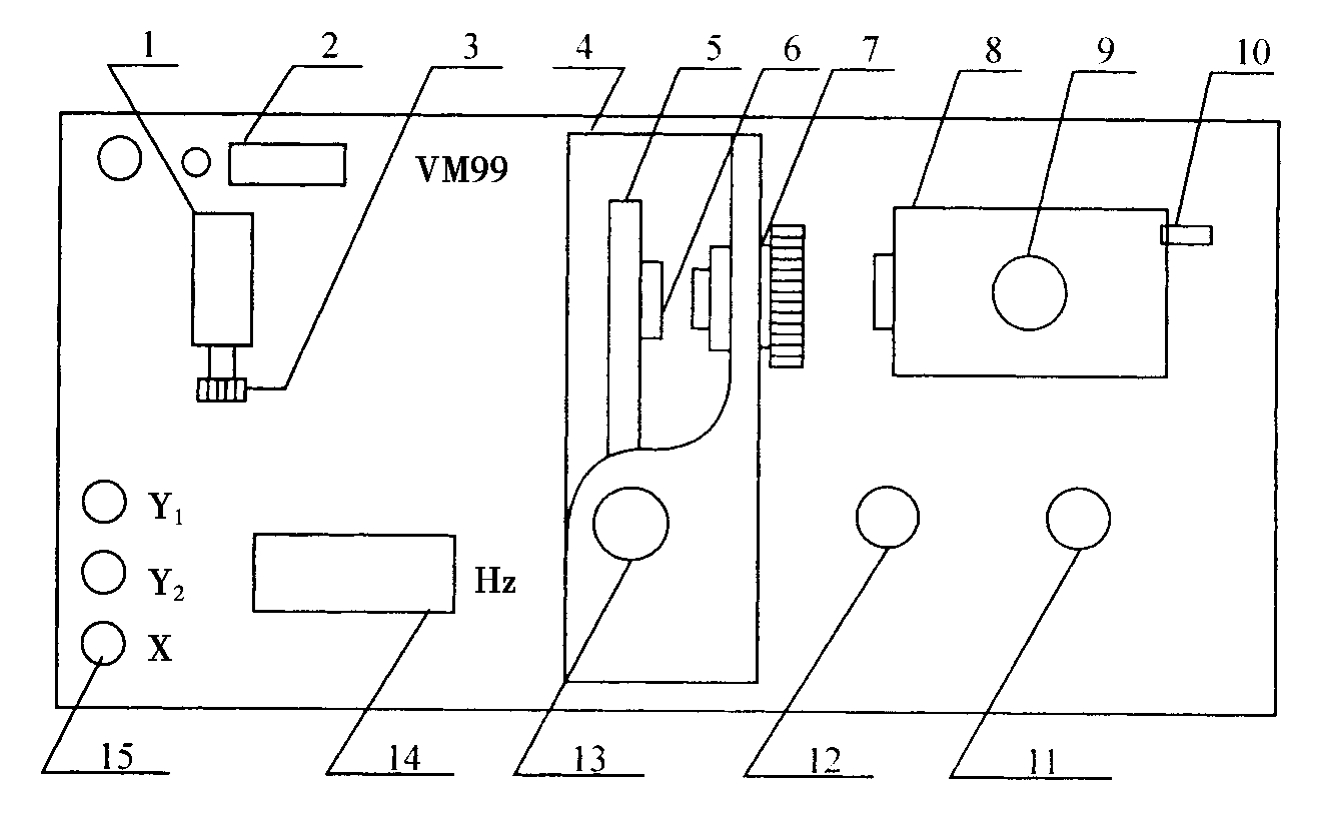
图4-18-1　双光栅微弱振动测量仪面板结构

1-光电池座　（在顶部有光电池盒，盒前有一小孔光阑）　2-电源开关　3-光电池升降手轮　4-音叉座

5-音叉　6-粘于音叉上的光栅　（动光栅）　7-静光栅架　8-半导体激光器　9-锁紧手轮　10-激光器输出功率调节　11-信号发生器输出功率调节　12-信号发生器频率调节　13-驱动音叉用耳机

14-频率显示窗口　15-三个输出信号插口（Y₁拍频信号，Y₂音叉驱动信号，X为示波器提供“外触发”扫描信号，可使示波器上的波形稳定）

【实验原理】

1.位移光栅的多普勒频移

在电磁波的传播过程中，由于光源和接收器之间存在相对运动而使接收器接收到的光的频率不同于光源发出的光的频率，这种现象称为多普勒效应，由此产生的频率变化称为多普勒频移。

理想的单色光在不同介质中的传播速度是不同的，在折射率为n的介质中，光传播的速度是真空中光速的1/n。对于两束相同的单色光，如果初始时刻相位相同，其中一束光在真空中经过几何路程L，另一束光在折射率为n的介质中经过几何路程为L′＝L/n，则经过之后两束光的相位仍然相同；如果初始时刻相位相同，经过相同几何路程而不同折射率的介质，出射时两光的相位则不相同。对于位相光栅而言，当激光平面波垂直入射到位相光栅时，由于光栅上不同折射率的介质对光波的相位延迟作用不同，使入射的平面波在出射时产生了一定的相位差，平面波阵面变成了褶曲波阵面，如图4-18-2所示。

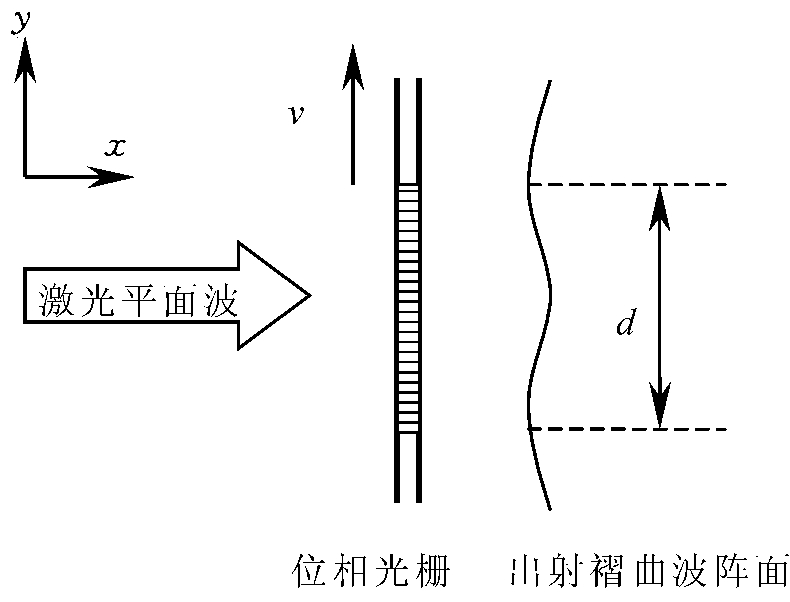
图4-18-2　出射的褶曲波阵面

当激光平面波垂直入射到光栅时，由于光栅上各缝之间的干涉和每缝自身的衍射作用，通过光栅后光的强度呈现周期性的变化。在远场，衍射光线的主极大位置可用如下光栅方程来表示：

式中d为光栅常数，θ为衍射角，λ为光波波长，k为特定的级数。

如果光栅在y方向以速度v移动着，从光栅出射的光的波阵面也以速度v在y方向移动。因而在不同时刻，对应于同一级的衍射光线，它从光栅出射时，在y方向也有一个vt的位移量，见图4-18-3。

这个位移量相应于出射光波相位的变化量为

将式（4-18-1）代入式（4-18-2）得：

式中ω_d＝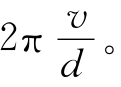

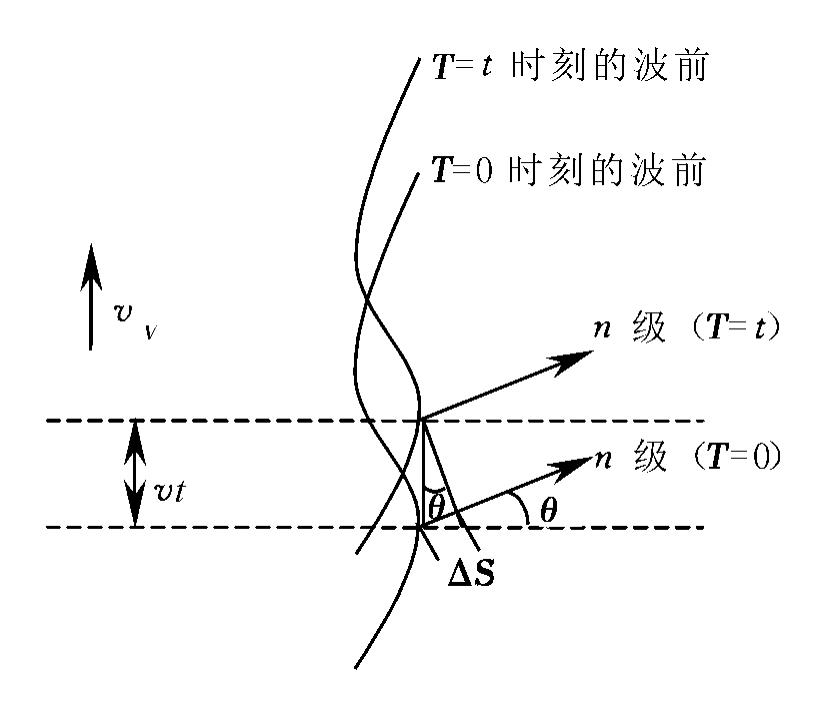
图4-18-3　衍射光线在y方向的位移量

若激光从一静止的光栅出射时，电矢量为

E＝E₀cosω₀t

则光从相应的移动光栅出射时，光波的电矢量为

显然，移动的光栅的k级衍射光波，相对于静止的光栅有一个多普勒频移，其表达式为：

见图4-18-4所示。

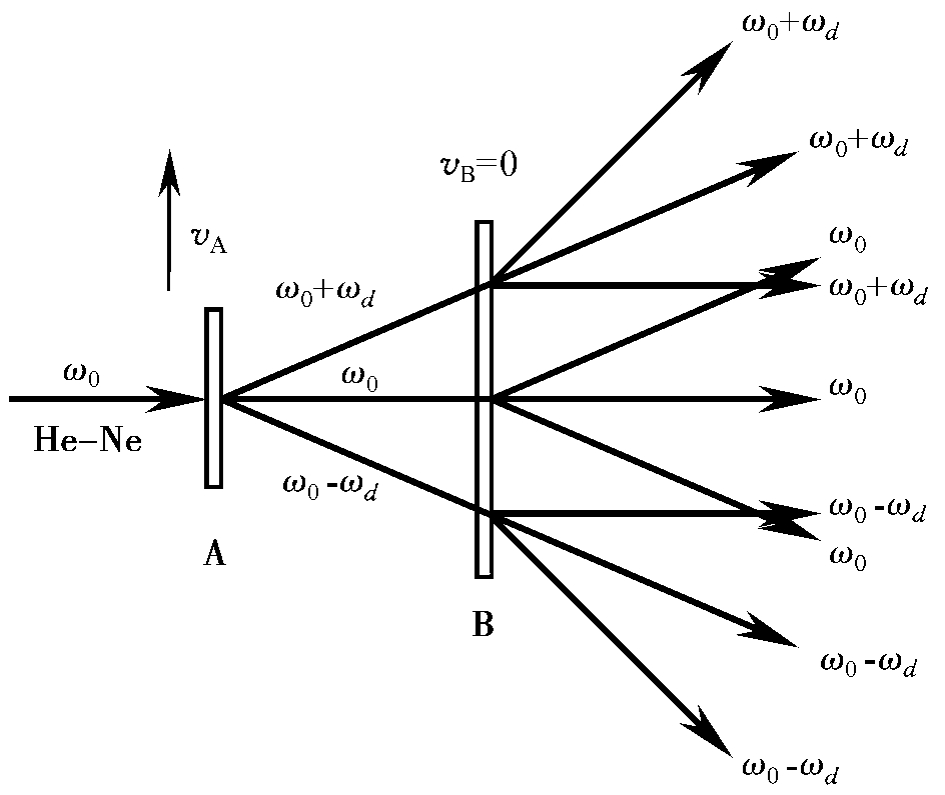
图4-18-4　k级衍射光波的多普勒频移

2.光拍的获得与检测

光的频率非常高，达到10₁₄Hz。到目前为止，即使是最好的光电探测器，其响应时间也远大于光波的周期。为此必须使频差较小的两列光波叠加形成“拍”，由于拍频较低，从而可以检测出多普勒频移量。

将两片完全相同的光栅平行紧贴，其中一片B静止不动（起衍射作用），另一片A相对B按速度v_A移动（起频移作用）。激光入射双光栅后，出射的衍射光包含了不同频率而又平行的光束。由于双光栅紧贴，激光束具有一定宽度，因此该光束能平行迭加，这样就可以直接而又简单地获得光拍，如图4-18-5（b）所示的虚线即为光拍信号。

图4-18-5　频差较小的两列光波叠加形成“拍”

双光栅的衍射光叠加时所形成的光拍信号，进入光电检测器后，其输出光电流可由下述关系求得：

设光束1的电矢量为：E₁＝E₁₀cos（ω₀t＋φ₁）

光束2的电矢量为：E₂＝E₂₀cos［（ω₀＋ω_d）t＋φ₂］

则光电流：

I＝ξ（E₁＋E₂）₂

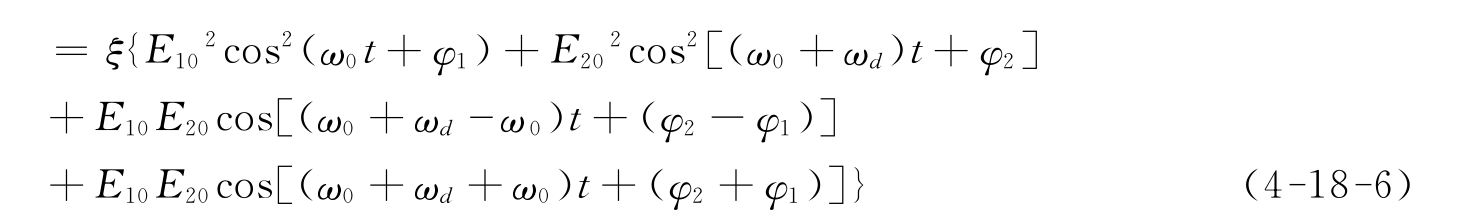
（其中ξ为光电转换常数）

因为光波频率ω₀非常高，对于上述式中的第一、二、四项，光电检测器所产生的光电流只能是在其响应时间内的时间平均值。上式中的第三项是拍频信号，它的频率较低，光电检测器能作出相应的响应。其光电流为

拍频F_拍即为

其中n_θ＝1/d为光栅密度，本实验n_θ＝1/d＝100条/mm。

3.微弱振动振幅的检测

从（4-18-7）式可知，F_拍与光频率ω₀无关。而且当光栅密度n_θ为常数时，F_拍只正比于光栅移动速度v_A。如果把光栅粘在音叉上，则v_A会呈周期性变化。所以光拍信号频率F_拍也随时间变化，音叉微弱振动的振幅为：

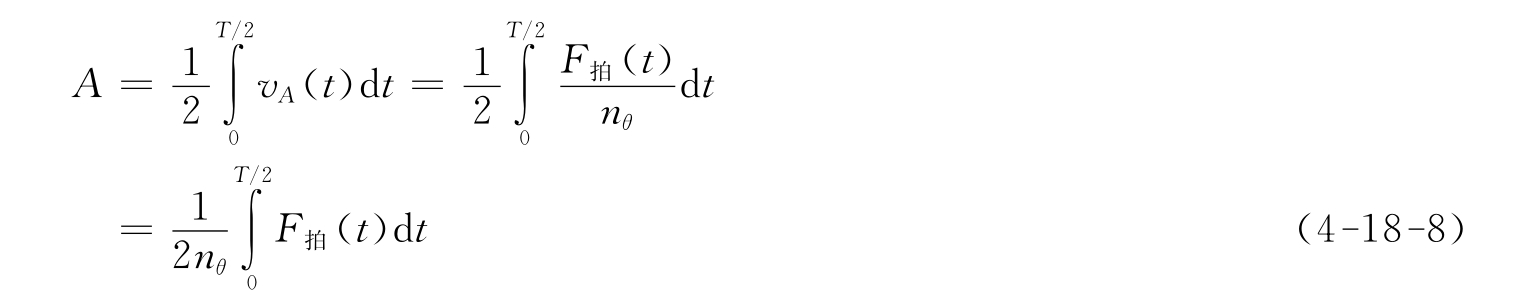
式中T为音叉的振动周期。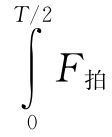（t）dt表示在T/2时间内拍频波的个数。因此，只要测得波数，就可以得到振幅。

在示波器的显示屏上，拍频波的波形数，由完整波形数、波的首数、波的尾数三部分组成。对于屏上显示的不足一个完整波形的首数及尾数，需在波群的两端，按反正弦（或余弦）函数折算为波形的分数部分，即

式中，a、b为波群的首、尾幅度和该处完整波形的振幅之比（波群指T/2内的波形）。

【实验内容】

（1）将双踪示波器的Y₁、Y₂、X外触发输入端接至双光栅微弱振动测量仪的Y₁、Y₂、X的输出插座上，开启各自的电源。

（2）几何光路调整。小心取下“静光栅架”，稍微松开激光器顶部的锁紧手轮，用手小心地上下左右扳动激光器，让光束从安装静止光栅架的孔中心通过。调节光电池架手轮，让某一级衍射光正好落入光电池前的小孔内。锁紧激光器。

（3）双光栅调整。小心地装上“静光栅架”，静光栅尽可能与动光栅接近，注意不能让它们相碰！用一观察屏（或白纸）放于光电池架处，慢慢转动光栅架，仔细观察调节，使得两光束尽可能重合。去掉观察屏，轻轻敲击音叉，调节示波器，配合调节激光器输出功率，就看到拍频波。

（4）音叉谐振调节。先将“功率”旋钮置于6～7点钟附近，调节“频率”旋钮（500Hz左右），使音叉谐振。调节时用手轻轻地按音叉顶部，找出调节方向，如音叉谐振太强烈，将功率旋钮向钟点减小的方向转动，使在示波器上看到的T/2内光拍的波数为15个左右。自拟表格记录此时音叉的振动频率、屏上完整波的个数、不足一个完整波形的首数及尾数值、以及相应此处的完整波形的振幅值。

（5）测出外力驱动音叉时的谐振曲线。固定“功率”旋钮位置，在音叉谐振点附近，小心调节信号发生器的“频率”旋钮，测出音叉的振动频率与对应的振幅大小，记录下数据。

【数据处理】

（1）求在音叉共振点振动周期内光拍信号的平均频率；

（2）求出音叉在共振点时作微弱振动的位移振幅；

（3）在坐标纸上画出音叉的频率-振幅曲线。

【注意事项】

（1）调整几何光路时应十分小心，取下“静光栅架”时注意不可擦伤光栅。

（2）装“静光栅架”时，应尽可能与动光栅接近，注意不可相碰！

（3）测量音叉的频率—振幅曲线时，不能改变信号功率。

预习思考题

如何判断动光栅与静光栅的刻痕已经处于平行？

思　考　题

（1）测量音叉的频率—振幅曲线时，为什么不能改变信号功率？

（2）本实验所采用的测量方法有什么优点？