神奇的黄金分割的发现

神奇的黄金分割的发现

“黄金”象征着贵重，黄金分割有着广泛的应用。毕达哥拉斯学派对五星图怀有特别的敬意，他们把五星图作为学派的章。传说，他们有条“帮规”，凡毕氏学派成员都要佩带五星图的纪念章，人们推测，可能是因为他们掌握了正五边形和五星图的作图方法引以自豪。

毕氏学派在研究五星图的过程中，发现了五星图的一种奥秘:在正五边形中，相邻顶点的两条对角线(也就是五星图的两条边)互相将对方分割成一长一短两部分，它们满足一种和谐的关系式:

全线段:较长的=较长的:较短的，而且较长的一段正好等于正五边形的边长。

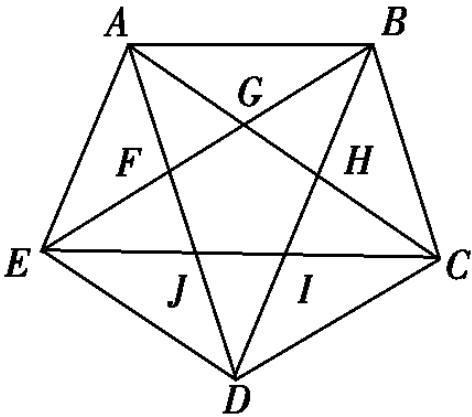
如图:AC与BE相交于G，互相将对方分割成一长一短两部分，我们不难看出:

等腰△AEB～等腰△FEA

∴EB∶EA=EA∶EF

又因为EA=EG，EF=GB

∴EB∶EG=EG∶GB

同理可证CA∶CG=CG∶GA

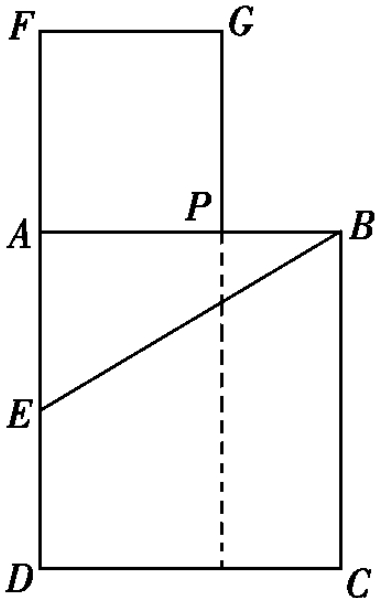
这样，毕氏学派发现了线段的一种“奇妙分割”法，如图，在线段AB上取一点P，把AB分成AP、PB两段，且满足

AB∶AP=AP∶PB

他们采用如下几何方法将线段AB进行这种分割:

以AB为一边作正方形ABCD(如图)，取AD的中点为E，延长DA至F，使EF=EB。作正方形AFGP，则点P即为所求的“奇妙分割”的分点(读者不难自己证明)。

数学史家推测，毕氏学派画五星图就是以这种“奇妙分割”作依据的。

大约在毕达哥拉斯之后150多年，古希腊数学家欧多克斯深入研究了上述“奇妙分割”。欧多克斯是柏拉图的学生，对天文、几何、医学和法律等方面都做出不少贡献。在数学方面，他最大的功劳是，创立了比例论。欧几里得《几何原本》第五卷《比例论》大部分是引用了欧多克斯的成果。欧多克斯的比例论完全排除了毕达哥拉斯的限制，把可公度线段的比与不公度线段的比都包括在内。他从比例论的角度研究毕氏学派的“奇妙分割”，并把这样分割中较短线段与较长线段之比叫做“中外比”。因为点P将AB分成两部分，其中较长部分是全线段与较短部分的比例中项。欧多克斯发现这种线段之间的中外比例关系存在于许多图形中。最有趣的是，五星图中的每一条线段，都跟比它稍长的那条线段形成“中外比”。欧多克斯避免把无理数当作数，他不用数表达比。对于线段长度、角的大小及其他的量和量的比，都避免给予数值。因此，他没有给出“中外比”的数值。

文艺复兴时期的欧洲，由于绘画艺术的发展，促进了对“奇妙分割”的研究。当时，出现了好几位身兼几何学家的画家，著名的有帕奇欧里、丢勒、达·芬奇等人。他们把几何学上图形的定量分析用到一般的绘画艺术，从而给绘画艺术确立了科学的理论基础。

1525年丢勒制定了一种绘图的比例法则，其间揭示了中外比在绘画中的重要地位。丢勒认为，在所有矩形中，短边与长边满足中外比的矩形最美观。因为这样的矩形，“以短边为边，在这个矩形中分出一个正方形后，余下的矩形与原来的矩形相似，仍是一个服从中外比的矩形”，这使人们产生一种“和谐”的感觉。帕奇欧里首先把“中外比”称为“神圣比例”。并在1509年出版的《神圣比例》一书中论述了它，中外比被披上了神秘的外衣。后来达·芬奇把欣赏的重点转到使线段构成中外比的分割，而不是中外比本身，提出了“黄金分割”这一名称。

黄金分割中的分点叫做“黄金分割点”。“中外比”又叫“黄金比”，从古希腊直到现在都有人认为这种比例在造型艺术中有美学价值。如工艺美术或日用品的长和宽的设计中常用这比例，舞台上的报幕员站在舞台宽度的黄金分割点的位置时最美观、最佳;古代的不少建筑物，其高与宽的比也是黄金比。在中世纪，黄金比被作为美的信条而统治着当时欧洲的建筑和艺术。

自从无理数被确认后，人们有可能给出黄金比的数值。

设AB=l，AP=a，则PB=l－a

∵

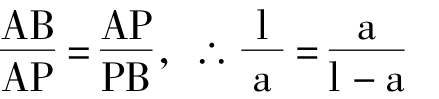
∴a³+al－l²=0

∴a=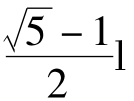(考虑到a＜l)

可见黄金比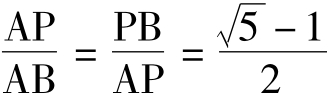。人们把这个数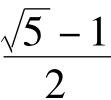叫做“黄金数”。前面我们已经看到黄金数与斐波那契数有关，它还与优选法有关。优选法中普遍常用的方法是0.618法，所谓0.618就是黄金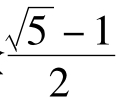的近似值，因此，0.618法也称为黄金分割法。

现代医学研究还表明，黄金比对人们自我保健有重要作用:人生存的最佳气温约23℃，它恰巧是正常体温(37℃)的0.618倍;吃饭最好只吃六、七成饱;摄入的饮食最好是“六分粗，四分精”;运动与静养的比例关系最好是“四分动，六分静”。