球体积的证明

球体积的证明

刘徽在注《九章算术》时，研究了球体积公式。在《九章算术》中，提出了V=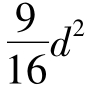的球体积计算公式。从这个公式可以看出，当时把足球的体积作为它的外切立方体体积的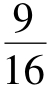倍来计算的，其中“9”实际表示π²，因那时人们经常取π=3进行计算。刘徽首先看出了其中的错误。他发现了一种有趣的立体图形，并把它叫做“牟合方盖”。牟，相等;盖，伞。“牟合方盖”是指两个半径相同，且两轴相互垂直相交的圆柱的公共部分。由于其形状就像把两个方口圆顶的伞对合在一起，故取名为“牟合方盖”。刘徽指出球体积应该等于外切于它的一个牟合方盖体积的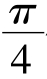倍，即

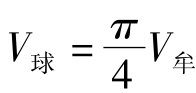
因此，计算球体积的问题归结为计算V牟的问题，但刘徽一直没有找到求“牟合方盖”的体积办法。他坦率地说:“欲陋形措意，惧失正理。敢不阙疑?以俟能言者。”希望后世能干的学者能尽快解决。

眼下暂且不谈后世学者的事，先讲讲读者关心的问题:刘徽是怎样想到这种有趣的图形的?有人说，因为他曾经长时期使用过一种方口圆顶的斗笠，从中受到启发。这种开玩笑的说法是没有根据的。数学史家推测，他是应用了类推法。

刘徽研究《九章算术》时曾发现:圆柱、圆锥、圆台的体积分别与同高的外切方柱、方椎、方台的体积之比，等于同高处横截面面积之比，即π∶4。刘徽认为，球体的体积可以通过其他容易求出体积的立体来表示，只要这个立体与球体在同高处的截面面积之比处处相等就可以了。

由于刘徽将球体看作是从圆柱到圆台这一变化过程的继续，因此所要寻找的立体，也应该是从方柱到方台这一变化过程的继续，而且它的截面既应是正方形的，又该与球同高处的截面——圆的面积之比恒为π∶4;这一立体应该是一个中心对称的，且对称中心截面面积为最大，而且截面分别向上、下逐渐缩小的立体。

另外，根据《九章算术》将球体放在外切圆柱及外切立方体之中考察的启发，刘徽醒悟到这立方体应该是内切于立方体的两个直交圆柱的所围部分，即“牟合方盖”了。

“牟合方盖”的发现是一个很了不起的成就，这反映了刘徽已经不是单纯地停留于经验总结，他已经采用了辩证的思维形式。

刘徽之后200多年，他所期望的“能言者”果真出现，那就是祖冲之和他的儿子祖繿(又名祖繿之)。祖繿也是博学多才的数学家，从小就懂得孝敬父母，勤奋学习。传说，在祖冲之临终的时候，祖繿发誓要继承发扬他父亲的成就，一定要让皇帝采纳《大明历》，还说每年祖繿总要给他父亲上坟，向他父亲的在天之灵汇报读书、研究心得。后来，他果真实现了自己的誓言。祖繿的主要工作是对《级术》进行修改、补充，有人还认为《级术》是由祖冲之和祖繿合著的。祖冲之在与戴法兴辩论时曾指出张衡盲从古人，沿用了《九章算术》中错误的球体积公式。看来，祖冲之已经得到了正确的球体积计算公式。但是唐朝李淳风在注《九章算术》时，又说所引用求球体积的方法是祖繿的。现在人们推测很可能是，祖冲之已经明确地知道以前的球体积公式是错误的，并且找到了正确的球体积公式，而祖繿则将它清晰地表达出来，并给出了严格的证明。

祖冲之、祖繿父子，运用“祖繿原理”获得球体积公式。所谓祖繿原理，是指“夹在两个平行平面间的两个立体，被平行于这两个平面的任何平面所截。如果它们的截面面积总相等，那么这两个立体的体积相等”。

西方数学书上称这一原理为“卡瓦列里定理”，他们认为是17世纪时意大利数学家卡瓦列里于1635年最早发现的。实际上，祖繿早于卡瓦列里1100多年前就发现了。

祖繿原理的原文是:“幂势既同，则积不容异。”按现在的话来说，即:二同高的立体，如在等高处的截面积相等则体积也相等。该文原载于祖冲之、祖繿父子撰写的《缀术》一书，《缀术》已失传。唐朝数学家李淳风作《九章算术》注时，把祖繿原理及祖繿的由球体积求直径的“开立圆术”引用了进去，这才使这一发明得以流传下来。

祖繿继承了刘徽未完成的事业，求出了“牟合方盖”的体积，从而得到球体积公式。他是这样做的:

取牟合方盖(简称“方盖”)的1/8，如图(a)，设圆柱半径为R。

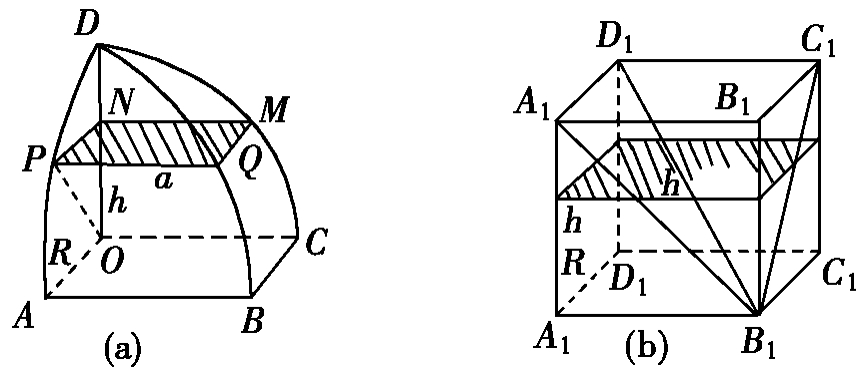
作一距底面h的平面交方盖，得一正方形PQMN(用阴影表示)，其边长为a，则有a²=R²－h²

另作一棱长为R的正方体，如图(b)，且使它的底面A₁B₁C₁D₁，与方盖的底ABCD在同一平面上。从正方体中挖去一个倒立的四棱锥，得到一个新几何体G。作一距底面为A的截面，交G得一曲尺形截面(图(b)中阴影表示)，其面积为R²－h²=a²。

由祖_繿原理，方盖的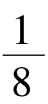与G等积，而G的体积=R³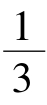－R²×R=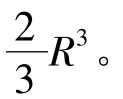

所以，牟合方盖的体积V_牟=8×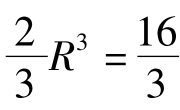R³。

再由刘徽的公式，即可求得:

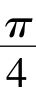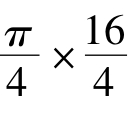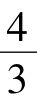V_球=V_牟=R³=πR³

这个球体积公式是数学史上的一个巨大成就，也是我们中华民族对世界科学的伟大贡献。

祖繿原理还可以推广为:“夹在两平行平面间的两个立体，被平行于这两个平面的任一平面所截，如果它们的截面面积的比恒为一定值，那么这两个立体的体积之比也等于这个定值。