第三节 万有引力定律的发现
惠更斯和胡克等人,对万有引力定律的发现做出了贡献,牛顿最后完成了万有引力定律的发现。
1.惠更斯发现了向心力定律
著名荷兰数学家、天文学家、物理学家惠更斯1629年生于海牙。他从小热爱数学,成绩卓著,法国大科学家笛卡儿在看到青年惠更斯的头两篇数学论文时,称赞他“前途无量”。惠更斯改进了望远镜物镜,发明了新的消色差目镜,用自制的望远镜发现了土星光环和第一颗卫星(土卫六),计算确定了土卫六运动周期。他最先判定地球两极附近是扁的,提出了用秒摆测定重力加速度的思想。
1656年惠更斯发明了摆钟。其后在研究碰撞实验中发现了速度的矢量性,进而认识到圆周运动中速度方向变化与加速度相联系。这种认识及对摆钟理论和一系列有关问题的研究,使他求得了摆的振动中心和振动周期,最先提出了向心力定律。
惠更斯在1673年发表的论文《摆钟》一文中,他将匀速圆周运动看作切线方向的匀速直线运动与指向圆心方向的匀加速运动的合成。如图1所示。
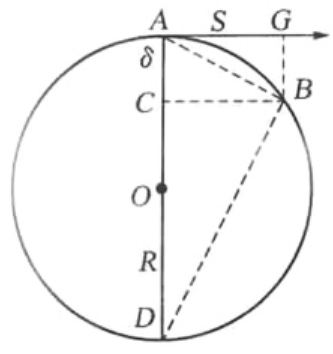
匀速圆周运动的合成
惠更斯对此作了简捷的证明。在极短的时问τ内,物体沿圆周运动通过弧长为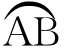 ,将
,将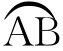 看作
看作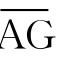 与
与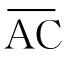 的合成,其中
的合成,其中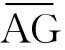 =S,为物体沿切线方向匀速直线运动的路程,AC=δ,为指向圆心的匀加速直线运动的路程。所以S=vτ,δ=aτ2/2,a=2δv2/S2。又由△AGB~△DCB得:S/δ=CD/S一(2R一δ)/S,所以S2=2Rδ-δ2。略去δ2。所以a=v2/R。这就是惠更斯得到的向心加速度公式。公式表明“两个等重的物体在大小不同的圆周上作等速运动,则该两物体的向心力之比等于两圆周直径的反比”。“两个等重的物体在大小相同的圆周上以不同速度各作匀速运动,则运动较快的物体的向心力与运动较慢的物体的向心力之比等于其速度的二次方之比。”
=S,为物体沿切线方向匀速直线运动的路程,AC=δ,为指向圆心的匀加速直线运动的路程。所以S=vτ,δ=aτ2/2,a=2δv2/S2。又由△AGB~△DCB得:S/δ=CD/S一(2R一δ)/S,所以S2=2Rδ-δ2。略去δ2。所以a=v2/R。这就是惠更斯得到的向心加速度公式。公式表明“两个等重的物体在大小不同的圆周上作等速运动,则该两物体的向心力之比等于两圆周直径的反比”。“两个等重的物体在大小相同的圆周上以不同速度各作匀速运动,则运动较快的物体的向心力与运动较慢的物体的向心力之比等于其速度的二次方之比。”
惠更斯的向心力定律,为探索推动行星绕日运动的力指明了正确方向,人们很自然地从行星的向心力中猜测到太阳对行星的吸引力,这就为万有引力定律的发现奠定了最后一块基石。惠更斯已接近于发现万有引力定律。
2.胡克、哈雷和雷恩的发现
1661年,英国皇家学会成立一个专门委员会研究重力问题。物理学家胡克、天文学家哈雷、建筑师雷恩在引力问题研究方面都作出了重要贡献。胡克觉察到引力和地球上物体的重力本质相同。1662和1664年,他试图找出物体的重量随离地心距离的变化关系,曾在高山上及矿井中做实验,未获成功。1674年,胡克提出了关于引力的三条假设:
第一,据我们在地球上的观察可知,一切天体都具有倾向其中心的吸引力,它不仅吸引其本身各部分,并且还吸引其作用范围内的其它天体。因此,不仅太阳和月亮对地球的形状和运动发生影响,而且地球对太阳和月亮同样也发生影响,连水星、金星、火星和木星对地球的运动都有影响。
第二,凡是正在作简单直线运动的任何天体,在没有受到其它作用力使其倾斜,并使其沿着椭圆轨道、圆周或复杂的曲线运动之前,它将继续保持直线运动不变。
第三,受到吸引力的物体,越靠近吸引中心,其吸引力也越大。至于此力在什么程度上依赖于距离的问题,在实验中还未解决。一旦知道了这一关系,天文学家就很容易解决天体运动的规律了。
这是在万有引力诞生前关于引力的最精辟的论述。
1679年底至l 680年初,牛顿在回答胡克问询的复信中,曾两次出现错误。胡克在纠正牛顿错误中明确指出,重力是按距离的二次方成反比变化的。这时,依据惠更斯的向心力定律从开普勒行星运动第三定律推出引力二次方反比关系的还有哈雷和雷思。
1684年1月在伦敦的一次聚会中,啥雷、雷恩和胡克谈论到二次方反比的力场中物体的运动轨迹问题。胡克声称,可以用二次方反比关系证明一切天体的运动规律。雷恩怀疑胡克的说法,提出如果有谁能在两个月内给出证明,他愿出40先令作为奖励。胡克坚持说他确能证明,只是不愿先公开,想看看有谁能解决,别人解决不了,他再公布自己的证明。胡克、哈雷、雷恩关于引力与距离二次方反比关系的发现,对牛顿很有启示。尤其是胡克将匀速圆周运动看作不平衡状态,认为有某种力持续地作用于物体,破坏了物体原有的匀速直线运动状态,使物体沿着闭合的圆形轨道运动,以及1679~1680年间的通信对牛顿有很大教益。从此后牛顿采用了惠更斯的“向心力”一词。
3.牛顿成功地发现了万有引力定律
杰出的英国物理学家、数学家、发明家牛顿,1642年生于英国林肯郡伍尔索普,是一个十足的农家孩子。小时候对机械发明很感兴趣。1 661年考入剑桥大学,博学多才的著名学者巴罗将牛顿引向自然科学的广阔天地。牛顿是一位“杰出的天才”、“有惊人的创造才能”,“他那几乎神一般的思维力,最先说明了行星的运动和图像、彗星的轨道和大海的潮汐”。是现代自然科学的奠基人,经典物理学的创始人,微积分的发明人之一,牛顿还发明了反射式望远镜。
由于胡克在引力问题上的矜持,1684年4月啥雷前往剑桥大学向牛顿请教:“假设一个行星受到太阳以和距离的二次方成反比递减的力的吸引,那它是以怎样的曲线运动呢?”牛顿马上回答“是椭圆”,并说自己作过计算。当哈雷表示希望看到计算内容时,牛顿称一时找不到。3个月后,牛顿将计算内容寄给了啥雷。这篇论文没有题目,后来人们通称为《论运动》。
文中讨论了在中心引力作用下物体运动轨迹的理论,由理论导出了开普勒行星运动三个定律,这是其成功之处。但牛顿对惯性和引力的认识存在错误和不足,他将物体具有的惯性称为“固有力”,将引力只看作重力,尚未认识到引力的普遍性。
经过8个多月的深入思考和严谨的数学推导,牛顿写成了《论物体的运动》的长篇文章,交给了剑桥大学图书馆。这篇长文中,牛顿解决了对惯性的认识问题,承认圆周运动是匀加速运动,与匀加速直线运动有联系;牛顿证明了均匀球体对球外物体的吸引力与球的质量成正比,与从球心算起的球到物体间的距离二次方成反比,提出可以将均匀球体看成质量集中于球心的质点;吸引是相互的;把重力和引力统一起来,明确了引力的普遍性。
《论物体的运动》的第二部分,收集在1687年出版的《自然哲学的数学原理》一书中,标题是“论世界体系”。文中阐述了牛顿在伽利略研究抛射体运动规律的基础上想象出的理想实验:“行星依靠向心力可以保持在一定的轨道上。这只要考虑一下抛射体的运动,就可以很容易理解了:一块被抛出的石头,由于自身重量的压迫不得不离开直线路径,它本应按照开始的抛射方向走直线,而现在它在空中划出的却是一条曲线,最后落到了地面;抛射时的速度越大,它在落地时就走得越远。因此,我们可以假定抛射的速度不断增大,使它到达地面之前能划出l、2、5、10、100、1000英里长的弧线,最后一直增加到超出了地球的界限,这时石头就要进入空间而碰不到地球了。”如图2所示。图中,物体自V点抛射,当抛射速度依次增大时,物体划出的弧线越来越长,即 <
<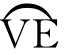 <
< <
<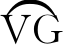 ,直至形成圆周VBAV。若V点高度依次增加,则可得一些与地球同心或偏心的圆圈。
,直至形成圆周VBAV。若V点高度依次增加,则可得一些与地球同心或偏心的圆圈。
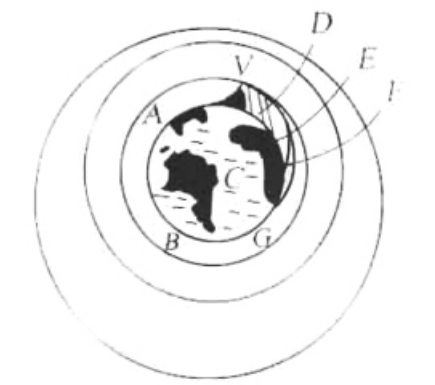
2 牛顿抛射体理想实验
牛顿从其中领悟到,石头下落与天体运动有一个共同的原因——引力,从而将地球上物体运动与天体运动统一起来。牛顿认为:惯性是原子普遍具有的固有属性,用它可以量度质量的多少,称为惯性质量;引力也是原子的普遍属性,是物质间存在相互作用的一种性质,引力质量与惯性质量是统一的。
牛顿以空前的洞察力、突破性的思辨和辛勤的劳动换取了丰硕的科学成果,发现了万有引力定律:F=Gm1m2/r2。其中m1,m2分别为两个物体的质量,r为它们间的距离,G为万有引力常数。为了更加稳妥,他以月球为例,用运动学与动力学两种方法计算了月球的向心加速度,差值很小,并且可以归结为月球绕地球运转轨道并非理想圆形等因素。完全可以说,这种对万有引力定律的检验方法取得了令人满意的结果:万有引力定律是正确的。
万有引力常数G,是一个非常重要的物理常数,它是经典力学时代的标志。1798年,英国物理学家卡文迪什用扭摆实验测得了G值,G=6.7×101 1米3·秒-2·千克-1,最后完善了万有引力定律。
4.万有引力定律获得了震撼世界的成功
牛顿用经验归纳法和科学的推理方法将前人获得的优秀科学成果加以分析、综合、升华,发现了万有引力定律,创立了经典力学。也可以说,他是“站在巨人的肩上”发挥聪明才智,并以惊人的创造力和想象力获得这一具有划时代意义的巨大科学成就的。
万有引力定律发现前后,人们对彗星的出现很不理解。天文学家哈雷注意到1531年、1607年、1682年出现的3颗彗星轨道基本重合,推想这3颗可能是同一颗彗星出现3次的结果,周期为76年。他依万有引力定律计算出这颗彗星的扁长椭圆轨道,并预言它将在1758年再次出现。人们果然在1759年初观测到了这颗彗星,事件轰动了整个欧洲,万有引力定律获得了很大成功。
人们将这颗星定名为“哈雷彗星”。1798年,英国科学家卡文迪什测得了万有引力常数G,并计算了地球的质量M=6×102 4kg,取得了“称量地球”的轰动效果,这说明了万有引力定律是正确的,有难以估量的功能。
1801年,皮阿齐在西西里岛用眼发现了第一颗小行星——谷神星,后来丢失了。德国物理学家、天文学家高斯准确地计算了谷神星的轨道后,人们又找到了它。1830年,高斯按万有引力定律考虑到木星对它的摄动,将其轨道计算得更为精确,为人们对它的研究提供了很大方便。太阳系第八大行星——海王星、第九大行星——冥王星的发现,都应归功于万有引力定律。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















