输给数码相机的手动相机

输给数码相机的手动相机

F值的秘密

现在，随着数码相机的流行，手动相机显得像古董似的，但是拍摄作品时它依然受到人们的青睐。使用手动相机进行拍照的时候，根据天气的好坏需要对准焦距来调整光量。根据一般的摄影常识，晴天将F值调大到11或16，而在阴天需调小到4或5.6。

在手动相机镜头的外围标有的F值是1.4，2，2.8，4，5.6，8，11。乍一看，F值好像都是些没有规律的数字。其实，这些数字是有规律的。第一个F值1.4是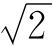的近似值，第二个值2是乘两个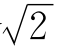的近似值，而第三个值2.8是乘三个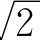的近似值。那么，这样用无理数的成倍数来规定F值的理由是什么呢？

F值是利用“镜头的焦点÷光圈口径”来计算的，因为镜头的焦距是一定的，所以F值与光圈口径的大小成反比。例如，晴天因为需要少量的光线，所以应该调小光圈口径。从而成反比关系的F值就变大了。

另外，在阴天需要按2倍的量增加光线时，应该按2倍的量调大光圈。但是，圆的面积是πR²（圆周率半径的平方），所以为了按2倍增加光圈的大小，必须将半径调大为√2倍。

无理数——希勃索斯的良心宣言

在相机光圈的数据中经常使用的无理数是由古希腊带有传奇色彩的数学家团体毕达哥拉斯学派发现的。众所周知，这个世界是由数字组成的，这就是毕达哥拉斯学派的价值观。而且他们坚信，所有的数是可以通过两个数的协调比来表示的“有理数（rational number）”。

非常可笑的是，根据毕达哥拉斯学派的非常著名的理论之一的毕达哥拉斯定理，发现了无法用两个数的比来表示的“无理数（irrational number）”。毕达哥拉斯学派认为这一发现将动摇他们在学术界的统治地位，所以没有把无理数的存在公布于世。但是，毕达哥拉斯学派中的一员希勃索斯凭自己的良心宣布了这个世界除了有理数还存在无理数的事实。

结果，希勃索斯招来了毕达哥拉斯学派的反感，受到百般折磨，最后竟遭到沉舟身亡的惩处。没能以宽广的胸襟接受这一新的数学领域的发现的毕达哥拉斯学派受到人们的谴责是不可避免的，但是其纯洁的信仰和坚定的价值观在现今时代是很少见的。